Ch ng ươ
Sư canh tranh trong hoat
đông san xuât kinh doanh
luôn đoi hoi cac nha quan ly
doanh nghiêp phai thương
xuyên lưa chon phương an
đê đưa ra cac quyêt đinh
nhanh chong, chinh xac va
kip thơi vơi như!ng rang
buôc va han chê vê cac điêu
kiên liên quan tơi tiêm năng
cua doanh nghiêp, điêu kiên
Trong môn hoc Toa n kinh tê viêc giai ba i toa n
QHTT th ng đc th c hiên băng thuât toa n đn ươ ươ ư ơ
hi nh. Trong phân mêm Excel ba i toa n QHTT đc ươ
giai nhanh cho ng qua công cu ca i thêm la Solver.
6.1. M T S VÍ D V BÀI Ộ Ố Ụ Ề
TOÁN QHTTT
1. Bài toán lâp kê hoach sản xuất:
Môt xi nghiêp d đinh san xuât hai loai san phâm la ư
S1 va S2 t v t li u V1 và V2. S li u đc cho ừ ậ ệ ố ệ ượ ở
b ng sau:ả
Hoi xi nghiêp nên san xuât bao nhiêu đn vi san ơ
Mô hi nh toa n h c ọ. Goi x1, x2 lân l t la sô đn ươ ơ
vi san phâm S1, S2 cân san xuât.
Tông thu nhâp cua xi nghiêp ( cân la m c c đai ư ) se
la
f = 50x1 + 30x2 (nga n đô ng ).
Vây ba i toa n đăt ra đc pha t biêu tha nh: Ti m ca c ươ
biên sô x1 va x2 sao cho
f = 50x1 + 30x2 max,
v i ca c điêu kiên ơ
4x1 + 3x2 1.200,
5x1 + 2x2 1.080, (1.1)
x1 0, x2 0.
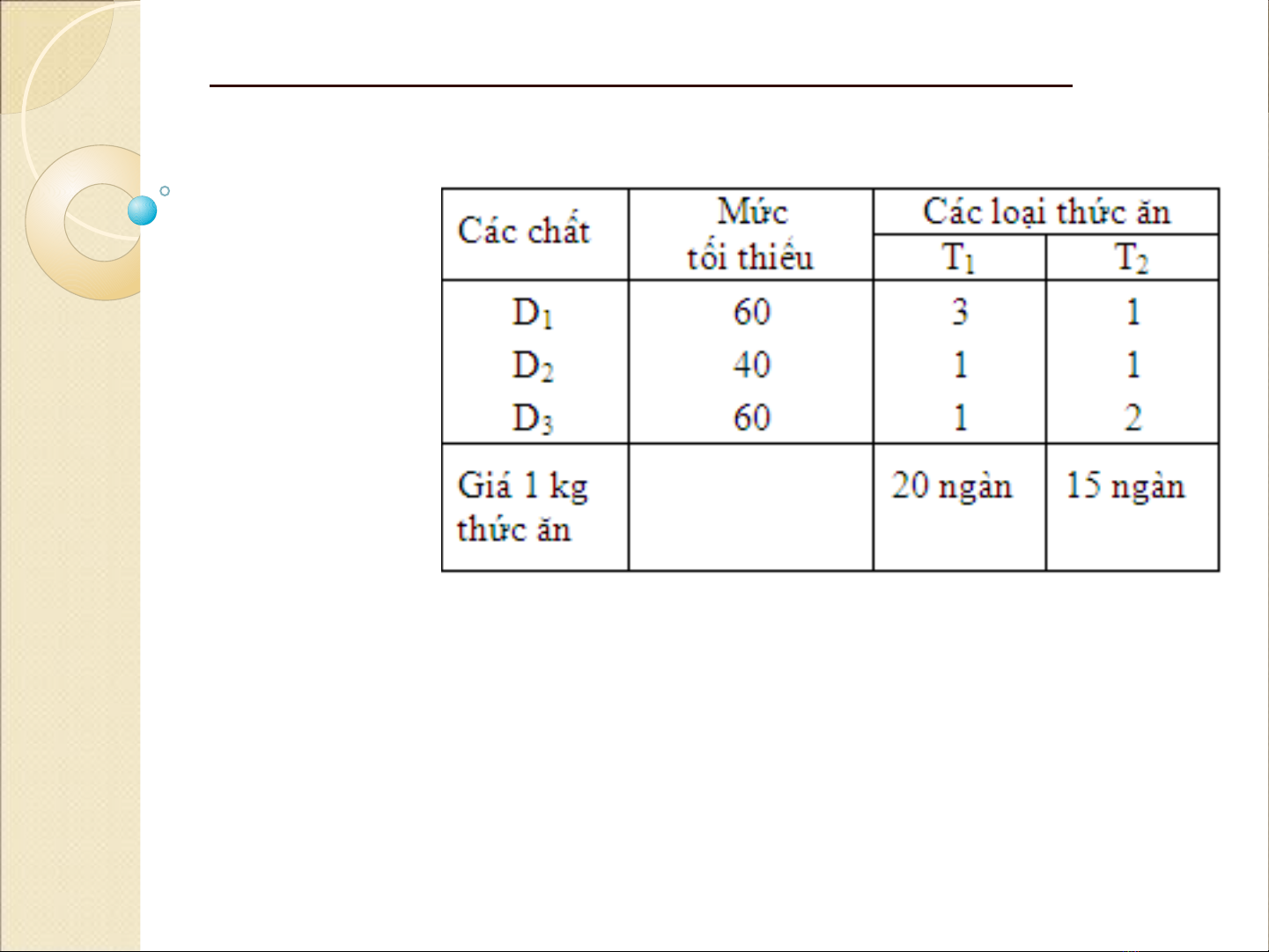
2. Bài toán xác định khẩu phần thức ăn
Kh u ph n th c ăn/ 1 b a ăn c a m t xi nghiêp ẩ ầ ứ ữ ủ ộ
chăn nuôi nh sau:ư
Hoi xi nghiêp cân mua bao nhiêu kg T1, T2 cho
môi b a ăn, sao cho v a đam bao tôt dinh d ng ư ư ươ
cho b a ăn cua gia su c, v a đê tông sô tiên chi ư ư
mua th c ăn la nho nhât? ư
Mô hi nh toa n hoc. Goi x1, x2 lân l t la sô kg ươ
th c ăn T1, T2 cân mua cho môi b a ăn. ư ư
Sô tiên chi mua th c ăn ( ưcân la m c c tiêu ư ) băng
f = 20x1 + 15x2 (nga n đô ng ).
Vây ba i toa n nêu trên đc pha t biêu tha nh: Ti m ươ
ca c biên sô x1 va x2 sao cho:
f = 20x1 + 15x2 min,
v i ca c điêu kiên ơ
3x1+ x2 60,
x1 + x2 40, (1.2)
x1 + 2x2 60,
x1 0, x2 0.