Bài giảng Vi mạch số
Biên soạn Ngô Văn Bình
Trang 1
Phần 1: Thiết kế hệ logic tổ hợp
I. Giới thiệu chung
Về cơ bản hệ điều khiển logic được chia làm 2 loại lớn:
- Hệ tổ hợp.
- Hệ tuần tư.
Trong hệ tổ hợp đầu ra tại một thời điểm bất kỳ chỉ phụ thuộc vào trạng thái các đầu
vào tại thời điểm đó, nghĩa là không có phần tử nhớ trong mạch, đối với hệ tuần tự thì
khác: Trạng thái ngỏ ra tại thời điểm đang xét không những phụ thuộc trạng thái vào tại
cùng thời điểm mà còn phụ thuộc vào trạng thái vào trong quá khứ có nghĩa là phải có
phần tử nhớ trong mạch.
Một hệ logic tuần tự có thể chứa các hệ logic tổ hợp con, những dử liệu thiết kế hệ tổ
hợp có thể được cho dưới dạng:
- Một tập hợp các mệnh đề.
- Biểu thức Boole.
- Bảng sự thật.
Nếu biết một cách biểu diễn có thể suy ra cách biểu diễn khác, như trong các lĩnh vực
thiết kế kỹ thuật khác số lượng thiết bị xử dụng cần phải nhỏ nhất để giãm chi phí, kích
thước, tiết kiệm năng lượng và tăng độ tin cậy. Các phương pháp để đạt được sự thực hiện
hàm Boole một cách đơn giản nhất còn phụ thuộc vào nhiều yếu tố.
Một cách đo độ phức tạp của hàm Boole là đếm số lượng "literal" tức số lượng chữ
có trong biểu thức Boole, literal sẻ xác định lượng dây nối và số lượng đầu vào của mạch
vì vậy cần phải giãm số lượng literal.
Một vấn đề khác là số lượng cổng cần thiết chính điều này quyết định kích thước của
mạch, một thiết kế đơn giản nhất là dùng ít cổng nhất chứ không phải ít literal.
Yếu tố thứ ba là số mức logic, giãm số mức logic sẻ làm giãm thời gian trể vì tín
hiệu đi qua ít cổng hơn nhưng nếu chỉ chú ý đến thời gian thì có thể lại làm cho số lượng
cổng tăng lên.
Trong phần này trình bày cách thiết kế một hệ tổ hợp để thực hiện mạch logic hai
mức, cách dùng các vi mạch có trong thực tế cho đến cách tổng hợp logic nhiều mức để
đạt được số lượng cổng cần dùng là ít nhất.
II. Quy trình thiết kế
Quy trình thiết kế thường được thực hiện theo một số bước sau đây:
- Phân tích yêu cầu và xác định tín hiệu vào - ra.
- Xác định bảng trạng thái và bảng sự thật.
- Đơn giản hóa.
- Viết phương trình tổng của tích hoặc tích của tổng.
- Vẽ sơ đồ AND - OR hoặc OR - AND.
- Biến đổi sang sơ đồ vi mạch thông dụng.
- Chọn linh kiện và ráp mạch.
Ví dụ:
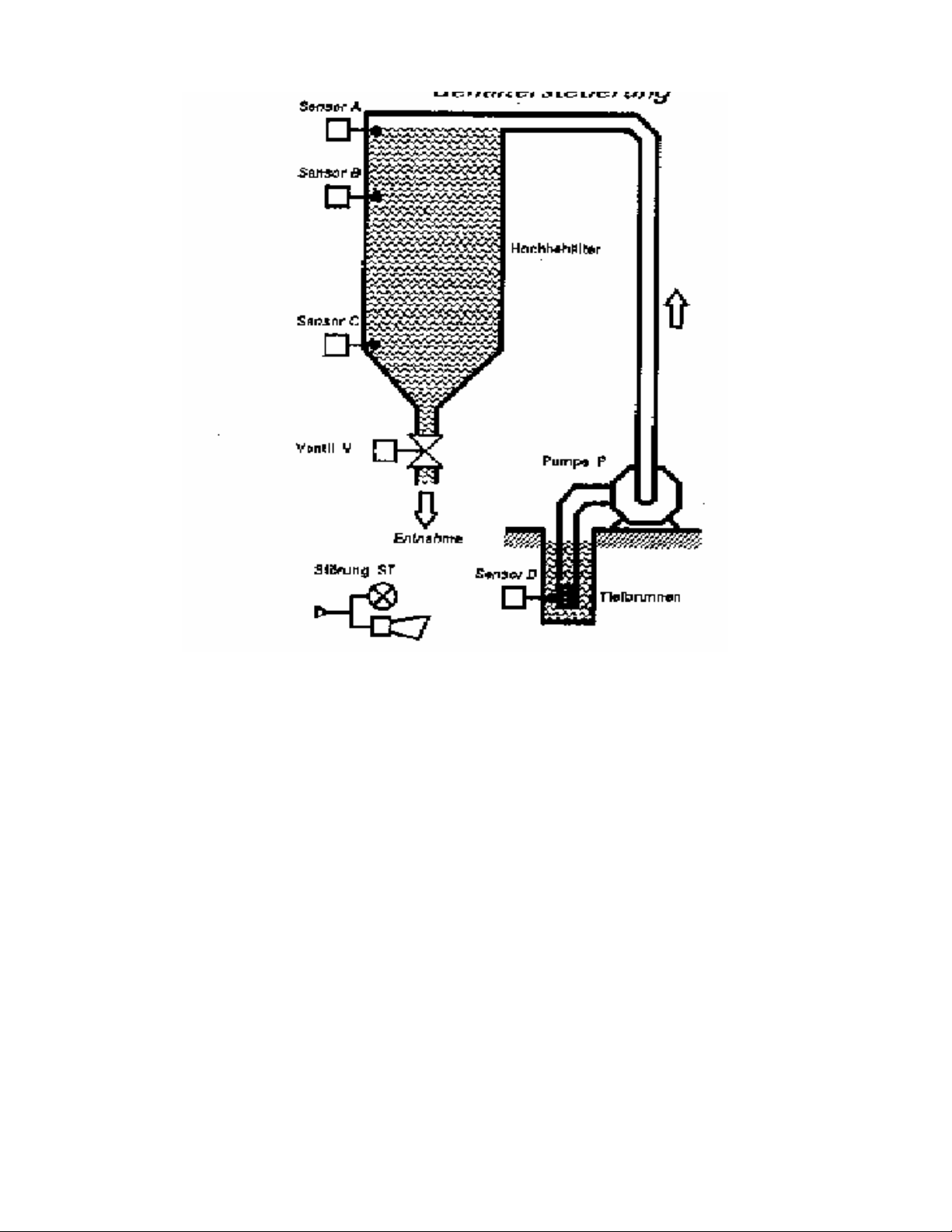
Thiết kế mạch logic điều khiển một bồn chứa nước với sơ đồ công nghệ và yêu cầu
như sau:
Bài giảng Vi mạch số
Biên soạn Ngô Văn Bình
Trang 2
- Bơm P chỉ chạy khi giếng đầy nước ( cãm biến D tác động) và bồn chưa đầy (cãm
biến A không tác động).
- Van V bình thường luôn luôn mở để sẳn sàng cung cấp nước và chỉ đóng lại khi
giếng hết nước và đồng thời bồn cũng cạn nước (cãm biến C không tác động) để giử lại
một lượng nước an toàn.
- Còi hoặc đèn báo động sáng khi hệ thống bị sự cố (A tác động nhưng C lại không
tác động).
Giải
1. Phân tích yêu cầu và xác định tín hiệu vào - ra
Từ sơ đồ công nghệ và yêu cầu điều khiển suy ra tín hiệu vào là: cãm biến A, C và
D (để đơn giản xem như không có cãm biến B) và tín hiệu ra gồm: bơm P, van V và đèn
BD
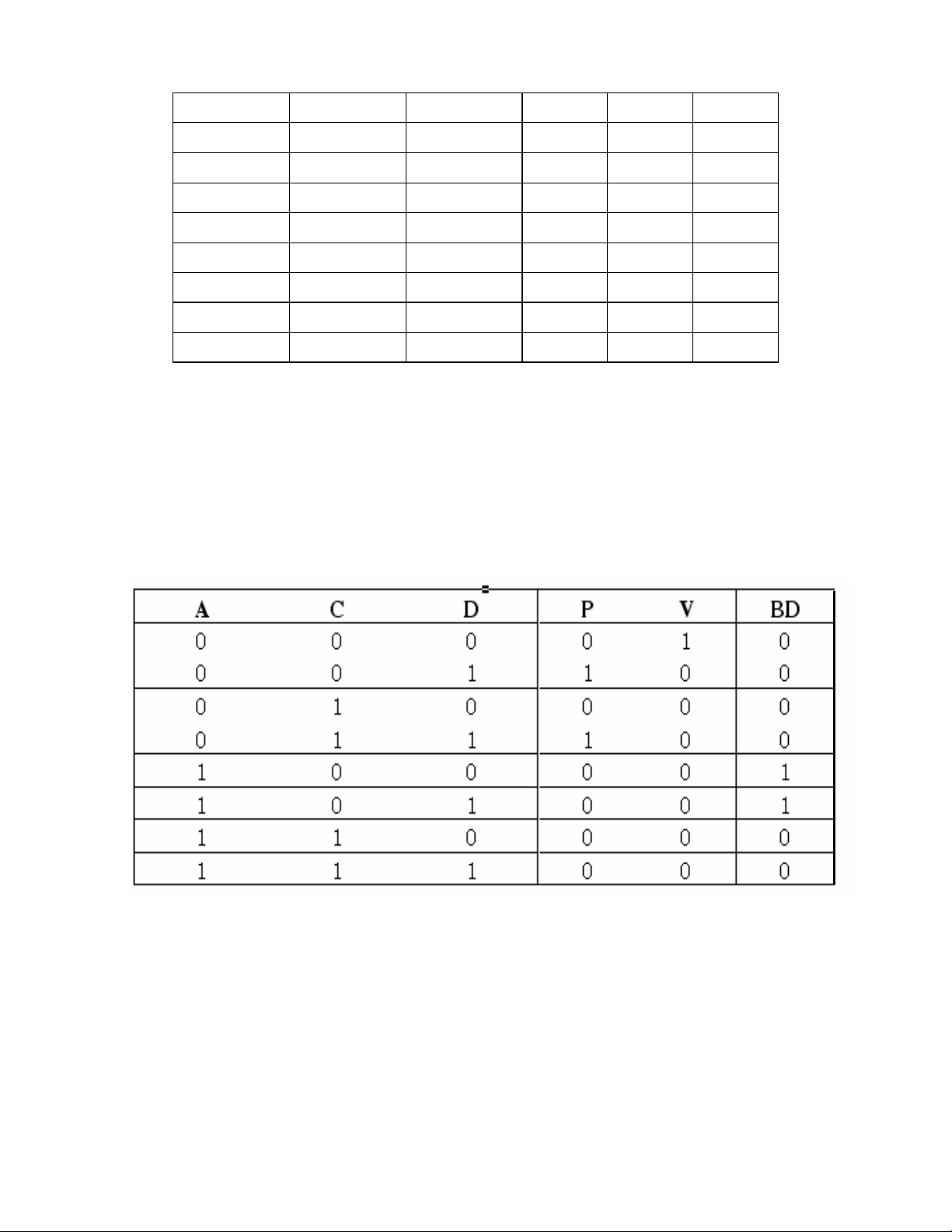
2. Xác định bảng trạng thái và bảng sự thật.
Bảng trạng thái là một dạng diển tả khác của yêu cầu điều khiển nội dung của bảng
sẽ cho biết quan hệ giữa tín hiệu ra với tín hiệu vào.
Bài giảng Vi mạch số
Biên soạn Ngô Văn Bình
Trang 3
A C D P V BD
K.taùc ñoäng K.taùc ñoäng K.taùc ñoäng Döøng Ñoùng Toái
K.taùc ñoäng K.taùc ñoäng Taùc ñoäng Chaïy Môû Toái
K.taùc ñoäng Taùc ñoäng K.taùc ñoäng Döøng Môû Toái
K.taùc ñoäng Taùc ñoäng Taùc ñoäng Chaïy Môû Toái
Taùc ñoäng K.taùc ñoäng K.taùc ñoäng Döøng Môû Saùng
Taùc ñoäng K.taùc ñoäng Taùc ñoäng Döøng Môû Saùng
Taùc ñoäng Taùc ñoäng K.taùc ñoäng Döøng Môû Toái
Taùc ñoäng Taùc ñoäng Taùc ñoäng Döøng Môû Toái
Bảng sự thật là bảng trạng thái khi thay vào đó các giá trị logic tương ứng 0 và 1. Do
đó từ một bảng trạng thái có thể dẫn đến nhiếu bảng sự thật khác nhau tùy theo hệ thống
thực tế. Trong trường hợp này có thể quy định như sau:
Với các cãm biến: Tác động tương đương với 1 và không tác động là 0
Bơm P chạy là 1 và dừng là 0.
Van đóng là 1 và mở là 0.
Đèn BD sáng là 1 và tối l.à 0.
Suy ra bảng sự thật như sau.
Hình 1.3 Bảng sự thật
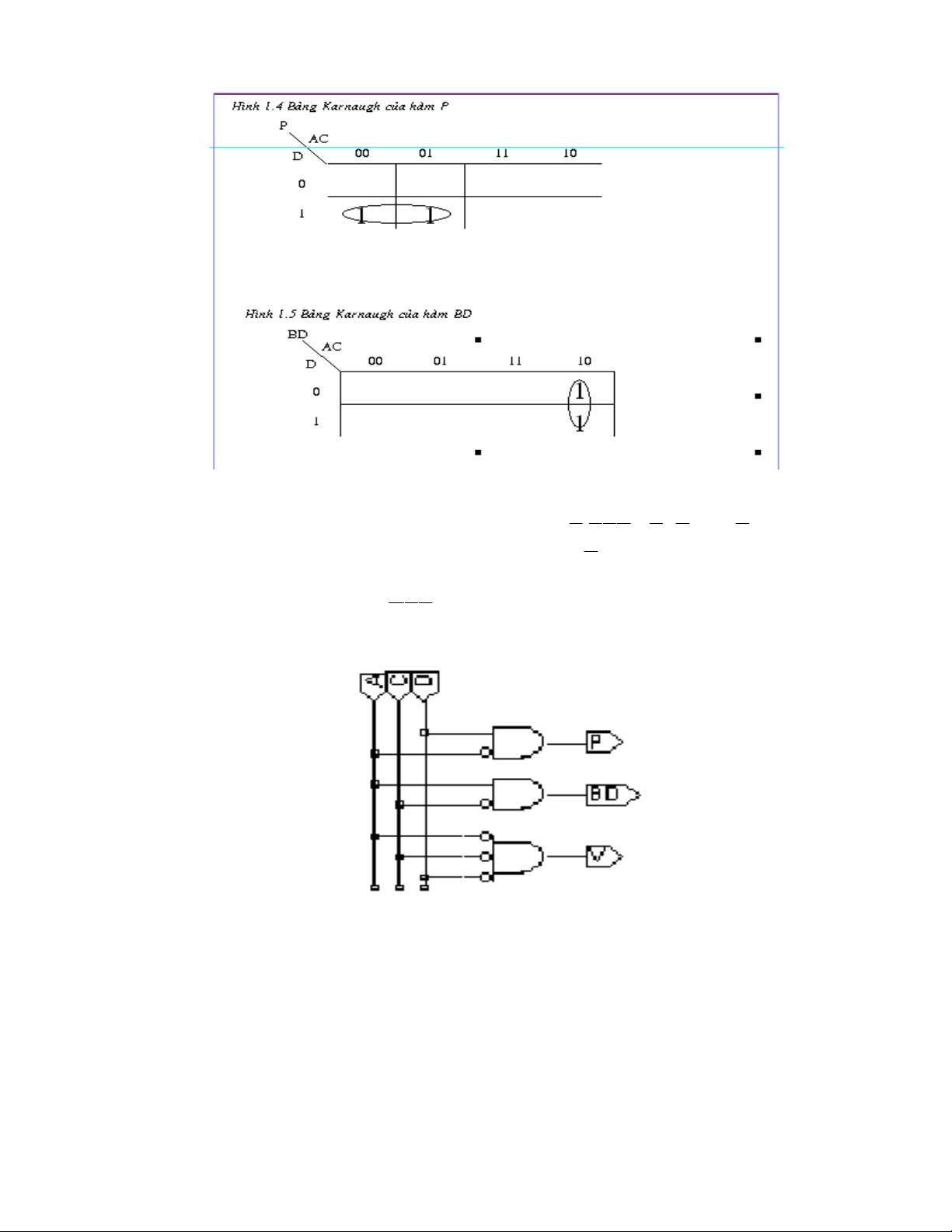
3. Đơn giản hóa
Quá trình đơn giản có thể thực hiện bằng bảng Karnaugh hoặc đại số logic, bảng
Karnaugh là một phương pháp đồ thị, trực quan , dể hiểu và thường được áp dụng trong
trường hợp số lượng ngỏ vào không nhiều lắm.
Hình 1.4 Bảng Karnaugh của hàm P
Bài giảng Vi mạch số
Biên soạn Ngô Văn Bình
Trang 4
4/ Viết phương trình tổng của tích hoặc tích của tổng
Phương trình đơn giản của hàm P: P =
D A
ABC ABC ABC ABC
Phương trình đơn giản của hàm BD: BD =
AC
Riêng hàm V chỉ có một trường hợp bằng 1 nên không cần đơn giản
V =
D AC
5/ Vẽ sơ đồ AND - OR hoặc OR - AND
Hình 1.6 Sơ đồ mạch dạng AND - OR
Số vi mạch cần dùng để thực hiện sơ đồ AND - OR
7404 - 6 đảo
7408 - 4 AND 2 input
7411 - 3 AND 3 input
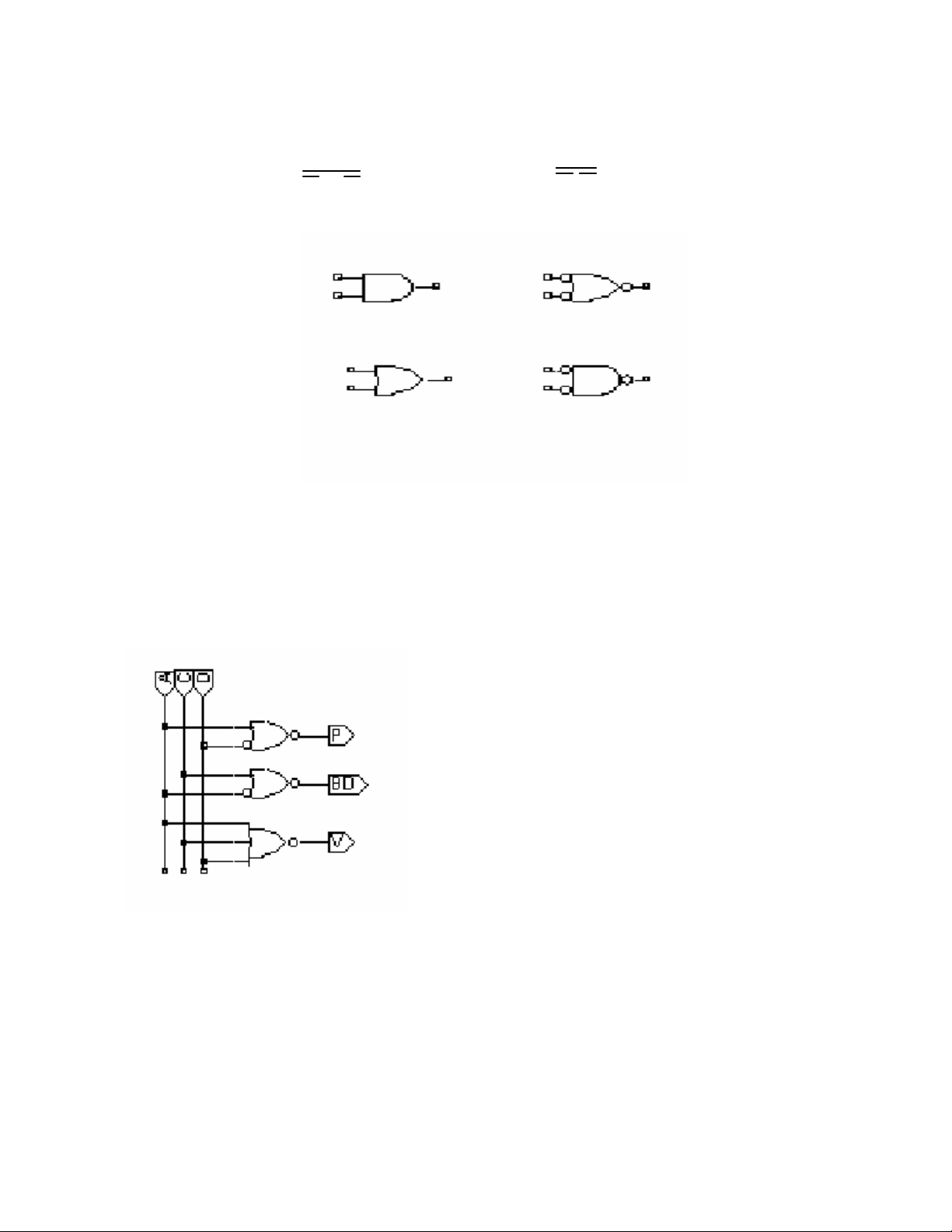
6/ Biến đổi sang sơ đồ vi mạch thông dụng
Trong công nghệ vi mạch việc thực hiện bằng các cổng NAND và NOR là hiệu
quả hơn. Trong thực tế, các cổng AND và OR được thay thế bằng các cổng NAND và
Bài giảng Vi mạch số
Biên soạn Ngô Văn Bình
Trang 5
NOR với một bộ đảo được đặt thêm ở phía sau. Ngoài ra một hàm logic bất kỳ gồm có
AND, OR và NOT có thể được thực hiện bằng cách chỉ dùng các cổng NAND hoăc NOR.
Sự chuyển đổi này dựa trên định lý De Morgan
AB A B
.
A B AB
Hình 1.7 Kết quả của định lý De Morgan
Một cổng AND tương đương một cổng NOR với tất cả các ngỏ vào đảo, và một
cổng OR tương đương một cổng NAND với tất cả các ngỏ vào đảo. Từ những nguyên tắc
vừa trình bày sơ đồ hai mức logic AND - OR được chuyển thành dạng NOR - NOR như
sau:
Hình 1.8 Sơ đồ mạch dạng NOR
Số vi mạch cần dùng
7402 - 4 NOR 2 input
7427 - 3 NOR 3 input
III. Vi mạch phức hợp
Như đã biết, mạch logic nhiều mức có thể được thực hiện bằng cách ghép các cổng
rời, trong công nghệ TTL cũng như CMOS có chế tạo sẳn một số vi mạch nhiều mức logic
đơn giản , đó là các cổng phức hợp AOI (AND - OR - INVERT) hoặc OAI (OR - AND -
INVERT) nhiều đầu vào
Một khối AOI là một mạch logic ba mức bao gồm các cổng AND ở mức thứ nhất,
một cổng OR ở mức thứ hai và một cổng đảo ở đầu ra. Tương tự một khối OAI gồm các
cổng OR ở mức thứ nhất, một cổng AND ở mức thứ hai và một cổng đảo ở đầu ra. Tóm lại