www.ptit.edu.vn Trang 1
X LÝ TÍN HI U SỬ Ệ Ố
H C VI N CÔNG NGH B U CHÍNH VI N THÔNG Ọ Ệ Ệ Ư Ễ
BÀI GI NG MÔNẢ
X LÝ TÍN HI U SỬ Ệ Ố
Gi ng viên: ảTS. Đ ng Hoài B cặ ắ
Đi n tho i/E-mail:ệ ạ 84-4- 3351 9391
B môn: ộKTĐT-Khoa KTĐT
H c kỳ/Năm biên so n: Kỳ 1/2009ọ ạ
www.ptit.edu.vn Trang 2
X LÝ TÍN HI U SỬ Ệ Ố
M đ uở ầ
•Tín hi u là khái ni m ch ra các bi n có mang ho c ch a m t lo i ệ ệ ỉ ế ặ ứ ộ ạ
thông tin nào đ y mà ta có th bi n đ i, hi n th , gia công ch ng ấ ể ế ổ ệ ị ẳ
h n nh : ti ng nói, tín hi u sinh h c (đi n tim, đi n não đ ), âm ạ ư ế ệ ọ ệ ệ ồ
thanh, hình nh, tín hi u radar, sonar...ả ệ
•Tín hi u s là tín hi u đ c bi u di n b ng dãy s theo bi n r i ệ ố ệ ượ ể ễ ằ ố ế ờ
r c. ạ
•X lý tín hi u s (DSP: Digital Signal Processing) là môn h c đ ử ệ ố ọ ề
c p đ n các phép x lý các dãy s đ có đ c các thông tin c n ậ ế ử ố ể ượ ầ
thi t nh phân tích, t ng h p mã hoá, bi n đ i tín hi u sang ế ư ổ ợ ế ổ ệ
d ng m i phù h p v i h th ng. ạ ớ ợ ớ ệ ố
•Các phép x lý tín hi u s c b n bao g m:ử ệ ố ơ ả ồ
–Phép ch pậ
–T ng quanươ
–L c sọ ố
–Các phép bi n đ i r i r cế ổ ờ ạ
–Đi u chề ế
www.ptit.edu.vn Trang 3
X LÝ TÍN HI U SỬ Ệ Ố
M đ u (tt)ở ầ
•Các c s toán h c v x lý tín hi u s đã có t th k 17 và 18,(bi n đ i ơ ở ọ ề ử ệ ố ừ ế ỷ ế ổ
Fourier) nh ng đ n th p niên 80 c a th k 20, cùng v i s ra đ i c a vi ư ế ậ ủ ế ỷ ớ ự ờ ủ
m ch tích h p c l n VLSI, các chíp dùng cho x lý tín hi u s ra đ i nh ạ ợ ỡ ớ ử ệ ố ờ ư
TMS 320 c a hãng Texas Instrument đã làm cho k thu t x lý tín hi u s ủ ỹ ậ ử ệ ố
b c sang m t b c ngo t m i phát tri n r c r .ướ ộ ướ ặ ớ ể ự ỡ
•Hi n nay, x lý tín hi u s đã có m t ph m vi ng d ng r ng rãi trong các ệ ử ệ ố ộ ạ ứ ụ ộ
lĩnh v c nh : x lý nh (m t ng i máy), đo l ng đi u khi n, x lý ti ng ự ư ử ả ắ ườ ườ ề ể ử ế
nói/âm thanh, quân s (b o m t, x lý tín hi u radar, sonar), đi n t y sinh ự ả ậ ử ệ ệ ử
và đ c bi t là trong vi n thông và công ngh thông tin.ặ ệ ễ ệ
•So v i x lý tín hi u t ng t , x lý tin hi u s có nhi u u đi m nh sau:ớ ử ệ ươ ự ử ệ ố ề ư ể ư
–Đ chính xác cao.ộ
–Sao chép trung th c, tin c y.ự ậ
–Tính b n v ng: không ch u nh h ng nhi u c a nhi t đ hay th i ề ữ ị ả ưở ề ủ ệ ộ ờ
gian
–Linh ho t và m m d o: Ch c n thay đ i theo ph n m m ta có th có ạ ề ẻ ỉ ầ ổ ầ ề ể
các tính năng ph n c ng thay đ i theo.ầ ứ ổ
–Th i gian thi t k nhanh. ờ ế ế
–Các chip DSP ngày càng hoàn thi n và có đ tích h p cao.ệ ộ ợ
www.ptit.edu.vn Trang 4
X LÝ TÍN HI U SỬ Ệ Ố
M đ u (tt)ở ầ
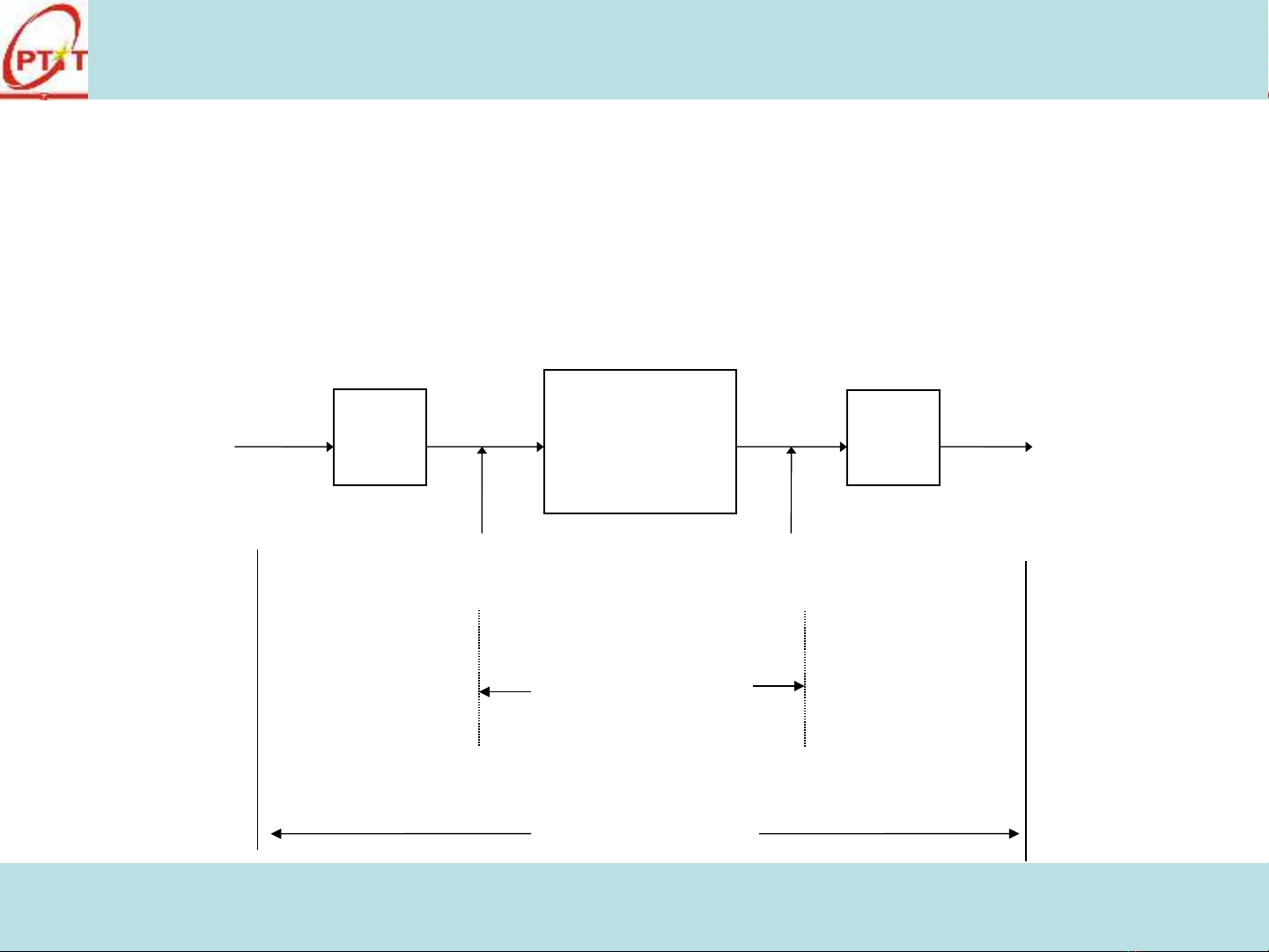
•Hình v sau mô t m t quá trình x lý tín hi u đi n hình và ta có th phân ẽ ả ộ ử ệ ể ể
bi t các khái ni m “X lý tín hi u s ” và “X lý s tín hi u”:ệ ệ ử ệ ố ử ố ệ
A/D D/A
B x lý sộ ử ố
DSP
Tín hi u sệ ố
Tín hi u ệ
tương tự
Tín hi u ệ
tng tươ ự
Tín hi u sệ ố
X lý tín hi u sử ệ ố
X lý s tín hi u ử ố ệ
www.ptit.edu.vn Trang 5
X LÝ TÍN HI U SỬ Ệ Ố
CH NG IƯƠ
Bi u di n tín hi u và h th ng r i r c ể ễ ệ ệ ố ờ ạ
trong mi n th i gian r i r c nề ờ ờ ạ