§¹i häc ®µ n½ng
Tr−êng ®¹i häc B¸ch KHOA
khoa s− ph¹m kü thuËt
-------¶ ·-------
bµi tËp c¬ häc ®¹i c−¬ng (MÐcanique gÐnÐrale)
c¬ häc ®¹i c−¬ng – dao ®éng vµ sãng c¬
dïng cho sinh viªn ch−¬ng tr×nh ®µo t¹o kü s− chÊt l−îng cao
(L¦U HµNH NéI Bé)
Biªn so¹n :
L£ CUNG – khoa s− ph¹m kü thuËt
®µ n¨ng 2006
Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
PHÁÖN I :
BAÌI TÁÛP CÅ HOÜC VÁÛT RÀÕN
2
Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
BAÌI TÁÛP CHÆÅNG ÄN TÁÛP :
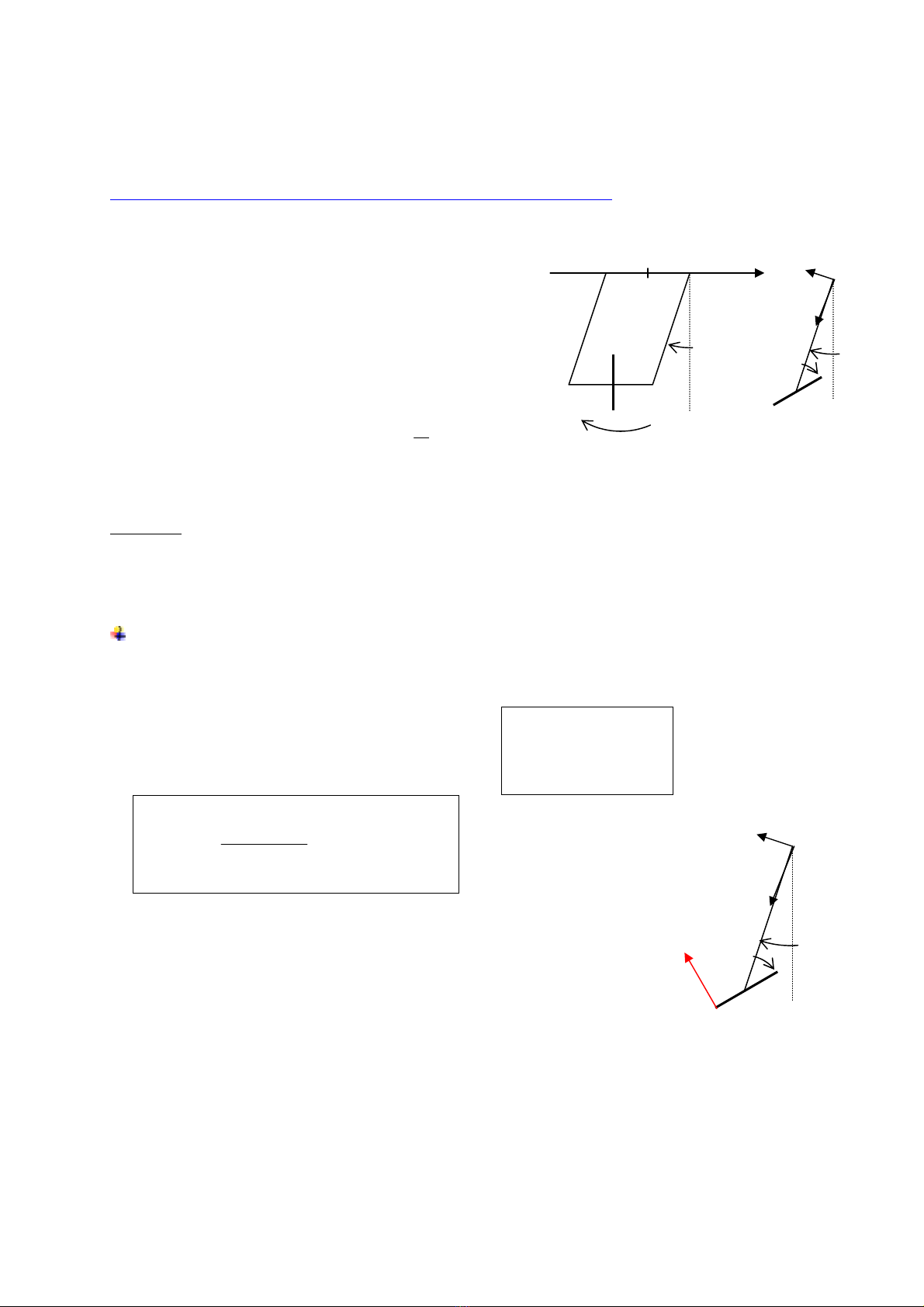
@ AÏp duûng 1 (Trang 11) : Chuyãøn âäüng cuía ngæåìi chåi xaì treo:
Mäüt xaì treo ABCD thæûc hiãûn caïcc dao âäüng hçnh sin
0.sin t
θ
θω
=. Ngæåìi chåi xaì treo tæång tæû nhæ mäüt
thanh TMP, quay xung quanh BC våïi váûn täúc goïc
tæång âäúi
ω
khäng âäøi so våïi xaì treo. Vaìo thåìi âiãøm
ban âáöu, ngæåìi chåi xaì treo åí tæ thãú thàóng âæïng, âáöu T
hæåïng lãn trãn.
Xaïc âënh gia täúc trong hãû quy chiãúu R2 gàõn liãön våïi xaì
treo, gia täúc Coriolis, gia täúc theo vaì gia täúc trong hãû
quy chiãúu traïi âáút R1 taûi thåìi âiãøm t
π
ω
=
cuía âiãøm P
(chán cuía ngæåìi choi xaì treo).
Cho biãút: OM = AB = DC = b; MP = d.
Baìi giaíi :
Gia täúc âiãøm P trong hãû quy chiãúu R2 :
Hãû quy chiãúu 2(, , , )
rz
R
Oe e e
θ
GGG gàõn liãön våïi âu chuyãøn âäüng quay quanh truûc cäú âënh trong hãû
quy chiãúu traïi âáút R1.
Trong R2, âiãøm P quay âãöu xung quanh M våïi váûn täúc goïc ω bàòng hàòng säú :
/2
v( ) Rz
Pe
ω
=×
JJJG
GG
MP
Biãøu diãùn trong cå cåí (, , )
rz
eee
θ
G
GGcuía R2, ta coï :
Våïi : vaì :
0
0
1
z
e
⎧
⎪
=⎨
⎪
⎩
Gcos
sin
0
dt
M
Pd t
ω
ω
⎧
⎪
=⎨
⎪
⎩
JJJG ⇒ /2
sin
v( ) cos
0
R
dt
Pdt
ω
ω
ω
ω
−
⎧
⎪
=⎨
⎪
⎩
G
⇒
()
2
/2 2
/2
/2
cos
v( )
() sin
0
R
R
R
dt
dP
aP d t
dt
ω
ω
ω
ω
⎧−
⎛⎞
⎪
==−
⎨
⎜⎟
⎝⎠
⎪
⎩
G
G
(Ghi chuï :
+ Caïc vectå noïi trãn âæåüc biãøu diãøn trong cåí såí (, , )
rz
eee
θ
G
GG
+ Caïc khaïc âãø xaïc âënh : Trong R
/
v( ) R
P
G
22, ngæåìi chåi xaì treo quay
âãöu quanh quanh âiãøm M nãn coï giaï trë :
/2
v( ) R
P
G.
M
P
ω
, cuìng chiãöu
våïi chuyãøn âäüng , nàòm trong màût phàóng chuyãøn âäüng vaì
. Do âoï coï thãø viãút ngay :
/2
v( ) R
PM⊥
GPt
/2
sin
v( ) cos
0
R
dt
Pd
ω
ω
ω
ω
−
⎧
⎪
=⎨
⎪
⎩
G
C
D O A z
B
M
P
T θ
e
θ
G
z
e
G
r
e
G
T
M
P
θ
ω
t
⊗
e
θ
G
z
e
G
r
e
G
T
M
P
θ
ωt
⊗
/R2
v(P)
G
ϖ
3
Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
+ Caïch khaïc âãø xaïc âënh : Do trong R
/2
()
R
aP
G
2, ngæåìi chåi xaì treo quay âãöu quanh âiãøm M
våïi váûn täúc goïc ω nãn gia täúc trong R2 chè coï thaình pháön hæåïng tám hæåïng tæì P vãö M, giaï trë
bàòng 2
M
P
ω
, suy ra :
2
22
/2
cos
() sin
0
R
dt
aP MP d t
ω
ω
ω
ωω
⎧−
⎪
=− = −
⎨
⎪
⎩
JJJG
G)
Gia täúc Coriälêt cuía âiãøm P :
2/ 1 / 2
() 2 v()
CRR
aP P=Ω ×
G
GG
R
våïi : 2/ 2RR z
e
θ
Ω=
G
G
Biãøu diãùn trong cå såí (, , )
rz
eee
θ
G
GG : aP
/2
() 2 v()
CzR
e P
θ
=×
GGG
0
0
2 cos ( cos )
() 2 cos ( sin )
0
C
td t
aP t d t
θ
ωωω ω
θ
ωωω ω
−
⎧
⎪
=−
⎨
⎪
⎩
G⇒
22
0
2
0
2cos)
() 2 cos sin )
0
C
dt
aP d t t
θω ω
θ
ωωω
⎧−
⎪
=−
⎨
⎪
⎩
G
Gia täúc theo cuía âiãøm P :
2
()
ez
aP e OP OP
θθ
=×−
JJJG JJJG
GG
⇒
22 2
00
22
00
sin ( cos ) cos
( ) ( cos ) sin sin cos
0
e
dtbdt t
aP b d t t d t t
θω ω θ ω ω
θ
ωωωθω
⎧⎡⎤
−+
⎣⎦
⎪
⎪
ω
⎡
⎤
=−+ −
⎨
⎣
⎦
⎪
⎪
⎩
G
Taûi t
π
ω
= thç : t
ω
π
= (chán P åí trãn cao) ⇒
2
/2
2
0
22
0
()
() 2
() ( )
Rr
Cr
er
aP de
aP de
aP b de
ω
θω
θω
⎧=
⎪=
⎨
⎪=− −
⎩
G
G
GG
G
G
Gia täúc theo cuía âiãøm P trong hãû quy chiãúu traïi âáút R1 :
/1 /2
() () () ()
Re C R
aP a P a P aP=++
GGGG
⇒ 22
/1 0 0
() [ 2 ( )]
Rr
aP d d b d e
ωθθ
=+−−
G
G
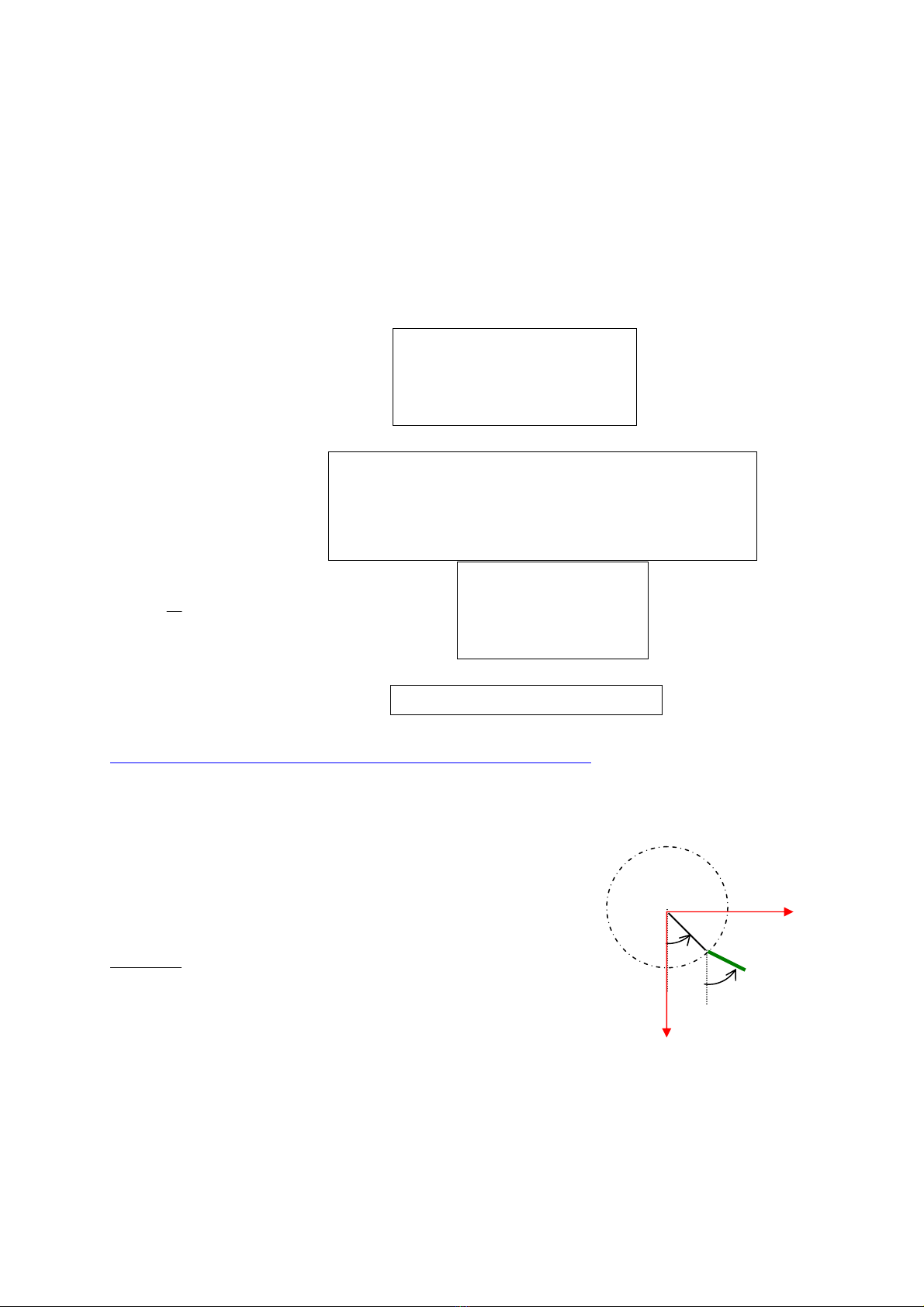
@AÏp duûng 2 (Trang 16): Momen âäüng læåüng cuía mäüt thanh:
Hai cháút âiãøm A vaì B, giäúng nhau, khäúi læåüüng m, âæåüc liãn kãút våïi nhau bàòng mäüt thanh chiãöu
daìi b, khäúi læåüng khäng âaïng kãø.
A chuyãøn âäüng trãn mäüt voìng troìn tám O, baïn kênh b, vaì thanh AB coï thãø dao âäüng xung
quanh mäüt truûc âi qua A vaì vuäng goïc våïi màût phàóng chuyãøn
âäüng.
O
A
B
β
α
x
y
Tênh âäüng læåüng vaì momen âäüng læåüng cuía hãû AB âäúi våïi âiãøm
O theo caïc goïc α , β vaì caïc âaûo haìm cuía chuïng.
Baìi giaíi :
Phæång phaïp 1 : (Duìng âënh nghéa) :
GG
Ta coï : ⇒
i
.v
i
i
Pm=∑GGG
i
v( ) v( )PmA mB=+
i
v
Oi
i
L
OM m=×
∑JJJJJG
GG ⇒ v( ) v( )
O
LOAmAOBmB=× +×
J
JJG JJJG
G
G
G
Våïi :
cos
sin
0
b
OA b
α
α
⎧
⎪
=⎨
⎪
⎩
JJJG
sin
v( ) cos
0
b
Ab
α
α
α
α
−
⎧
⎪
=⎨
⎪
⎩
G
4
Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
(cos cos )
(sin sin )
0
b
OB b
α
β
α
β
+
⎧
⎪
=+
⎨
⎪
⎩
JJJG
(sin sin)
v( ) ( cos cos )
0
b
Bb
α
αβ
β
α
αβ β
⎧−+
⎪
=+
⎨
⎪
⎩
G
Suy ra :
(2 sin sin )
(2 cos cos )
0
mb
Pmb
α
αβ
β
α
αβ β
⎧−+
⎪
=+
⎨
⎪
⎩
G
22()cos()
Oz
L
mb e
αα α
ββ β
⎡
⎤
=+++−
⎣
⎦
G
G
Phæång phaïp 2 : Duìng âënh lyï Koenig :
Ta coï :
()
v( ) 2 v( )
i
PmGm==
∑
GGG
G
Våïi :
1
(cos cos )
2
1
(sin sin )
2
0
b
OG ⇒
1
(sin sin)
2
1
v( ) ( cos cos )
2
0
b
Gb
α
αβ
β
α
αββ
⎧−+
⎪
⎪
⎪
=+
⎨
⎪
⎪
⎪
⎩
G
b
α
β
α
β
⎧+
⎪
⎪
⎪
=+
⎨
⎪
⎪
⎪
⎩
JJJG
Suy ra :
(2 sin sin )
(2 cos cos )
0
mb
Pmb
α
αβ
β
α
αβ β
⎧−+
⎪
=+
⎨
⎪
⎩
G
Âënh lyï Koenig vãö momen âäüng læåüng : *
v( )
OG
LOGmGL
=
×+
J
JJG
G
G
G
Trong âoï : . Maì :
*v( )* v(B)*
G
LGAmA GBm=× +×
JJJG JJJG
GGG
GA GB=−
J
JJG JJJG. Màûc khaïc, trong hãû quy chiãúu
khäúi tám R*, thanh AB quay quanh G nãn váûn täúc v( )* v(B)*A
=
−
G
G, v(B)* GB⊥
G
Suy ra : *2v(
G
LGBmB=× )*
J
JJG
GG
1cos
2
1sin
2
0
b
GB b
β
β
⎧
⎪
⎪
⎪
=⎨
⎪
⎪
⎪
⎩
JJJG
1sin
2
1
v( )* cos
2
0
b
Bb
β
β
β
β
⎧−
⎪
⎪
⎪
=⎨
⎪
⎪
⎪
⎩
G
Suy ra : v( ) 2 v( )*
O
LOGmG GBmB=× + ×
JJJG JJJG
G
G
G⇒ 22()cos()
Oz
L
mb e
αα α
ββ β
⎡
⎤
=+++−
⎣
⎦
G
G
(Læu yï cáön tênh vaì )
OG
JJJG
v( )G
G
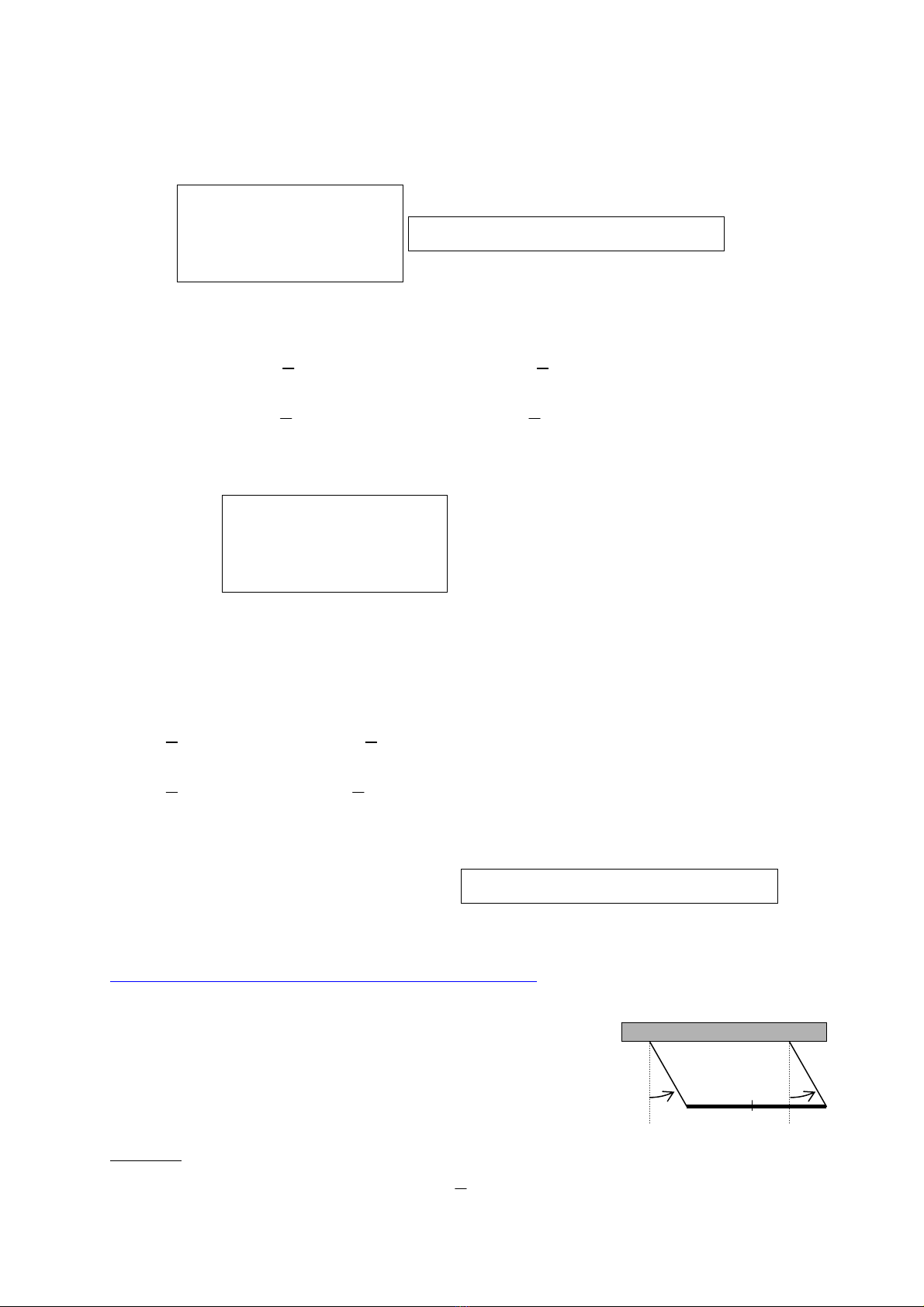
@ AÏp duûng 3 (Trang 20):Thanh treo trãn hai såüi dáy
Thanh AB âäöng cháút, tám G, khäúi læåüng m, âæåüc treo trãn hai såüi
dáy AA’ vaì BB’ giäúng nhau, chiãöu daìi b. Thanh dao âäüng trong
màût phàóng thàóng âæïng, caïc dáy AA’ vaì BB’ luän luän song song
våïi nhau. G
B
A
α
α
A’ B’
Tênh âäüng nàng cuía thanh theo âaûo haìm
α
cuía goïc nghiãng
α
cuía caïc såüi dáy taûi thåìi âiãøm t cho træåïc.
Baìi giaíi :
AÏp duûng âënh lyï Koenig vãö âäüng nàng : 2*
1v( )
2
K
K
E
mGE=+
5
