
Algo2010N15-NguyenThiThanhVi-NgoVanVi-NhamNgocTrung-CNPMK52
TR NG Đ I H C BÁCH KHOA HÀ N IƯỜ Ạ Ọ Ộ
VI N CÔNG NGH THÔNG TIN VÀ TRUY N THÔNGỆ Ệ Ề
BÀI T P L NẬ Ớ
THI T K VÀ PHÂN TÍCH THU T TOÁNẾ Ế Ậ
Đ TÀIỀ 15: BÀI TOÁN TÔ M U Đ THẦ Ồ Ị
Giáo viên h ng d n: PGS. NGUY N Đ C NGHĨAướ ẫ Ễ Ứ
Sinh viên th c hi n : ự ệ
1. Nguy n Th Thanh Viễ ị 20073430 CNPM K52
2. Ngô Văn Vĩ 20073500 CNPM K52
3. Nhâm Ng c Trungọ20073050 CNPM K52
Hà N i, 12/2010ộ
1 | P a g e

Algo2010N15-NguyenThiThanhVi-NgoVanVi-NhamNgocTrung-CNPMK52
M C L CỤ Ụ
M C L CỤ Ụ ......................................................................................................................................... 2
2.4. ng d ngỨ ụ ........................................................................................................................... 7
2.1. Đ c d li u t fileọ ữ ệ ừ ............................................................................................................ 36
2.2. D li u vào t bàn phímữ ệ ừ .................................................................................................. 49
PH L C 1: DANH M C CÁC HÌNH NH TRONG TÀI LI UỤ Ụ Ụ Ả Ệ ....................................................... 64
I. GI I THI U BÀI TOÁNỚ Ệ
1. T ng quan v đ thổ ề ồ ị
1.1. Đ th và các cách bi u di n đ th ồ ị ể ễ ồ ị
Đ th là gìồ ị
M t cách không chính th c, đ th là m t t p các đ i t ng đ c g i là các đ nh (ho c nút)ộ ứ ồ ị ộ ậ ố ượ ượ ọ ỉ ặ
n i v i nhau b i các c nhố ớ ở ạ (ho c cung). C nh có th có h ng ho c vô h ng. Đ th th ngặ ạ ể ướ ặ ướ ồ ị ườ
đ c v d i d ng m t t p các đi m (các đ nh n i v i nhau b ng các đo n th ng (các c nh).ượ ẽ ướ ạ ộ ậ ể ỉ ố ớ ằ ạ ẳ ạ
Đ th bi u di n đ c r t nhi u c u trúc, nhi u bài toán th c t có th đ c bi u di n b ngồ ị ể ễ ượ ấ ề ấ ề ự ế ể ượ ể ễ ằ
đ th . Ví d , c u trúc liên k t c a m t website có th đ c bi u di n b ng m t đ th cóồ ị ụ ấ ế ủ ộ ể ượ ể ễ ằ ộ ồ ị
h ng nh sau: các đ nh là các trang web hi n có t i website, t n t i m t c nh có h ng n iướ ư ỉ ệ ạ ồ ạ ộ ạ ướ ố
t trangừ A t i trangớ B khi và ch khiỉ A có ch a 1 liên k t t iứ ế ớ B.
C u trúc đ th có th đ c m r ng b ng cách gán tr ng s cho m i c nh. Có th s d ngấ ồ ị ể ượ ở ộ ằ ọ ố ỗ ạ ể ử ụ
đ th có tr ng s đ bi u di n nhi u khái ni m khác nhau. Ví d , n u đ th bi u di n m tồ ị ọ ố ể ể ễ ề ệ ụ ế ồ ị ể ễ ộ
m ng đ ng giao thông, các tr ng s có th là đ dài c a m i con đ ng. M t cách khác đạ ườ ọ ố ể ộ ủ ỗ ườ ộ ể
m r ng đ th c b n là qui đ nh h ng cho các c nh c a đ th (nh đ i v i các trangở ộ ồ ị ơ ả ị ướ ạ ủ ồ ị ư ố ớ
web, A liên k t t iế ớ B, nh ngư B không nh t thi t cũng liên k t t iấ ế ế ớ A). Lo i đ th này đ c g iạ ồ ị ượ ọ
là đ th có h ng. M t đ th có h ng v i các c nh có tr ng s đ c g i là m t l i.ồ ị ướ ộ ồ ị ướ ớ ạ ọ ố ượ ọ ộ ướ
2 | P a g e
Algo2010N15-NguyenThiThanhVi-NgoVanVi-NhamNgocTrung-CNPMK52
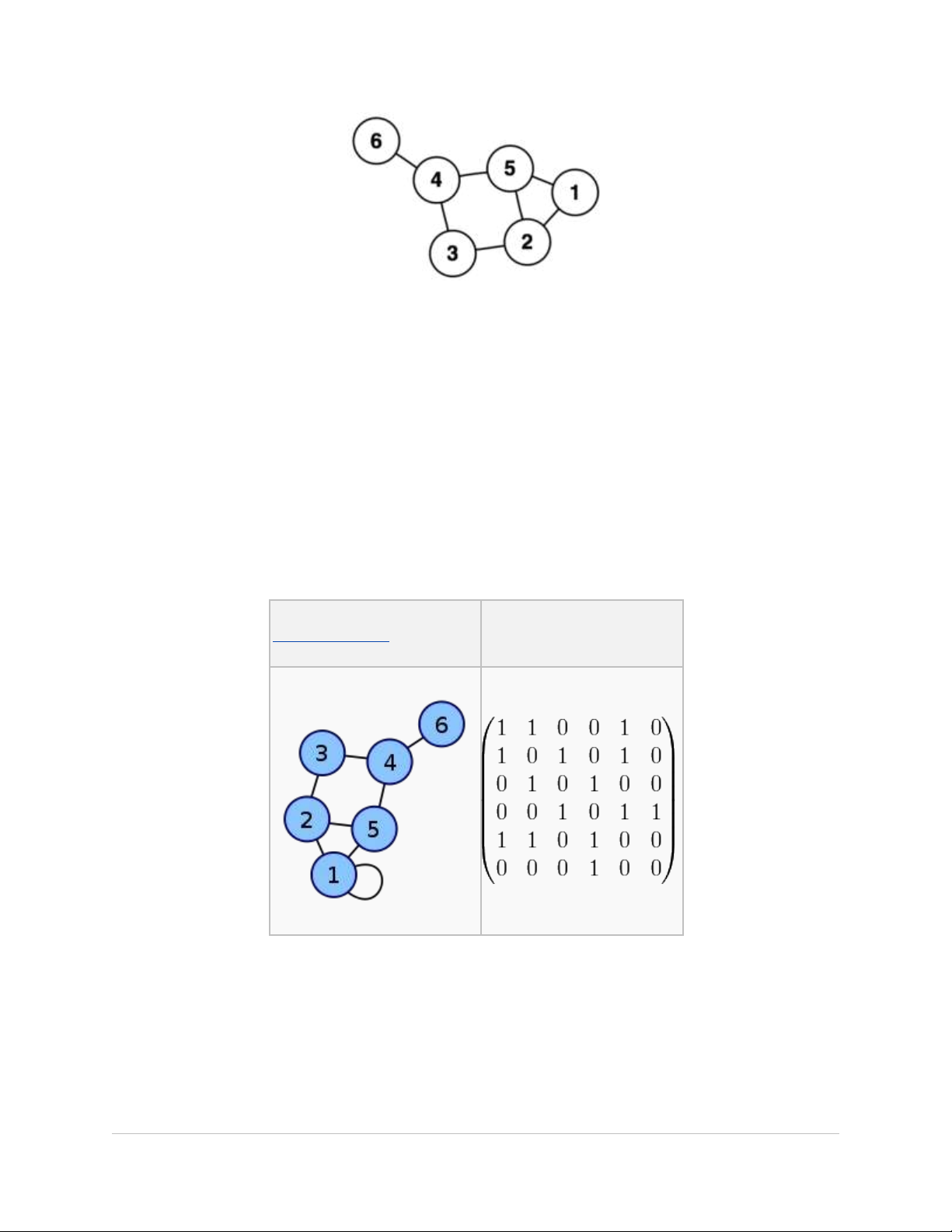
Hình 01: Đ th vô h ngồ ị ướ
Các cách bi u di n đ thể ễ ồ ị
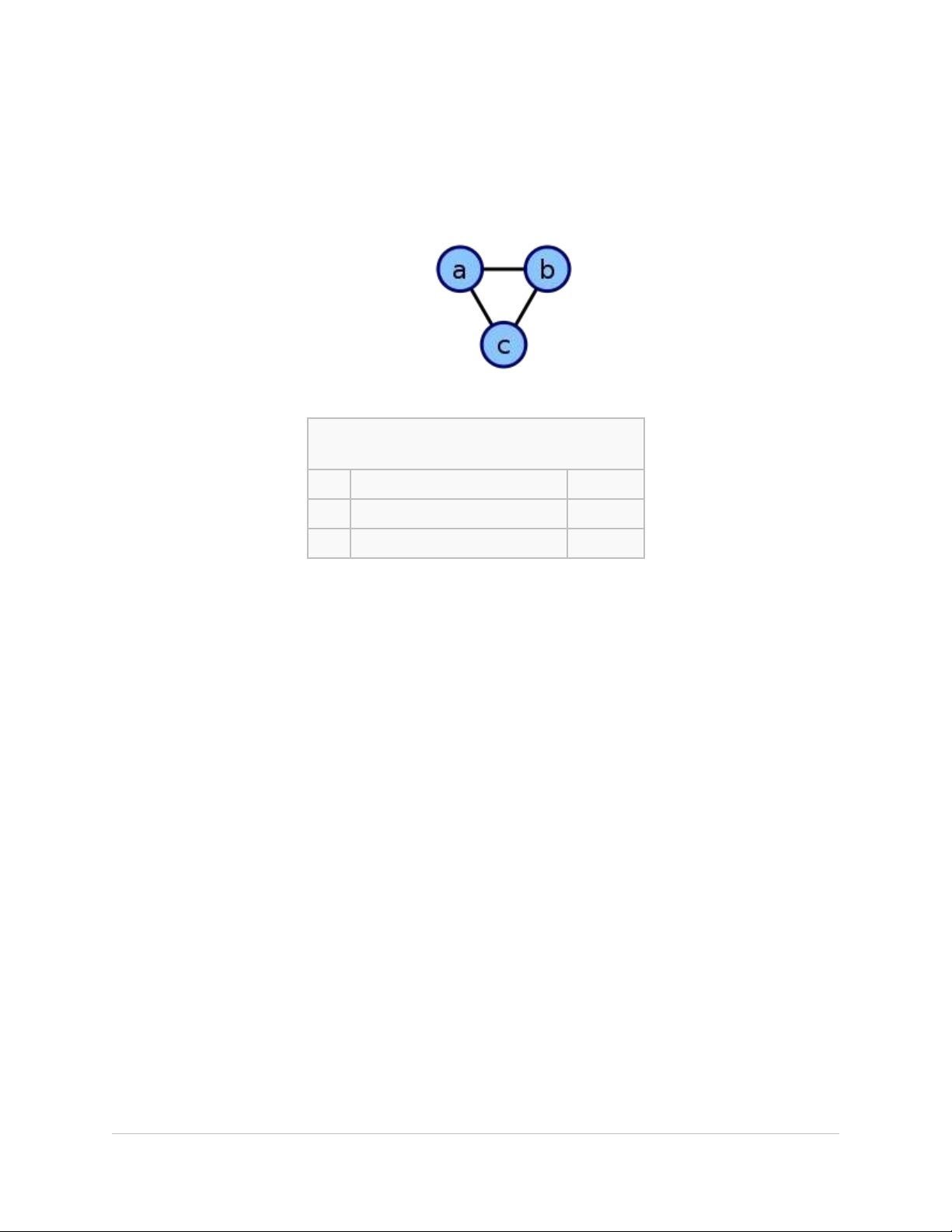
-Ma tr n kậ ề (Adjaceny matrix) - m t ma tr nộ ậ N × N, trong đó N là s đ nh c a đ th .ố ỉ ủ ồ ị
N u có m t c nh nào đó n i đ nhế ộ ạ ố ỉ viv i đ nhớ ỉ vj thì ph n tầ ử Mi,j b ng 1, n u không, nóằ ế
có giá tr 0. C u trúc này t o thu n l i cho vi c tìm các đ th con và đ đ o các đị ấ ạ ậ ợ ệ ồ ị ể ả ồ
th .ị
Labeled graph Adjacency matrix
-Danh sách kề (Adjacency list) - M i đ nh c a đ th có m t danh sách các đ nh k nóỗ ỉ ủ ồ ị ộ ỉ ề
(nghĩa là có m t c nh n i t đ nh này đ n m i đ nh đó). Trong đ th vô h ng, c uộ ạ ố ừ ỉ ế ỗ ỉ ồ ị ướ ấ
trúc này có th gây trùng l p. Ch ng h n n u đ nh 3 n m trong danh sách c a đ nh 2ể ặ ẳ ạ ế ỉ ằ ủ ỉ
thì đ nh 2 cũng ph i có trong danh sách c a đ nh 3. L p trình viên có th ch n cách sỉ ả ủ ỉ ậ ể ọ ử
3 | P a g e
Algo2010N15-NguyenThiThanhVi-NgoVanVi-NhamNgocTrung-CNPMK52
d ng ph n không gian th a, ho c có th li t kê các quan h k c nh ch m t l n.ụ ầ ừ ặ ể ệ ệ ề ạ ỉ ộ ầ
Bi u di n d li u này thu n l i cho vi c t m t đ nh duy nh t tìm m i đ nh đ c n iể ễ ữ ệ ậ ợ ệ ừ ộ ỉ ấ ọ ỉ ượ ố
v i nó, do các đ nh này đã đ c li t kê t ng minh.ớ ỉ ượ ệ ườ
The graph pictured above has this
adjacency list representation:
a adjacent to b,c
b adjacent to a,c
c adjacent to a,b
1.2. Các bài toán đi n hìnhể
-Bài toán t p con đ c l pậ ộ ậ
-Bài toán tô m u đ thầ ồ ị
-Bài toán tìm đ ng đi ng n nh tườ ắ ấ
-Bài toán lu ng c c đ iồ ự ạ
-Bài toán ph t i thi uủ ố ể
-Ki m tra tính liên thông c a đ thể ủ ồ ị
-Duy t đ thệ ồ ị
-…
2. Bài toán tô m u đ thầ ồ ị
Tô màu đ th và s t ng quát c a nó là công c h u d ng trong vi c mô hình hóa r t nhi uồ ị ự ổ ủ ụ ữ ụ ệ ấ ề
bài toán khác nhau trong v n đ x p l ch, xây d ng ch ng trình và v n đ phân công côngấ ề ế ị ự ươ ấ ề
4 | P a g e
Algo2010N15-NguyenThiThanhVi-NgoVanVi-NhamNgocTrung-CNPMK52
vi c. Bài toán tô màu đ th bao g m nhi u lo i: tô màu đ nh đ th (vertex graph coloring) , tôệ ồ ị ồ ề ạ ỉ ồ ị
màu c nh đ th (edge graph coloring) ...ạ ồ ị
2.1. Bài toán tô m u c nhầ ạ
Bài toán
Cho G=(V,E) là đ n đ th vô h ng ( G không là đ th khuyên) , hãy tìm cách gán (tô màu)ơ ồ ị ướ ồ ị
cho m i c nh c a đ th m t màu sao cho hai c nh có cùng chung 1 đ nh không b tô b i cùngỗ ạ ủ ồ ị ộ ạ ỉ ị ở
m t màu. M t phép gán màu cho các c nh nh v y g i là m t phép tô màu c nh đ th . Nóiộ ộ ạ ư ậ ọ ộ ạ ồ ị
cách khác, phép tô c nh đ th b i k màu nói trên có th đ c hi u là m t phân ho ch c a t pạ ồ ị ở ể ượ ể ộ ạ ủ ậ
c nh E c a G thành k t p con (t ng ng v i k màu) sao cho m i t p con ng v i m t màu iạ ủ ậ ươ ứ ớ ỗ ậ ứ ớ ộ
nh t đ nh. Bài toán đ t ra là tìm cách tô màu nào s d ng s màu ít nh t có th .ấ ị ặ ử ụ ố ấ ể
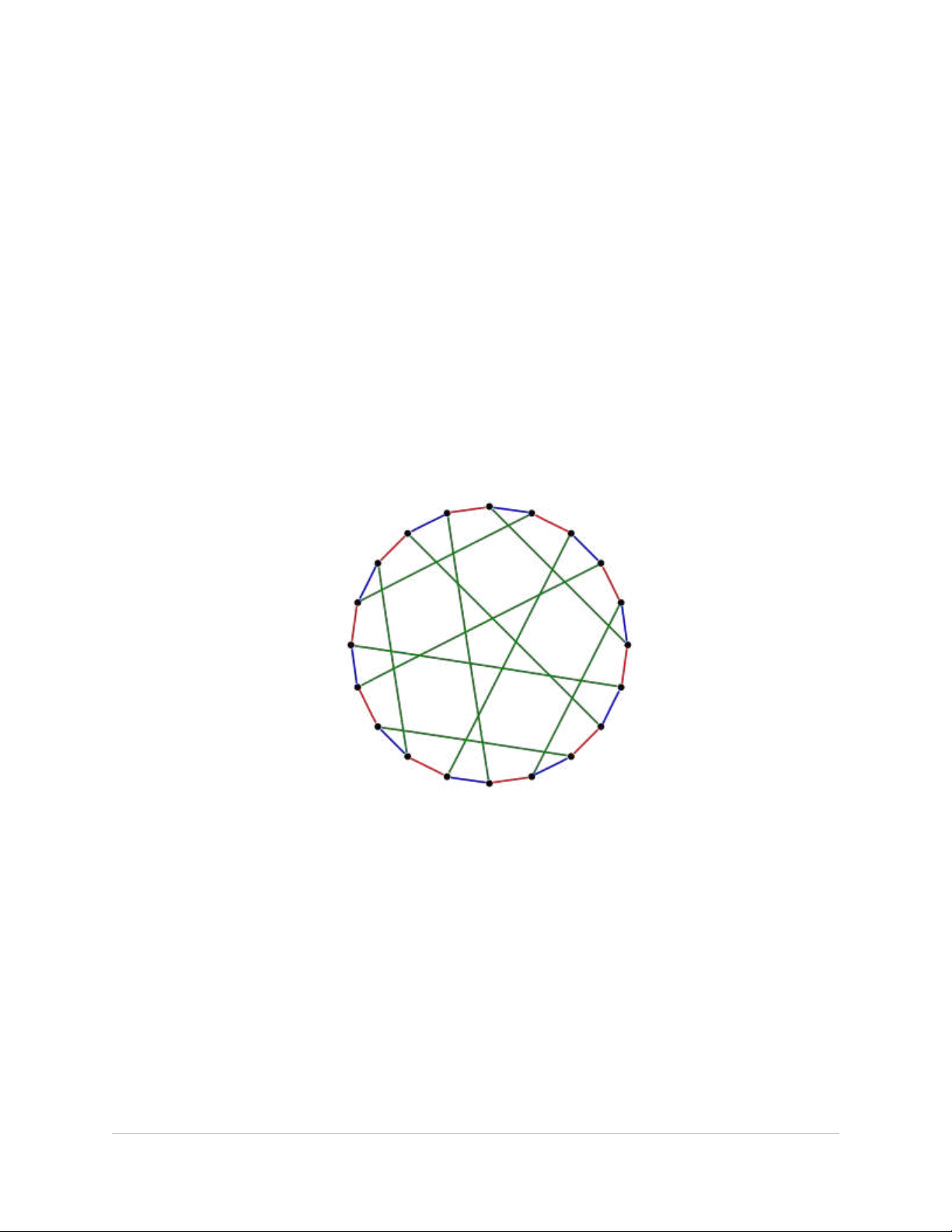
Ví dụ
Đ th trong hình trên có th tô b i 4 màu. Đ th G g i là tô đ c b i k màu-c nh n u G cóồ ị ể ở ồ ị ọ ượ ở ạ ế
m t phép tô k màu-c nh phù h p.Thông th ng h u h t các đ th không là đ th khuyên đ uộ ạ ợ ườ ầ ế ồ ị ồ ị ề
tô đ c.Và n u G có tính ch t nh v y thì G cũng có th tô b i l màu v i l>k.ượ ế ấ ư ậ ể ở ớ
2.2. Bài toán tô m u đ nhầ ỉ
M t phép tô m u s d ng nhi u nh t k m u g i là m t phép tô k m u. S l ng m u nhộ ầ ử ụ ề ấ ầ ọ ộ ầ ố ượ ầ ỏ
nh t c n đ tô các đ nh c a đ th G g i là s c s đ nh c a đ th G, sao cho không có haiấ ầ ể ỉ ủ ồ ị ọ ắ ố ỉ ủ ồ ị
đ nh k nhau nào đ c tô cùng m u. ỉ ề ượ ầ
5 | P a g e












![Bài tập lớn: Xây dựng class quản lý quán coffee [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250612/minhquan0690/135x160/59971768205789.jpg)













