Ch ngươ 1
Bài 1-1
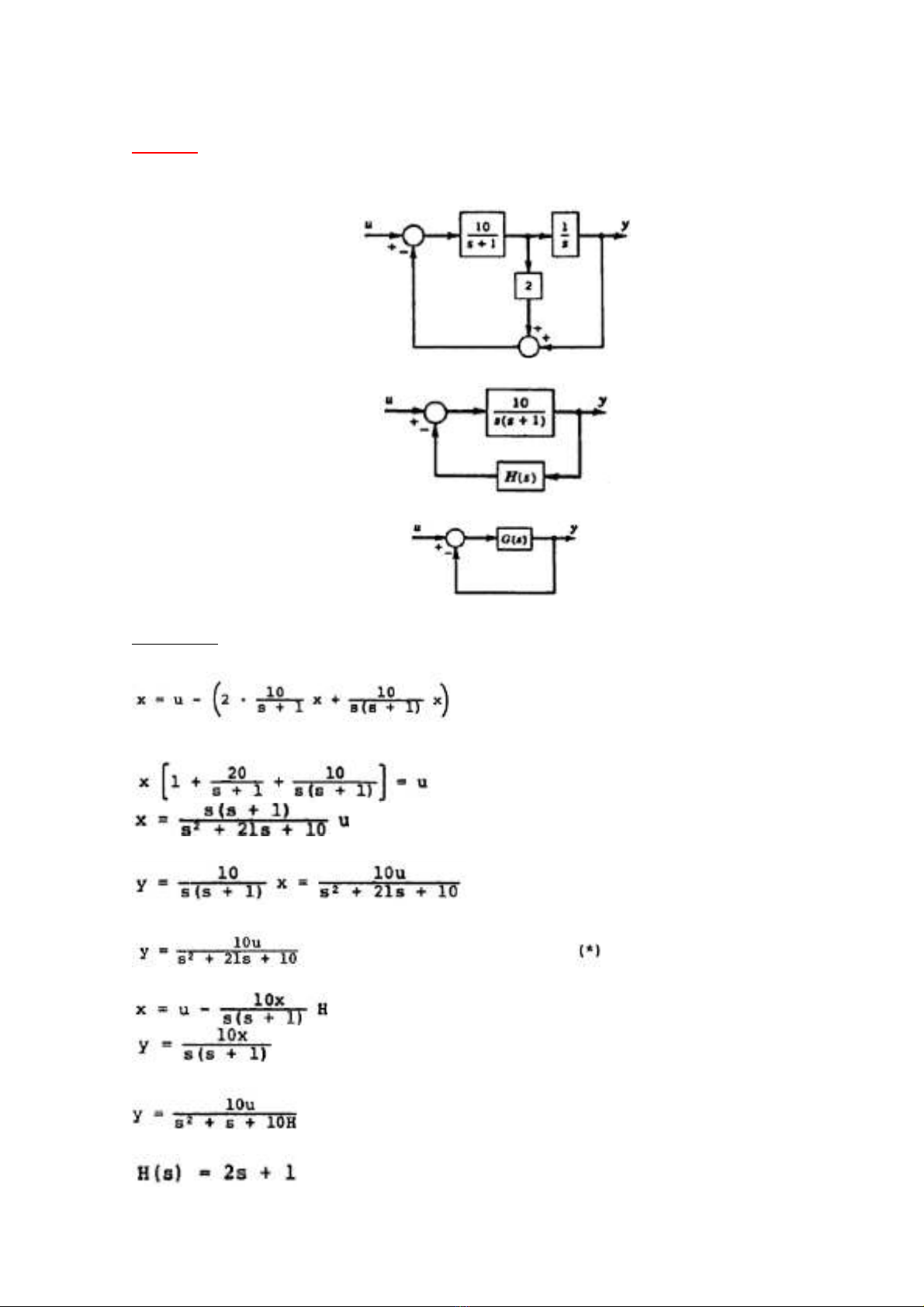
Cho sơ đồ kh iố c aủ hệ th ngố như hình 1. Sơ đồ kh iố c aủ hệ th ngố đ cượ
chuy nể đ iổ như hình 2 và hình 3
Hình 1
Hình 2
Hình 3
L iờ gi i:ả
Th cự hi nệ c ngộ t iạ đi mể x c aủ hình 1, tai đây ta có:
Hay
Từ sơ đồ kh iố và ph ngươ trình trên ta có:
V iớ sơ đồ hệ th ngố ở hình 2 và 3 chúng ta ph iả tìm m iố quan hệ gi aữ y và u
Hình 2 ta c ngộ t iạ đi mể x:
K tế h pợ 2 ph ngươ trình ta có:
So sánh v iớ (*) ta có:
Trong hình 3:
CuuDuongThanCong.com https://fb.com/tailieudientucntt
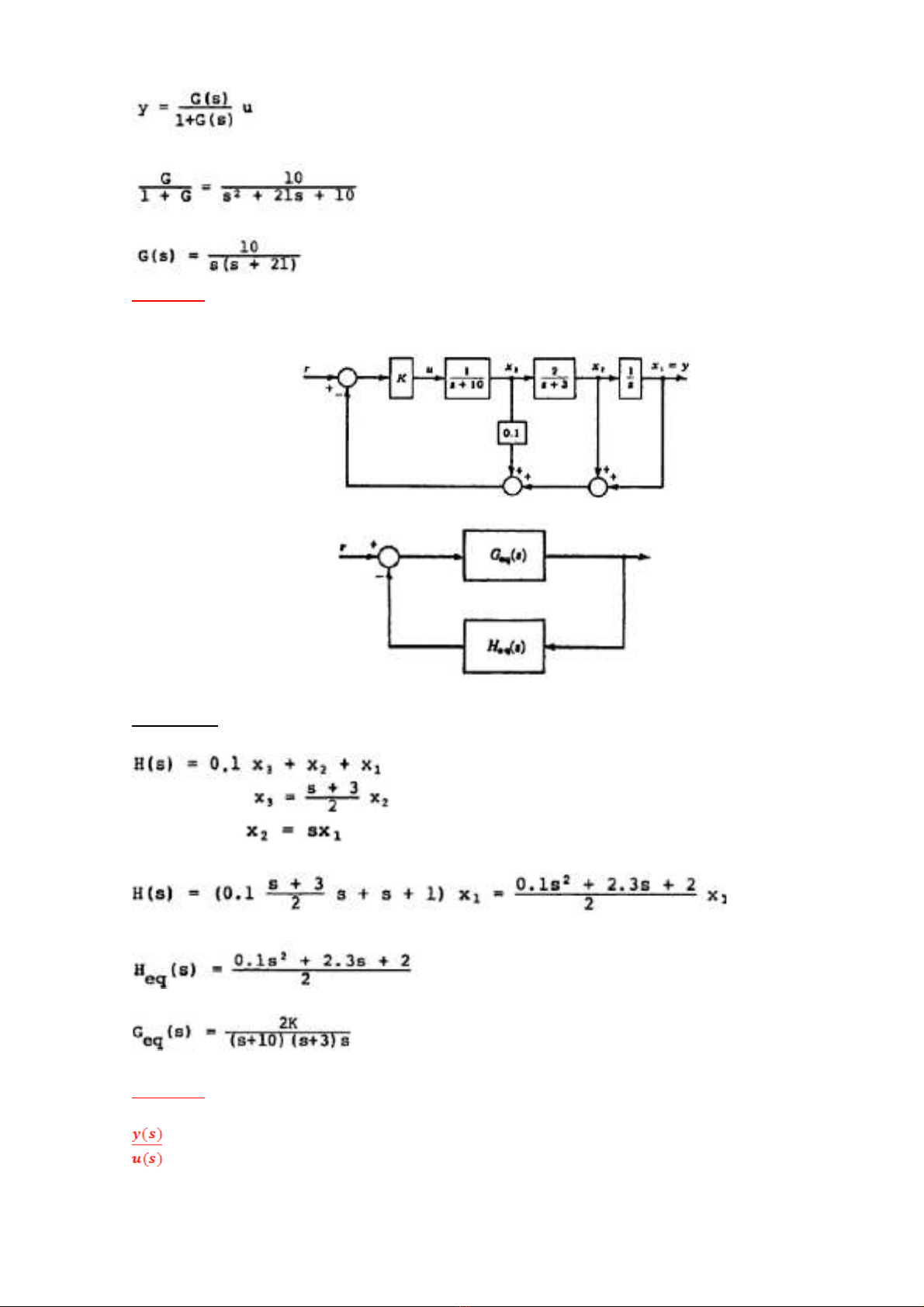
Đ ngồ nh tấ v iớ ph ngươ trình (*):
V y:ậ
Bài 1-2:
Cho hệ th ngố đi uề khi nể vòng kín như hình 1. Tìm Geq(s) và Heq(s) c aủ hệ
th ngố cho b iở hình 2.
Hình 1
Hình 2
L iờ gi i:ả
Từ sơ đồ kh iố ở hình 1 ta có đ cượ khâu ph nả h iồ c aủ hệ th ng:ố
Và
Thay vào khâu ph nả h i:ồ
V iớ y = x1, ta có đ cượ hàm truy nề c aủ khâu ph nả h i:ồ
Từ sơ đồ kh iố hình 1 ta có:
Bài 1-5:
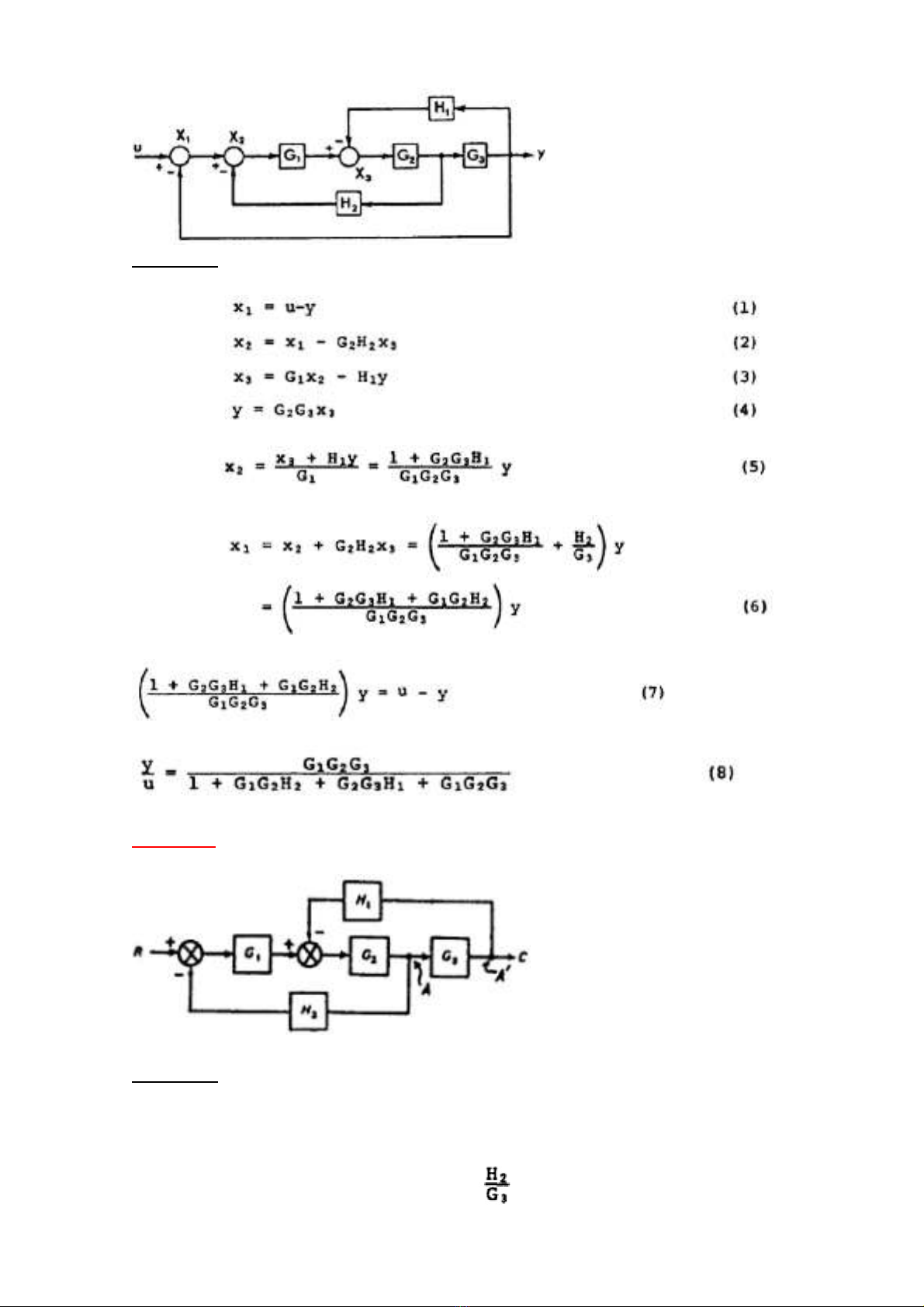
Cho hệ th ngố đ cượ trình bày hình d i.ướ Hãy tìm m iố quan hệ gi aữ u và y (
) là 1 hàm theo H1, H2, G1, G2 và G3.
CuuDuongThanCong.com https://fb.com/tailieudientucntt
L iờ gi i:ả
Từ sơ đồ kh iố trên ta có đ cượ ph ngươ trình:
Từ ph ngươ trình (3) và (4) thay vào x2:
L yấ ph ngươ trình (5) thế vào ph ngươ trình (2):
Thế ph ngươ trình (6) vào ph ngươ trình (1):
Như v y:ậ
Bài 1- 6:
Cho sơ đồ kh iố c aủ hệ th ngố như sau:
Hãy tìm hàm truy nề c aủ hệ th ngố và t iố gi nả sơ đồ kh iố.
L iờ gi i:ả
Hệ th ngố có 2 khâu ph nả h i.ồ Ta s pắ x pế l iạ sao cho chỉ còn 1 khâu ph nả h i.ồ
Chuy nể đi mể A c aủ khâu ph nả h iồ phía d iướ t iớ đi mể A’ thì ph iả bi nế đ iổ H2
thành
CuuDuongThanCong.com https://fb.com/tailieudientucntt
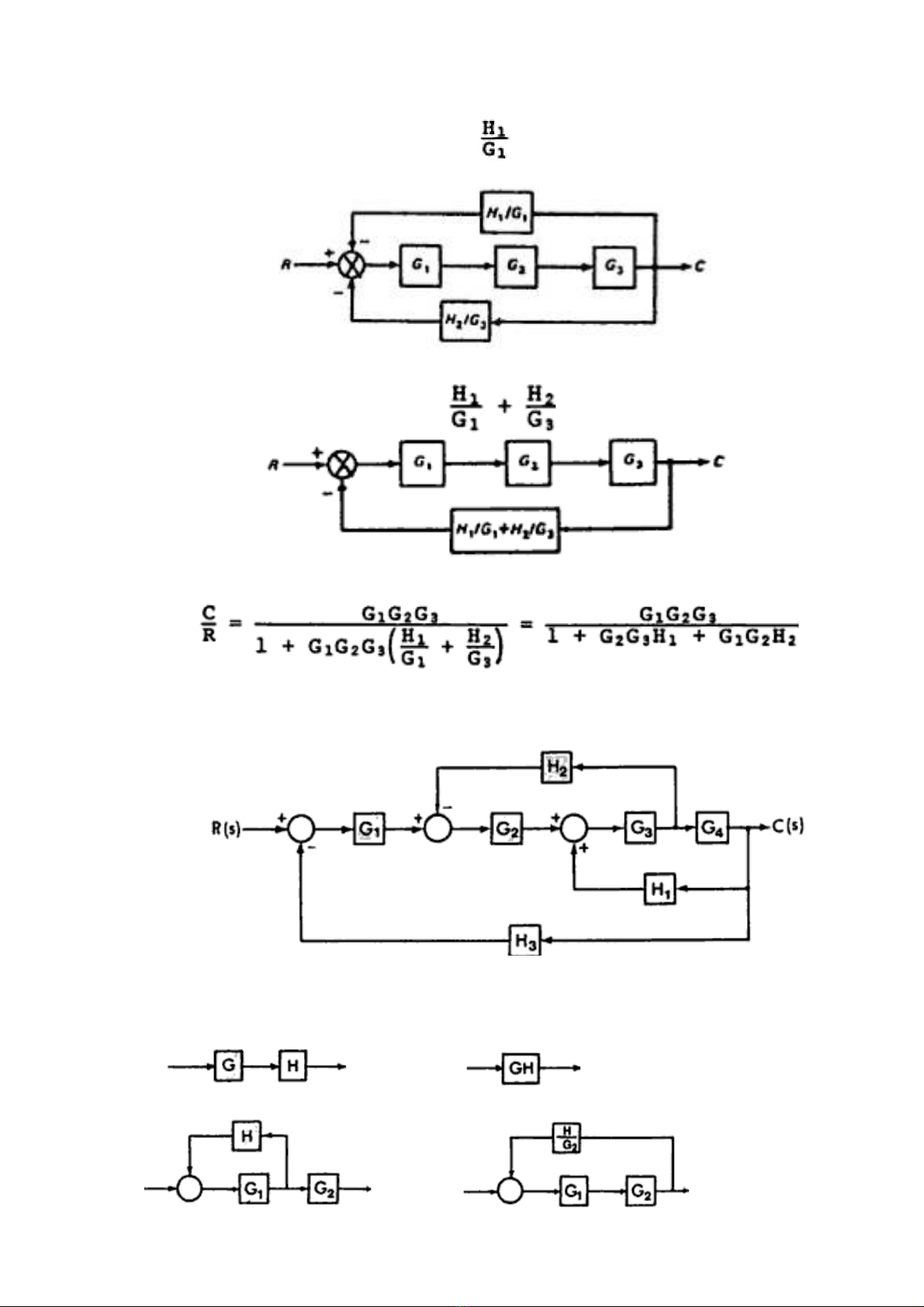
Chuy nể đi mể B ở phía trên t iớ đi mể B’ thì H1 đ cượ bi nế đ iổ thành:
Sơ đồ kh iố đ cượ chuy nể đ iổ t ngươ đ ngươ thành:
2 khâu ph nả h iồ đ cượ chuy nể thành 1 khâu , v iớ :
Từ sơ đồ kh iố v aừ có, ta có đ cượ hàm truy nề đ cượ đ nơ gi nả hóa như sau:
Bài 1-7: Thu g nọ sơ đồ c aủ hệ th ngố đi uề khi nể vòng kín nhi uề vòng hình
d iướ thành sơ đồ đ nơ gi n:ả
Gi i:ả
Để có thể thu g nọ sơ đồ trên c nầ ph iả dùng nh ngữ quy t cắ sau:
+ thành
+ thành
CuuDuongThanCong.com https://fb.com/tailieudientucntt
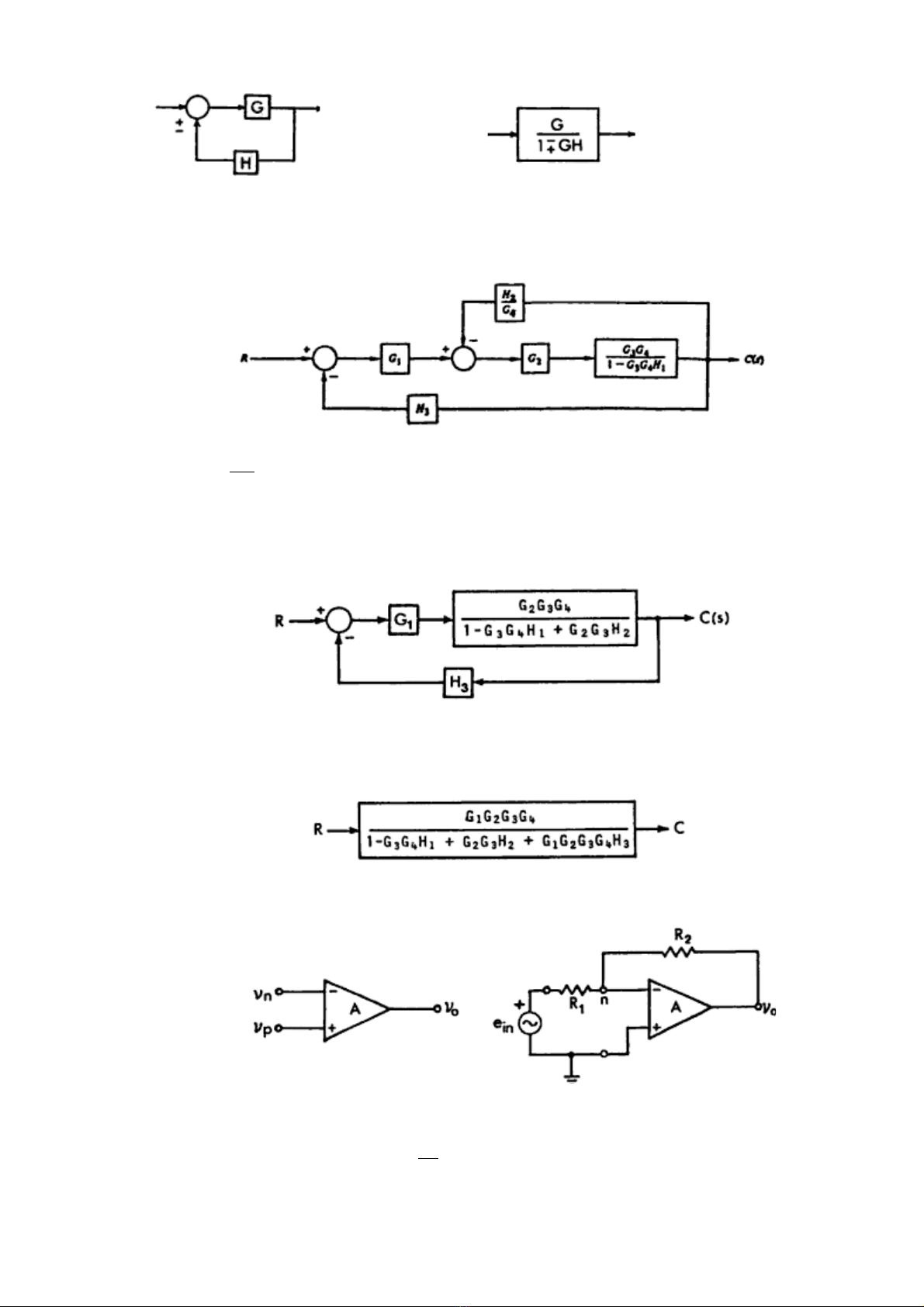
+ thành
Sử d ngụ quy t cắ 2 sẽ chuy nể đ cượ kh iố H2 ra sau kh iố G4. Sử d ngụ quy t cắ 3
sẽ khử đ cượ vòng G3.G4. G1. Đ aư ra đ cượ sơ đồ t ngươ đ ngươ như hình d i.ướ
Khử vòng
2
4
H
G
sẽ đ c:ượ
Cu iố cùng, thu g nọ l iạ theo nguyên t cắ 1 khử vòng H3 đ cượ sơ đồ thu g nọ như
hình d i:ướ
Bài 1- 8: Mô hình m chạ khu chế đ iạ đ cượ đ aư ra như hình d i:ướ
-Cho
4
10A>
-Tính hệ số khu chế đ iạ
0
in
V
e
CuuDuongThanCong.com https://fb.com/tailieudientucntt