
BÀI T P SINH H CẬ Ọ
LAI M T C P TÍNH TR NG:Ộ Ặ Ạ
D ng thu nạ ậ
Bài 1: Cho giao ph n gi a cây thu n ch ng có thân cao ấ ữ ầ ủ
v i cây thu n ch ng thân th p thu đc Fớ ầ ủ ấ ượ 1 đu có thân ề
cao. Cho F1 lai v i nhau thu đc Fớ ượ 2.
a) Có nh n xét gì v đc đi m di truy n tính tr ng ậ ề ặ ể ề ạ
chi u cao thân cây. L p s đ lai t P ề ậ ơ ồ ừ
F2.
b) N u cho F ế1 lai phân tích thì k t qu con lai nh th ế ả ư ế
nào?
Gi iả
a) Di truy n theo hi n t ng tr i hoàn toànề ệ ượ ộ
* Quy c gen: A là thân cao, a là thân th pướ ấ
* Xác đnh ki u gen c a b m (P):ị ể ủ ố ẹ
-Thân cao thu n ch ng: AAầ ủ
-Thân th p thu n ch ng: aaấ ầ ủ
* S đ lai:ơ ồ
P: AA( Thân cao) x aa (Thân cao)
GP: A a
F1: Aa (100 % thân cao)
F1 x F1: Aa (thân cao) x Aa (thân cao)
GF1: A, a A, a
F2: AA , Aa , Aa , aa
- T l ki u gen: 1AA : 2Aa : 1aaỉ ệ ể
- T l ki u hình: 3 cao : 1 th pỉ ệ ể ấ
b) F1 lai phân tích: Aa (thân cao) x aa (thân th p)ấ
GF1: A,a a
FB: Aa aa
- T l ki u gen: 1 Aa : 1 aaỉ ệ ể
- T l kiêu hình: 1 cao : 1 th pỉ ệ ấ
Bài 2 : Cho cà chua qu đ thu n ch ng lai v i qu vàng ả ỏ ầ ủ ớ ả
thu đc Fượ 1 đu có qu đ. Cho Fề ả ỏ 1 lai v i nhau thu đc ớ ượ
F2 .
a) Vi t s đ lai t P ế ơ ồ ừ
F2.
b) N u cho Fế1 lai phân tích thì k t qu con lai nh ế ả ư
th nào?ế
Gi iả
a)* Xác đnh ki u gen c a b m (P):ị ể ủ ố ẹ
- Qu đ thu n ch ng: AA , Qu vàng : aaả ỏ ầ ủ ả
* S đ lai:ơ ồ
P: AA (Qu đ) x aa (Qu vàng)ả ỏ ả
Gp: A a
F1: Aa(100% qu đ)ả ỏ
F1 x F1: Aa (Qu đ) x Aa ( Qu đ) ả ỏ ả ỏ
GF1: A, a A,a
F2: AA , Aa , Aa , aa
- T l ki u gen: 1AA : 2Aa : 1aaỉ ệ ể
- T l ki u hình: 3 đ : 1 vàng ỉ ệ ể ỏ
b) F1 lai phân tích: Aa (Qu đ) x aa (Qu vàng) ả ỏ ả
GF1: A, a a
FB: Aa aa
- T l ki u gen: 1 Aa : 1 aaỉ ệ ể
- T l kiêu hình: 1 đ : 1 vàngỉ ệ ỏ
Bài 3; đu Hà Lan, h t vàng tr i hoàn toàn so v i h tỞ ậ ạ ộ ớ ạ
xanh.
Cho lai gi a cây h t vàng không thu n ch ng v i nhauữ ạ ầ ủ ớ
thì k t qu F1 nh th nào?ế ả ư ế
Gi i:ả
* Quy c gen: A: h t vàng, a:h t xanhướ ạ ạ
* Xác đnh ki u gen c a b m (P):ị ể ủ ố ẹ
- H t vàng không thu n ch ng: Aaạ ầ ủ
* S đ lai:ơ ồ
P: Aa (h t vàng) x Aa (h t vàng)ạ ạ
Gp A,a A, a
F2: AA , Aa , Aa , aa
- T l ki u gen: 1AA : 2Aa : 1aaỉ ệ ể
- T l kiêu hình: 3 vàng : 1 xanh ỉ ệ
D ng ngh ch:ạ ị
Bài 4:T 1 phép lai gi a 2 cây ng i ta thu đc 92 cây ừ ữ ườ ượ
qu ng t và 31 cây qu chua.ả ọ ả
Hãy bi n lu n đ xác đnh KG, KH c a b m .ệ ậ ể ị ủ ố ẹ
Gi iả
-Xét t l ki u hình đi conỉ ệ ể ở ờ
F1( 92 qu ng t : 31 qu chua)ả ọ ả
F1( 3 qu ng t : 1 qu chua)ả ọ ả
Tuân theo đnh lu t phân li ị ậ P: Aa x Aa
* Quy c gen: A: qu ng t, a: qu chuaướ ả ọ ả
* S đ lai:ơ ồ
P: Aa (qu ng t) x Aa (qu ng t)ả ọ ả ọ
Gp: A,a A,a
F1: AA, Aa,Aa,â
- T l ki u gen: 1AA : 2Aa : 1aaỉ ệ ể
- T l kiêu hình: 3 qu ng t : 1qu chuaỉ ệ ả ọ ả
Bài 5: đu Hà Lan, gen A quy đnh thân cao, gen a quy Ở ậ ị
đnh thân th p. Cho lai cây thân cao v i cây thân th p F1ị ấ ớ ấ
thu đc 51 thân cao: 49 thân th p. ượ ấ
Hãy biên lu n và vi t s đ lai.ậ ế ơ ồ
Gi i:ả
-Xét t l ki u hình đi con:ỉ ệ ể ở ờ
F1( 51 thân cao :49 thân th p)ấ
F1( 1thân cao : 1 thân th p)ấ
đây là k t qu c a phép lai phân tích ế ả ủ P: Aa x aa
* Quy c gen: A; thân cao , a : thân th pướ ấ
* S đ lai:ơ ồ
P: Aa (thân cao) x aa ( thân th p)ấ
Gp: A, a a
F1: Aa , aa
- T l ki u gen: 1 Aa : 1 aaỉ ệ ể
- T l kiêu hình: 1 thân cao : 1 thân th pỉ ệ ấ
LAI HAI C P TÍNH TR NG:Ặ Ạ
Đ Ng c Hoàng Hânỗ ọ 1
D ng thu n:ạ ậ
* Quy c gen: A: quy đnh h t vàng, ướ ị ạ
a : quy đnh h t xanhị ạ
B: quy đnh v tr nị ỏ ơ
b: quy đnh v nhănị ỏ
*Xác đnh ki u gen c a b m (P):ị ể ủ ố ẹ
- Vàng, tr n thu n ch ng: AABBơ ầ ủ
- Xanh, nhăn : aabb
* S đ lai:ơ ồ
P: AABB (vàng, tr n) x aabb (xanh, nhăn)ơ
Gp: AB ab
F1: AaBb (vàng, tr n)ơ
F1 x F1: AaBb (vàng, tr n) x AaBb (vàng, tr n)ơ ơ
GF1: AB, Ab, aB, ab AB, Ab, aB, ab
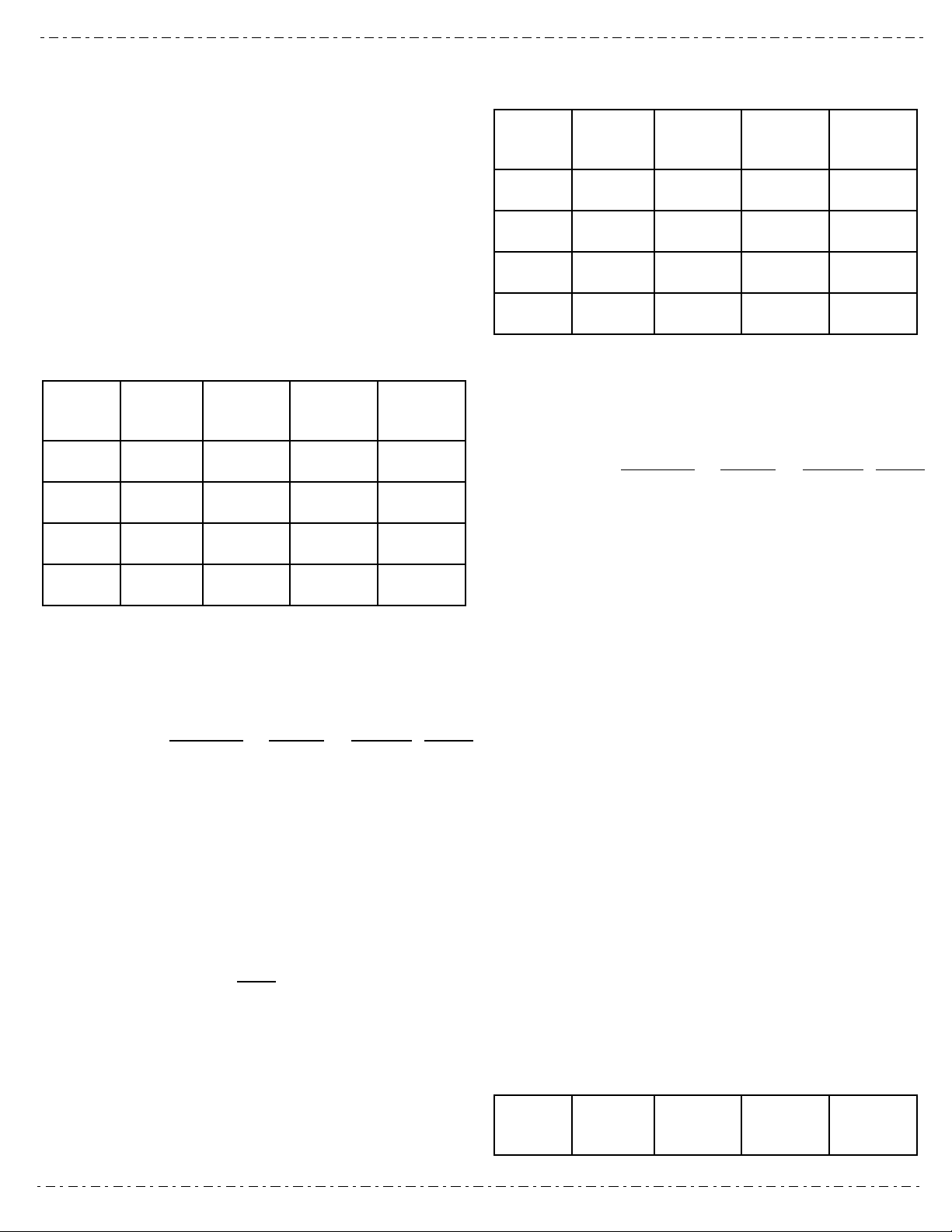
F2:
♀ ♂ AB Ab aB ab
AB AABB AABb AaBB AaBb
Ab AABb AAbb AaBb Aabb
aB AaBB AaBb aaBB aaBb
ab AaBb Aabb aaBb aabb
1AABB, 1Aabb, 1 aaBB, 1 aabb, 4 AaBb, 2AABb, 2 AaBB,
2 Aabb, 2 aaBb.
1AABB 1Aabb 1aaBB 1aabb
4A aBb 2Aabb 2aaBb
2AABb
2A aBB
- T l ki u gen: 9A – B – : 3A – bb : 3aaB – :ỉ ệ ể
1aabb
-T l KH : 9vàng,tr n:3vàng,nhăn:3xanh,tr n:1xanhỉ ệ ơ ơ
nhăn
Bài 1: đu Hà Lan, gen A: qu đ, a: qu xanh, B: quỞ ậ ả ỏ ả ả
tròn, b: qu dài. Các gen này phân li đc l p. cho cây quả ộ ậ ả
đ, tròn thu n ch ng xquar xanh, dài thu n ch ng.ỏ ầ ủ ầ ủ
a)Vi t s đ lai t P ế ơ ồ ừ
F2. Tính t l KG, KH c a F2.ỉ ệ ủ
b) N u cho Fế1 lai phân tích thì k t qu con lai nh th ế ả ư ế
nào?
Gi i:ả
a) * Quy c gen: A: qu đ, a : qu xanhướ ả ỏ ả
B: qu tròn, b: qu dàiả ả
*Xác đnh ki u gen c a b m (P):ị ể ủ ố ẹ
- Qu đ, tròn thu n ch ng: AABBả ỏ ầ ủ
- Qu xanh, dài thu n ch ng: aabbả ầ ủ
* S đ lai:ơ ồ
P: AABB (đ, tròn) x aabb (xanh, dài)ỏ
Gp: AB ab
F1: AaBb (đ, tròn)ỏ
F1 x F1: AaBb (đ, tròn) x AaBb (đ, tròn)ỏ ỏ
GF1: AB, Ab, aB, ab AB, Ab, aB, ab
F2:
♀ ♂ AB Ab aB ab
AB AABB AABb AaBB AaBb
Ab AABb AAbb AaBb Aabb
aB AaBB AaBb aaBB aaBb
ab AaBb Aabb aaBb aabb
1AABB, 1Aabb, 1 aaBB, 1 aabb, 4 AaBb, 2AABb, 2 AaBB,
2 Aabb, 2 aaBb.
1AABB 1Aabb 1aaBB 1aabb
4A aBb 2Aabb 2aaBb
2AABb
2A aBB
- T l ki u gen: 9A – B – : 3A – bb : 3aaB – :ỉ ệ ể
1aabb
-T l KH : 9đ, tròn : 3đ, dài : 3xanh, tròn : 1xanh dài.ỉ ệ ỏ ỏ
b) F1 lai phân tích F1:
AaBb (đ, tròn) x aabb ( xanh, dài)ỏ
GF1: AB, Ab, aB, ab ab
FB: AaBb , Aabb , aaBb , aabb
- T l ki u gen: 1AaBb : 1Aabb : 1 aaBb : 1 aabbỉ ệ ể
- T l KG:1 đ , tròn : 1 đ, dài : 1 xanh, tròn : 1 xanh, ỉ ệ ỏ ỏ
dài
Bài 2: lúa thân th p tr i hoàn toàn so v i thân cao, h tỞ ấ ộ ớ ạ
chín s m tr i hoàn toàn v i h t chín mu nớ ộ ớ ạ ộ
Cho cây lúa thu n ch ng có thân th p, h t chín mu n ầ ủ ấ ạ ộ
giao ph i v i cây thu n ch ng có thân cao, h t chín s m ố ớ ầ ủ ạ ớ
F1 : Vi t s đ lai t P ế ơ ồ ừ F2
Lai phân tích F1 thì k t qu nh th nào?ế ả ư ế
Gi iả
* Quy c gen: A là thân th p, a là thân caoướ ấ
B: h t chín s m, b : h t chín mu nạ ớ ạ ộ
* S đ lai:ơ ồ
P:Aabb(thân th p,chín mu n) x aaBB(thân cao,chín ấ ộ
s m)ớ
Gp: Ab aB
F1: AaBb(toàn thân th p, h t chín s m)ấ ạ ớ
F1 x F1: AaBb(thân th p,chín s m) x AaBb (thân th p,ấ ớ ấ
chín mu n)ộ
GF1: AB, Ab, aB, ab AB, Ab, aB, ab
F2:
♀ ♂ AB Ab aB ab
Đ Ng c Hoàng Hânỗ ọ 2

AB AABB AABb AaBB AaBb
Ab AABb AAbb AaBb Aabb
aB AaBB AaBb aaBB aaBb
ab AaBb Aabb aaBb aabb
1AABB, 1Aabb, 1 aaBB, 1 aabb, 4 AaBb, 2AABb, 2 AaBB,
2 Aabb, 2 aaBb.
1AABB 1Aabb 1aaBB 1aabb
4A aBb 2Aabb 2aaBb
2AABb
2A aBB
- T l ki u gen: 9A – B – : 3A – bb : 3aaB – :ỉ ệ ể
1aabb
- T l KH:9th p, s m: 3th p, mu n:3cao,mu n: 1cao ỉ ệ ấ ớ ấ ộ ộ
th pấ
Lai phân tích F1:
AaBb( th p, s m) x aabb(cao, mu n) ấ ớ ộ
GF1: AB, Ab, aB, ab ab
FB: AaBb , Aabb , aaBb , aabb
- T l ki u gen: 1AaBb : 1Aabb : 1 aaBb : 1 aabbỉ ệ ể
- T l KG:1th p, s m:1th p, mu n:1cao, mu n:1cao, ỉ ệ ấ ớ ấ ộ ộ
s mớ
P: AABB x aabb
Gp: AB ab
F1: AaBb
P;; AaBB x aabb
Gp: AB, aB ab
F1: AaBb aaBb
P: AaBb x aabb
Gp: AB, Ab, aB, ab ab
F1: FB: AaBb , Aabb , aaBb , aabb
Đ Ng c Hoàng Hânỗ ọ 3
















