Nguyn Tt Thu http//:www.maths.vn
Trưng THPT Lê Hng Phong – Biên Hòa – ðng Nai - 1 -
CHƯƠNG VII
BÀI TOÁN LIÊN QUAN ðN THAM S
Khi gii các bài toán v phương trình, bt phương trình, h phương trình ta thưng
hay gp các bài toán liên quan ñn tham s. Có l ñây là dng toán mà nhiu hc
sinh lúng túng nht. Trong chương này chúng ta s ñi nghiên cu mt s dng toán
mà chúng ta thương hay gp (như xác ñnh tham s ñ phương trình có nghim, có
k nghim, nghim ñúng vi mi x thuc tp D nào ñó… ) và phương pháp gii các
dng toán ñó.
1. Phương pháp hàm s
Bài toán 1: Tìm ñiu kin ca tham s ñ phương trình f(x)=g(m) có nghim
trên D
Phương pháp: Da vào tính cht phương trình có nghim
⇔
hai ñ th ca
hai hàm s
(
)
y f x
=
và
(
)
y g m
=
ct nhau. Do ñó ñ gii bài toán này ta tin
hành theo các bưc sau:
1) Lp bng bin thiên ca hàm s
(
)
y f x
=
.
2)
Da vào bng bin thiên ta xác ñnh m ñ ñưng thng
(
)
y g m
=
ct ñ
th hàm s
(
)
y f x
=
.
Chú ý : Nu hàm s
(
)
y f x
=
liên tc trên D và
m min f (x)
∈
=
, x D
M Max f (x)
∈
=
thì
ph
ươ
ng trình :
(
)
f x k
=
có nghi
m khi và ch
khi
m k M.
≤ ≤
Ví d 1:
Tìm m
ñ
các ph
ươ
ng trình sau có nghi
m
2 2
42
1) x x 1 x x 1 m
2) x 1 x m
+ + − − + =
+ − =
.
Gii:
1)Xét hàm s
2 2
f (x) x x 1 x x 1
= + + − − +
có tp xác ñnh là D=R.
Ta có: 2 2
2x 1 2x 1
f '(x)
2 x x 1 2 x x 1
+ −
= −
+ + − +
( ) ( )
2 2
f ' x 0 (2x 1) x x 1 2x 1 x x 1 (1)
⇒= ⇔ + − + = − + +
2 2
2 2
1 1 3 1 1 3
x [(x ) ] x [(x ) ] x 0
2 2 4 2 2 4
⇒+ − + = − + + ⇔ =
thay vào (1) ta th
y
không th
a mãn. V
y ph
ươ
ng trình
f '(x) 0
=
vô nghi
m
f '(x)
⇒
không
ñ
i d
u
trên R, mà
f '(0) 1 0 f (x) 0 x R f (x)
= > ⇒> ∀ ∈ ⇒
ñ
ng bi
n.
M
t khác:
2 2
x
x
2x
limf (x) lim 1
x x 1 x x 1
→+∞
→+∞
= =
+ + + − + và
x
limf (x) 1
→−∞
= −
.
B
ng bi
n thiên:
Nguyn Tt Thu http//:www.maths.vn
Trưng THPT Lê Hng Phong – Biên Hòa – ðng Nai - 2 -
x
−∞
+∞
f’(x)
+
f(x)
1
-1
Da vào bng bin thiên ta thy phương trình ñã cho có nghim
1 m 1
⇔ − < <
.
2) ðK:
x 0
≥
Xét hàm s
42
f (x) x 1 x
= + −
vi
x D [0; )
∈ = +∞
Ta có:
2 3
4
x 1
f '(x)
2 x
2 (x 1)
= −
+
.
2 3 6 2 3 2 2
4
f '(x) 0 x x (x 1) x (x 1) x x 1
⇒= ⇔ = + ⇔ = + ⇔ = +
vô nghi
m
f '(x)
⇒
không
ñ
i d
u trên D, mà
4
1 1
f '(1) 0 f '(x) 0 x D
2
2 8
= − < ⇒< ∀ ∈
M
t khác:
4
2 3 2 2 2 4 2 6
x x 4 4 4
1
lim f (x) lim 0
(x 1) x (x 1) x (x 1) x
→+∞ →+∞
= =
+ + + + + +
0 f (x) f (0) 1 x D
⇒< ≤ = ∀ ∈ ⇒
ph
ươ
ng trình có nghi
m
0 m 1
⇔ < ≤
.
Chú ý :
N
u ph
ươ
ng trình ch
ư
a có d
ng trên thì ta tìm cách cô l
p m
ñư
a v
d
ng
trên.
Ví d 2:
Tìm m
ñ
các ph
ươ
ng trình sau có nghi
m:
1)
44
x 13x m x 1 0
− + + − =
.
2)
x x x 12 m( 5 x 4 x )
+ + = − + −
.
Gii:
1) Phương trình 44
4 2
x 1
x 13x m 1 x
x 13x m (1 x)
≤
⇔ − + = − ⇔ − + = −
3 2
x 1
4x 6x 9x 1 m
≤
⇔
− − = −
. Xét hàm s
3 2
f (x) 4x 6x 9x
= − −
vi
x 1
≤
Ta có:
2
3
x
2
f '(x) 12x 12x 9 f '(x) 0
1
x
2
=
= − −
⇒
= ⇔
= −
.
Bng bin thiên:
x
−∞
1 / 2
−
1
f’(x) + 0 –
f(x)
5
2
−∞
11
−
Nguyn Tt Thu http//:www.maths.vn
Trưng THPT Lê Hng Phong – Biên Hòa – ðng Nai - 3 -
Da vào bng bin thiên suy ra phương trình có nghim
5 3
1 m m
2 2
⇔ − ≤ ⇔ ≥ −
.
2) ðiu kin:
0 x 4
≤ ≤
.
Khi ñó phương trình
f (x) (x x x 12)( 5 x 4 x) m
⇔ = + + − − − =
(Vì
5 4 0
x x
− − − ≠
)
Xét hàm s
f (x) (x x x 12)( 5 x 4 x )
= + + − − −
v
i
0 x 4
≤ ≤
.
Ta có:
3 1 1 1
f '(x) ( x )( )
2
2 x 12 2 4 x 2 5 x
= + −
+ − −
.
Do
1 1
0 4 x 5 x 0 f '(x) 0 x [0;4)
2 4 x 2 5 x
< − < − ⇒− > ⇒> ∀ ∈
− −
.
V
y f(x) là hàm
ñ
ng bi
n trên [0;4]
2 3( 5 2) f (0) f (x) f (4) 12
⇒
− = ≤ ≤ =
Suy ra ph
ươ
ng trình có nghi
m
2 3( 5 2) m 12.
⇔ − ≤ ≤
Chú ý :
Khi g
p h
ph
ươ
ng trình trong
ñ
ó m
t ph
ươ
ng trình c
a h
không ch
a
tham s
thì ta s
ñ
i gi
i quy
t ph
ươ
ng trình này tr
ư
c. T
ph
ươ
ng trình này ta s
tìm
ñư
c t
p nghi
m
x D
∈
(
ñ
i v
i h
m
t
!
n) ho
c s
rút
ñư
c
!
n này qua
!
n kia.
Khi
ñ
ó nghi
m c
a h
ph
thu
c vào nghi
m c
a ph
ươ
ng trình th
hai v
i k
t qu
ta tìm
ñư
c
"
trên.
Ví d 3:
Tìm m
ñ
h
sau có nghi
m:
24 5x
x
2
1
2 (1)
2
3x mx x 16 0 (2)
−
≤
− + =
.
Gii:
Ta thy (1) là bt phương trình mt !n nên ta s ñi gii bt phương trình này
Ta có: 2
x 5x 4 2 2
2 2 x 5x 4 x 5x 4 0 1 x 4
−
≤ ⇔ ≤ − ⇔ − + ≤ ⇔ ≤ ≤
.
H
có nghi
m
(2)
⇔
có nghi
m
x [1;4]
∈
.
2
3x 16
(2) m
x x
+
⇔ =
. Xét hàm s
2
3x 16
f (x)
x x
+
=
v
i
x [1;4]
∈
có
2 2 2
3 3
3
6x x x(3x 16) 3 x(x 16)
2
f '(x) 0 x [1;4]
x 2x
− + −
= = ≤ ∀ ∈
.
8 f (4) f (x) f (1) 19 x [1;4]
⇒
= ≤ ≤ = ∀ ∈
.
V
y h
có nghi
m
8 m 19
⇔ ≤ ≤
.
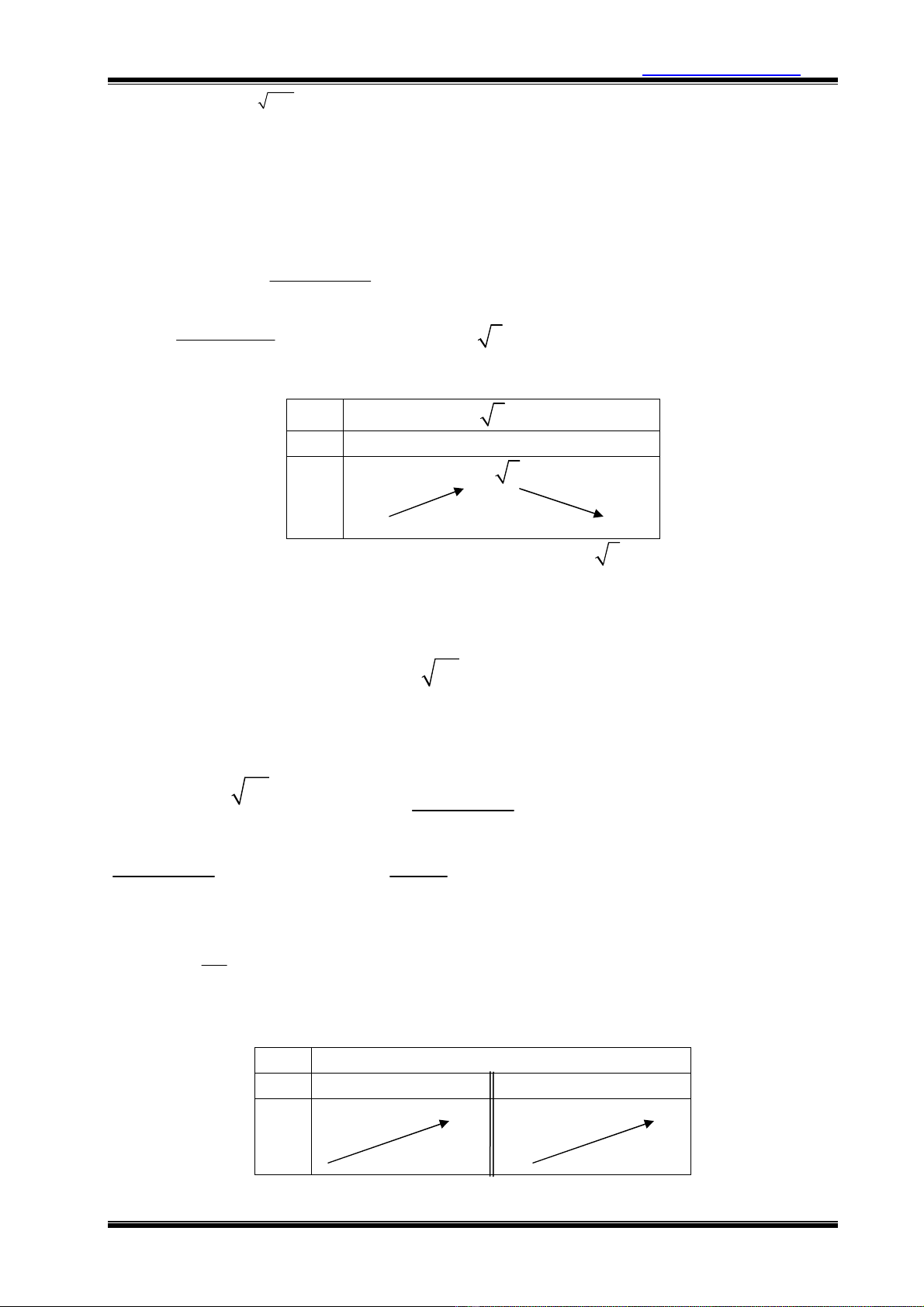
Ví d 4: Tìm m ñ h sau có nghim:
2x x 1 2 x 1
2
7 7 2007x 2007 (1)
x (m 2)x 2m 3 0 (2)
+ + + +
− + ≤
− + + + =
.
Gii:
Nguyn Tt Thu http//:www.maths.vn
Trưng THPT Lê Hng Phong – Biên Hòa – ðng Nai - 4 -
Ta có:
2 x 1 2(x 1)
(1) 7 (7 1) 2007(1 x) (3)
+ + −
⇔ − ≤ −
.
• Nu
x 1 VT(3) 0 VP(3) (3)
>⇒> > ⇒
vô nghim.
• Nu
x 1 VT(3) 0 VP(3) (3)
≤⇒≤ ≤ ⇒
ñúng
(3)
⇒
có nghim
x 1
≤
.
Suy ra h có nghim
(2)
⇔
có nghim
x 1
≤
.
Ta có:
2
x 2x 3
(2) m f (x)
x 2
− +
⇔ = =
−
. Xét hàm s f(x) vi
x 1
≤
, có:
2
2
x 4x 1
f '(x) f '(x) 0 x 2 3
(x 2)
− +
=⇒= ⇔ = −
−
.
Bng bin thiên
x
−∞
2 3
− 1
f’(x)
+ 0 –
f(x)
2 2 3
−
−∞
2
−
D
a vào b
ng bi
n thiên
⇒
h
có nghi
m
m 2 2 3
⇔ ≤ − .
Ví d 5:
Tìm m
ñ
h
ph
ươ
ng trình sau có nghi
m:
2x y m 0 (1)
y xy 2 (2)
− + =
+ =
.
Gii:
Ta thy (2) là phương trình không cha tham s nên ta s gii quyt (2) trưc
Ta có: 2
y 2
(2) xy 2 y
y 4y 4
xy
≤
⇔ = − ⇔
− +
=
. Thay vào (1) ta ñư c:
2
y 4y 4 4y 4
y m 0 m f (y)
y y
− + −
− + = ⇔ = =
(3).
H có nghim
(3)
⇔
có nghim
y 2
≤
. Xét hàm s f(y) vi
y 2
≤
2
4
f '(y) 0 f (y)
y
⇒= > ⇒
ñng bin trên các khong
( ;0) (0;2]
−∞ ∪
yy 0 y 0
lim f (y) 4; lim f (y) ; lim f (y)
+ −
→−∞ → →
= = −∞ = +∞
. Ta có bng bin thiên:
y
−∞
0 2
f’(y)
+ +
f(y)
+∞
2
4
−∞
⇒
h có nghim
m ( ;2] (4; )
⇔ ∈ −∞ ∪ +∞
.
Nguyn Tt Thu http//:www.maths.vn
Trưng THPT Lê Hng Phong – Biên Hòa – ðng Nai - 5 -
Chú ý : Khi bài toán yêu c#u xác ñnh s nghim ca phương trình thì ta phi lưu ý
S nghim ca phương trình
f (x) g(m)
=
chính là s giao ñim ca ñ th hai hàm
s
y f (x)
=
và
y g(m)
=
. Do ñó phương trình có k nghim
⇔
hai ñ th trên ct
nhau ti k giao ñim.
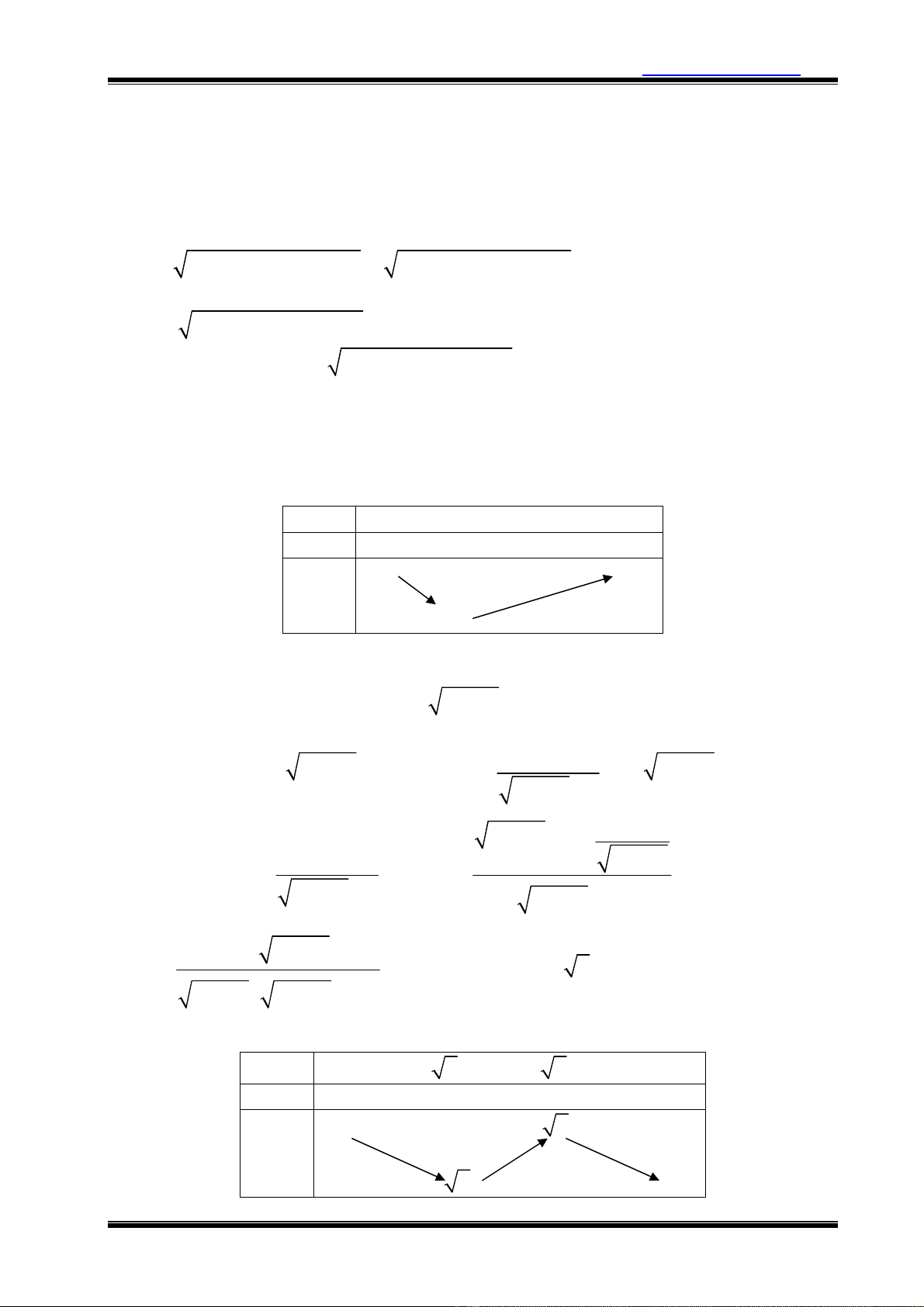
Ví d 6: Tìm tt c các giá tr ca m ñ phương trình sau có ñúng hai nghim phân
bit:
4
4 3 4 3
x 4x 16x m x 4x 16x m 6
− + + + − + + =
.
Gii:
ðt 44 3
t x 4x 16x m, t 0
= − + + ≥
. Ta có phương trình :
4
2 4 3
t t 6 0 t 2 x 4x 16x m 2
+ − = ⇔ = ⇔ − + + =
4 3
m x 4x 16x 16
⇔ − = − + −
. Xét hàm s
4 3
f (x) x 4x 16x 16
= − + −
3 2 2
x 1
f '(x) 4(x 3x 4) 4(x 2) (x 1) f '(x) 0
x 2
= −
⇒= − + = − + ⇒= ⇔
=
.
B
ng bi
n thiên
x
−∞
-1
2
+∞
f’(x) – 0 + 0 +
f(x)
+∞
+∞
-27
D
a vào b
ng bi
n thiên
⇒
ph
ươ
ng trình có hai nghi
m phân bi
t
m 27 m 27
⇔ − > − ⇔ <
.
Ví d 7: Tìm m ñ phương trình : 2
m x 2 x m
+ = +
có ba nghi
m phân bi
t.
Gii:
Phương trình 2
2
x
m( x 2 1) x m
x 2 1
⇔ + − = ⇔ =
+ −
(do 2
x 2 1 0 x
+ − > ∀
)
Xét hàm s
( )
2
2
2
2
22
x
x 2 1
x
x 2
f (x) f '(x)
x 2 1 x 2 1
+ − −
+
=⇒=
+ − + −
( )
2
2
2 2
2 x 2
f '(x) f '(x) 0 x 2
x 2 x 2 1
− +
=⇒= ⇔ = ±
+ + −
.
B
ng bi
n thiên:
x
−∞
2
−
2
+∞
f’(x)
–
0 +
0
–
f(x)
+∞
2
2
−
−∞