TRƯỜNG ĐẠI HỌC TÀI CHÍNH - MARKETING
BỘ MÔN TOÁN – THỐNG KÊ
Slide bài giảng và bài tập
MÔN KINH TẾ LƯỢNG
(Econometric)
Giảng viên : ThS. Nguyễn Trung Đông
Tp. Hồ Chí Minh, 02 - 02 - 2014
1
1
TRƯỜNG ĐẠI HỌC
TÀI CHÍNH - MARKETING
KHOA CƠ BẢN
Môn : KINH TẾ LƯỢNG
(Econometric)
Số tín chỉ : 3
Số tiết : 30 LT + 30 TH
Giảng viên : ThS. Nguyễn Trung Đông
2
TRƯỜNG ĐẠI HỌC
TÀI CHÍNH - MARKETING
KHOA CƠ BẢN
Moân : KINH TẾ LƯỢNG
(Econometric)
Hình thức đánh giá môn học
Điểm quá trình (30%)
Điểm kết thúc học (70%)
Điểm học phần = (Điểm quá trình + Điểm kết thúc học)
Giảng viên : ThS. Nguyễn Trung Đông
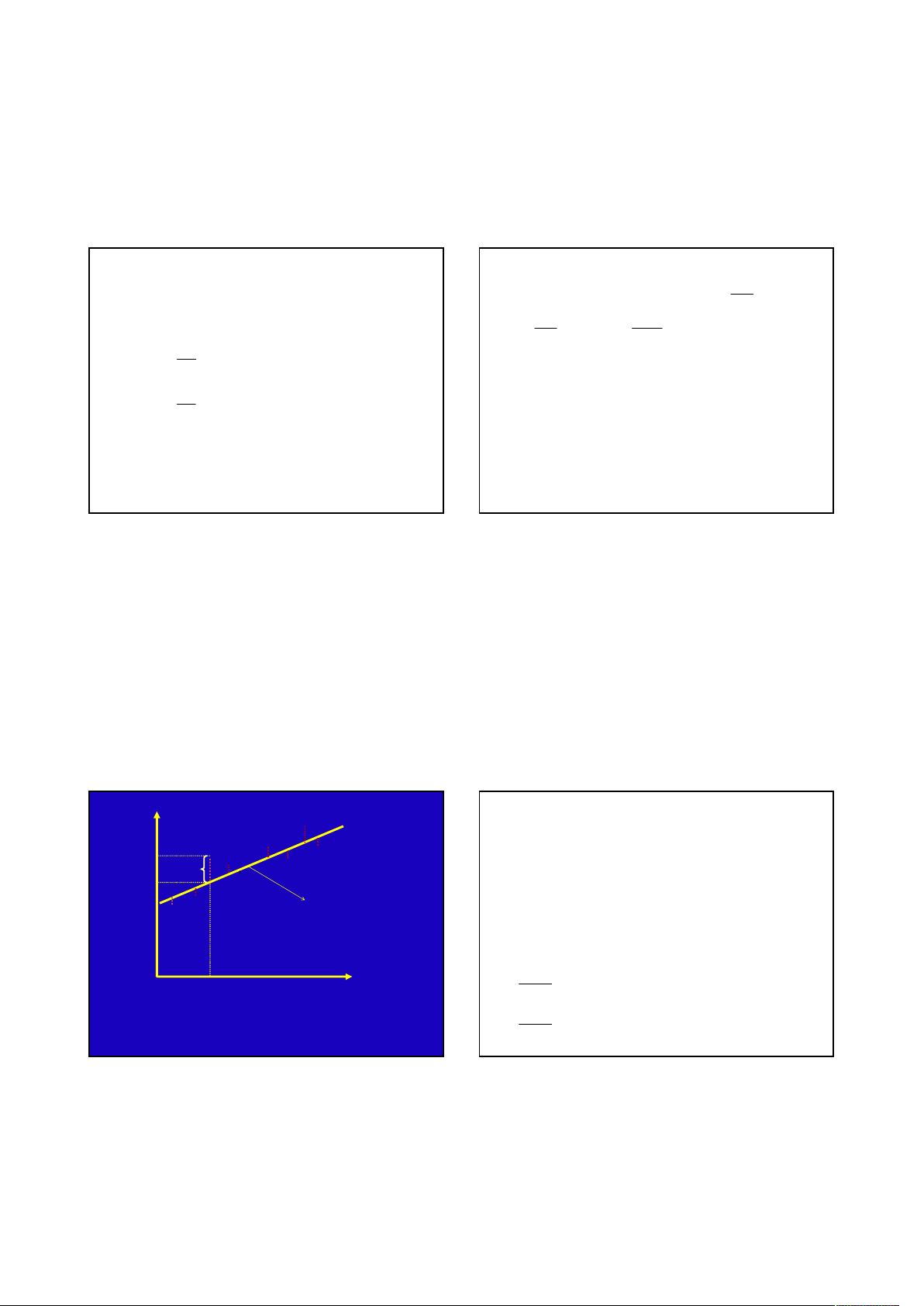
TỔNG QUAN
Mục tiêu môn học:
Cung cấp phương pháp phân tích định
lượng.
Ứng dụng: Phương pháp định lượng
Làm thực tập tốt nghiệp, luận văn tốt
nghiệp.
Phân tích, kiểm định và dự báo kinh tế.
3
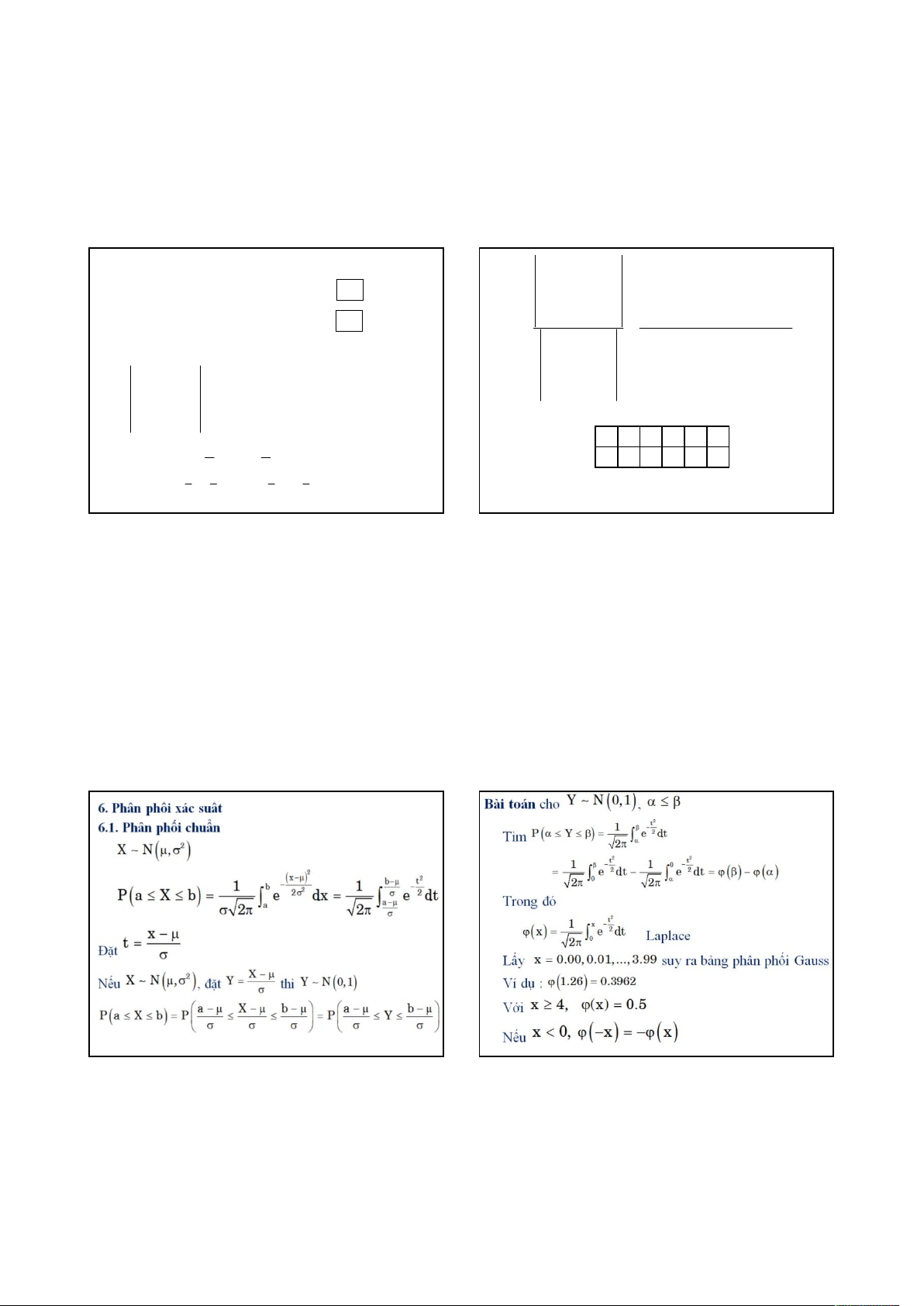
NỘI DUNG MÔN HỌC
Ôn tập
Chương 0. Mở đầu
Chương 1. Hồi quy hai biến
Chương 2. Hồi quy bội
Chương 3. Kiểm định giả thuyết
mô hình
4
TÀI LIỆU THAM KHẢO
Tiếng Việt
1) Đinh Ngọc Thanh, Nguyễn Văn Phong, Nguyễn Trung
Đông, Nguyễn Thị Hải Ninh: Giáo trình kinh tế lượng,
lưu hành nội bộ, Đại học tài chính – Marketing.
2) Phạm Chí Cao – Vũ Minh Châu: Kinh tế lượng ứng
dụng, nhà xuất bản Thống kê, 2010.
3) Nguyễn Quang Dong: Bài giảng Kinh tế lượng, nhà
xuất bản thống kê, 2006.
4) Chương trình giảng dạy Kinh tế Fullbright: Bài giảng
Kinh tế lượng, 2004.
5) Huỳnh Đạt Hùng, Nguyễn Khánh Bình, Phạm Xuân
Giang: Kinh tế lượng, nhà xuất bản Phương Đông, 2012.
5 6
6) Nguyễn Cao Văn – Bùi Dương Hải, Kinh tế lượng
(hướng dẫn và trả lời lý thuyết và bài tập, nhà xuất bản
Tài Chính.
7) Bùi Minh trí: Kinh tế lượng, nhà xuất bản khoa học
và kỹ thuật, 2006.
Tiếng Anh
1) Dimitrios Asteriou and Stephen G. Hall: Applied
Econometrics, Published by Palgrave Macmillan, 2007.
2) Christopher Dougherty: Introduction to
Econometrics, Published Oxford.
3) Jeffrey M. Wooldridge: Introduction to
Econometrics,…
4) Damodar N Gujatari, Basic Econometrics, Mc Graw
– Hill Inc, third edition, 1995.
21/01/2014
1
Chương 0.
Ôn Tập
Kinh tế lượng (Econometic): Lượng hóa các
vấn đề về kinh tế.
1. Đạo hàm (tỷ lệ sự thay đổi)
Xét hàm số Y=f(X). Trong đó
Y : Biến phụ thuộc, biến được giải thích,
biến nội sinh, biến hồi quy.
X : Biến độc lập, biến giải thích, biến
ngoại sinh.
Ví dụ 1: Thu nhập (X) – Chi tiêu (Y).
Lạm phát (X) – Lãi suất (Y).
2. Đạo hàm tại điểm. Xét hàm số:
Sự thay đổi của y theo x:
Tỷ lệ sự thay đổi của y theo x xung quanh
điểm a.
Ví dụ 2: Xét mối quan hệ:
Giả sử: x: lạm phát, y: lãi suất và
Ý nghĩa: Nếu LP tăng 1% thì LS tăng 1.25%.
f (x) f (a) y
x a x
y f (x)
/ /
y f (a) y / x
x
y f (x)
/
f (5) 1.25
: sự thay đổi của y
y
: sự thay đổi của x
3. Đạo hàm riêng. Xét hàm số:
z : là biến phụ thuộc (biến được giải thích)
x,y : là biến độc lập (biến giải thích)
3.1. Đạo hàm riêng của z theo x
3.2. Đạo hàm riêng của z theo y
z z
(3,2) 0.4; (3,2) 0.1
x y
x 0
z f (x x, y) f (x, y)
lim ; ( x, y 0)
x x
y 0
z f (x, y y) f (x, y)
lim ; ( x 0, y)
y y
Ví dụ 3:
4
Ví dụ 4: Tính đạo hàm riêng của hàm số sau
3 3
2 2
1. f (x,y) x y 6xy 2x 3y 1
2. f (x, y) ln(x y )
2 2
2 2 2 2
f f
1. (x, y) 3x 6y 2; (x,y) 3y 6x 3
x y
f 2x f 2y
2. (x, y) ; (x, y)
x x y y x y
Giải
21/01/2014
2
4. Điều kiện cần của cực trị.
Xét hàm số:
Hàm số đạt cực trị tại
0 0
(x , y )
0 0
0 0
f(x ,y ) 0
x
(*)
f(x ,y ) 0
y
Nếu thỏa (*) thì được gọi
là điểm dừng.
0 0
(x , y )
0 0
(x , y )
Th1: Nếu và thì là cực tiểu.
5. Điều kiện đủ của cực trị.
Xét điểm dừng: . Đặt
2
0 0
2
f
A (x ,y ),
x
0 0
(x , y )
0
A 0
2 2
2
0 0 0 0
2
f f
C (x , y ), B (x , y ), AC B
y x y
0 0
(x , y )
Th2: Nếu và thì là cực đại.
Th3: Nếu thì không là cực trị.
Th4: Nếu chưa đủ cơ sở kết luận.
0
0
0
A 0
0 0
(x , y )
0 0
(x , y )
Y
.
.
..
.
.
..
.
.
.
e
i
XX
i
Y
i
.
..
.
.
0
SRF
i
Y
7
Khi
i1 2
i i i i i
X X e Y Y Y X
i1 2
i
Y X
8


n
1 2 1 2
i i
i 1
1
n
1 2 1 2
i i i
i 1
2
RSS
, 2 Y X ( 1) 0
RSS
, 2 Y X ( X ) 0
Phương pháp bình phương cực tiểu
(OLS : Ordinary least squaes)
Tổng bình phương các sai lệch
(RSS : Residual sum of squares)
n n
2
2 2 2 2
1 2
1 2 n i i i
i 1 i 1
RSS e e ... e e Y X
Bài toán. Tìm sao cho
1 2
,
RSS min
21/01/2014
3
9
Suy ra
n n
1 2
i i
i 1 i 1
n n n
2
1 2
i i i i
i 1 i 1 i 1
n X Y
X X X Y
Hệ Cramer
n
in n
2i 1
i i
n n i 1 i 1
2
i i
i 1 i 1
n X
n X X 0
X X
n n
1 2
i i
i 1 i 1
1 1
(1) X Y
n n
1 2 1 2
X Y Y X
1
2
10
n
i
i 1
n n n
n n
i i i i
i i i i 1 i 1 i 1
i 1 i 1
22
nn n
2
ii i
i 1 i 1 i 1
n n
2
i i
i 1 i 1
n Y
n X Y X Y
X X Y
n X n X X
X X
Ví dụ:
X
1 2
3
4
5
Y
2 5
7
8
9
11 12