Báo cáo khoa học: "Một số kết quả nghiên cứu dao động uốn phi tuyến của cầu dây văng chịu tác dụng của hoạt tải khai thác"

Chia sẻ: Nguyễn Phương Hà Linh Nguyễn Phương Hà Linh | Ngày: | Loại File: PDF | Số trang:12

Thêm vào BST

Báo xấu

95
lượt xem 18
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài báo giới thiệu một số kết quả nghiên cứu mô hình bài toán dao động uốn của cầu dây văng chịu tác dụng của đoàn tải trọng ôtô di động có xét tới ảnh h-ởng của các tham số phi tuyến. Kết quả nghiên cứu đ-ợc đối chiếu với kết quả tính toán theo mô hình bài toán dao động đàn hồi tuyến tính t-ơng ứng và kết quả thực nghiệm tại một số công trình cầu dây văng trên thực tế....

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Báo cáo khoa học: "Một số kết quả nghiên cứu dao động uốn phi tuyến của cầu dây văng chịu tác dụng của hoạt tải khai thác"

Mét sè kÕt qu¶ nghiªn cøu dao ®éng uèn phi tuyÕn cña cÇu d©y v¨ng chÞu t¸c dông cña ho¹t t¶i khai th¸c TS. Hoµng hµ Bé m«n C«ng tr×nh Giao th«ng TP - §H GTVT ThS. NguyÔn §øc Tïng Bé m«n CÇu - HÇm - §H GTVT Tãm t¾t: Bμi b¸o giíi thiÖu mét sè kÕt qu¶ nghiªn cøu m« h×nh bμi to¸n dao ®éng uèn cña cÇu d©y v¨ng chÞu t¸c dông cña ®oμn t¶i träng «t« di ®éng cã xÐt tíi ¶nh h−ëng cña c¸c tham sè phi tuyÕn. KÕt qu¶ nghiªn cøu ®−îc ®èi chiÕu víi kÕt qu¶ tÝnh to¸n theo m« h×nh bμi to¸n dao ®éng ®μn håi tuyÕn tÝnh t−¬ng øng vμ kÕt qu¶ thùc nghiÖm t¹i mét sè c«ng tr×nh cÇu d©y v¨ng trªn thùc tÕ. C¸c phÇn mÒm tÝnh to¸n VICABLE-1 vμ VINONLINE-2 cã thÓ trî gióp c«ng t¸c thiÕt kÕ vμ tÝnh to¸n kiÓm tra n¨ng lùc chÞu t¶i cña c¸c c«ng tr×nh cÇu d©y v¨ng ®ang khai th¸c. Summary: The article presents some results achieved from a study on dynamic behaviours of cable - stayed bridges under moving vehicles with regard to influences of parameters of the dynamic behaviours. The results are compared with those calculated on the corresponding model and on-spot results at some actual cable - stayed bridges. Software packages VICABLE 1 and VICABLE 2 can facilitate designing and calculating load capacity of the cable - stayed bridges in operation. I. §Æt vÊn ®Ò Trong [1] ®· nghiªn cøu m« h×nh bµi to¸n dao ®éng uèn cña cÇu d©y v¨ng chÞu t¸c dông cña ®oµn t¶i träng «t« di ®éng víi giíi h¹n trong bµi to¸n dao ®éng ®µn håi tuyÕn tÝnh. KÕt qu¶ nghiªn cøu ®· cho phÐp kh¶o s¸t trong ph¹m vi réng tr¹ng th¸i dao ®éng cña kÕt cÊu nhÞp cÇu d©y v¨ng víi s¬ ®å cÇu ®a d¹ng chÞu t¸c dông cña ®oµn xe t¶i cã sè l−îng, t¶i träng, vËn tèc vµ cù ly xe bÊt kú. ThuËt to¸n cïng c¸c phÇn mÒm tÝnh to¸n ®· cho c¸c kÕt qu¶ vÒ ®é vâng, øng suÊt ®éng lùc t¹i c¸c vÞ trÝ vµ ë mäi thêi ®iÓm cÇn nghiªn cøu. Ngoµi ra cßn cho c¸c gi¸ trÞ t−¬ng øng vÒ néi lùc ®éng trong c¸c d©y v¨ng hay chuyÓn vÞ ngang cña th¸p cÇu t¹i c¸c ®iÓm neo d©y. Tuy nhiªn, néi dung nghiªn cøu nªu trªn cßn ch−a ®Ò cËp ®Õn mét sè vÊn ®Ò liªn quan, trong ®ã cã ¶nh h−ëng cña c¸c yÕu tè phi tuyÕn ®èi víi tr¹ng th¸i dao ®éng vµ c¸c hiÖu øng ®éng lùc trong hÖ. §iÒu nµy lµ nguyªn nh©n lµm cho c¸c kÕt qu¶ tÝnh to¸n lý thuyÕt vµ thùc nghiÖm cßn cã sù chªnh lÖch ë møc ®é ®¸ng kÓ (tõ 9 ®Õn 17%).
ViÖc xÐt ¶nh h−ëng cña c¸c yÕu tè phi tuyÕn nh»m n©ng thªm møc ®é tiÖm cËn thùc tÕ cña m« h×nh tÝnh to¸n, lµm c¬ së cho viÖc ph©n tÝch tr¹ng th¸i dao ®éng cña d¹ng kÕt cÊu cÇu d©y v¨ng trong thùc tÕ. II. ¶nh h−ëng cña mét sè yÕu tè phi tuyÕn trong bμi to¸n dao ®éng cÇu d©y v¨ng Nghiªn cøu c¸c c¬ hÖ phi tuyÕn trong thùc tÕ cho thÊy mét c¬ hÖ dao ®éng bÊt kú th−êng do 3 yÕu tè tæ hîp: + Khèi l−îng cña c¬ hÖ + HÖ sè c¶n cña m«i tr−êng trong ®ã c¬ hÖ dao ®éng. + HÖ sè cøng vµ gi¶m chÊn cña c¸c gèi ®ì. 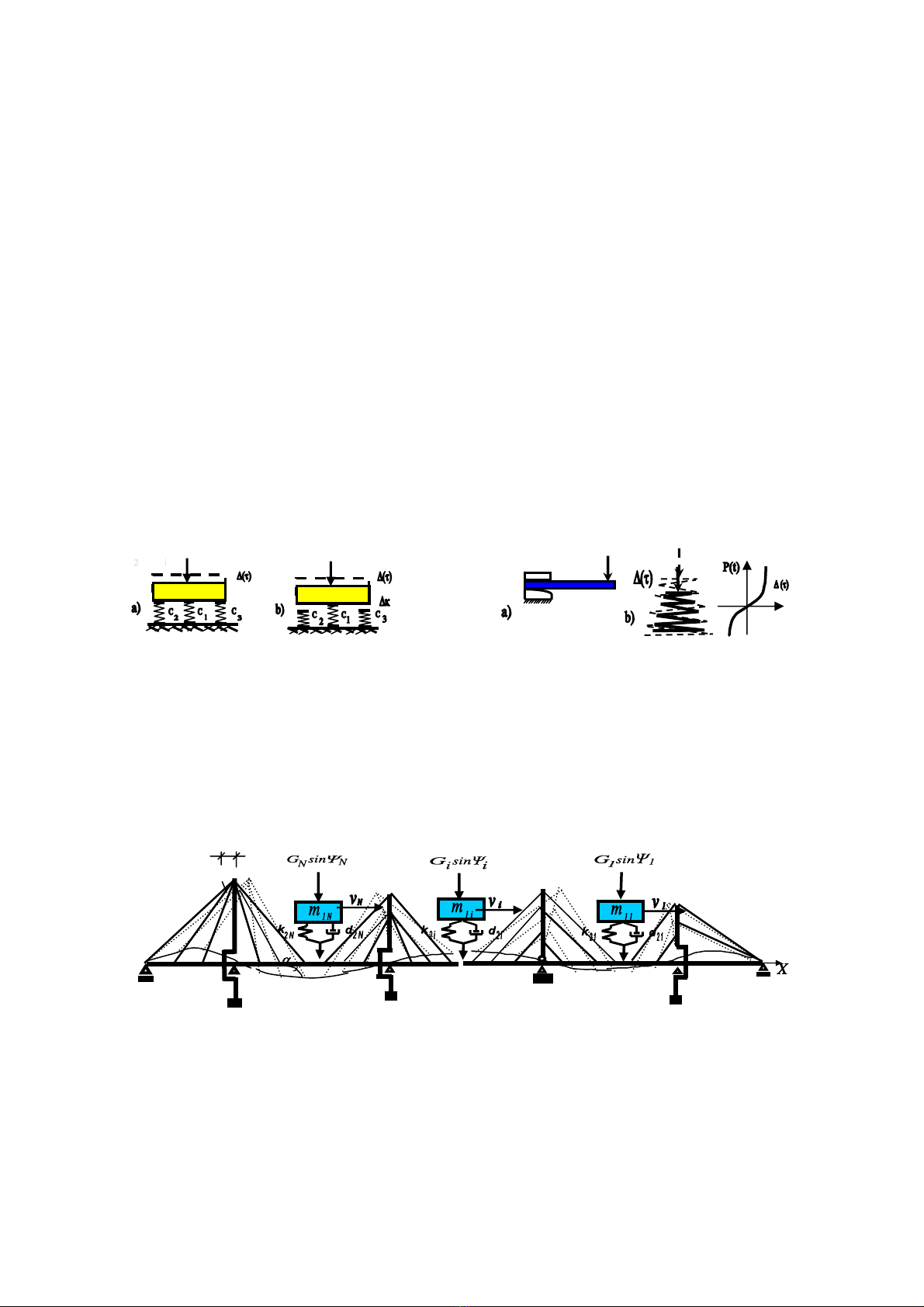TÝnh chÊt phi tuyÕn trong dao ®éng cña c¬ hÖ cã thÓ do mét, hai hay c¶ ba yÕu tè trªn quyÕt ®Þnh. M« h×nh ®¬n gi¶n nhÊt cña mét c¬ hÖ dao ®éng chÞu ¶nh h−ëng phi tuyÕn do gèi ®ì cã ®é cøng thay ®æi ®ét ngét thÓ hiÖn trªn h×nh 1b. Trong thùc tÕ cßn cã cÊu t¹o nh÷ng c¬ hÖ cã ®é cøng thay ®æi mét c¸ch liªn tôc vÝ dô nh− m« h×nh c«ng-x«n cã ®é cøng chèng uèn thay ®æi liªn tôc do cÊu t¹o ®Æc biÖt ë ngµm trªn h×nh 2a. H×nh 1. M« h×nh hÖ gèi ®ì cã ®é cøng thay ®æi ®ét ngét. H×nh 2. M« h×nh c¸c gèi ®ì cã ®é cøng thay ®æi liªn tôc Trªn h×nh 2b m« t¶ cÊu t¹o mét lß so xo¾n cã cÊu t¹o h×nh nãn côt, khi chÞu t¸c dông cña lùc P theo ph−¬ng th¼ng ®øng, c¸c vßng lß so phÝa d−íi sÏ bÞ Ðp s¸t khiÕn ®é cøng cña lß so t¨ng dÇn, ®å thÞ trªn h×nh m« t¶ quan hÖ biÕn d¹ng Δ(t) cña lß so víi lùc t¸c dông thay ®æi P(t). Theo nghiªn cøu cña §uy-phinh vµ mét sè t¸c gi¶ kh¸c quan hÖ lùc - biÕn d¹ng nªu trªn cã d¹ng mét hµm bËc 3. Dao ®éng cña kÕt cÊu nhÞp cÇu d©y v¨ng lµ tæng hîp dao ®éng cña c¬ hÖ hçn hîp gåm dao ®éng cña c¸c xe «t« vµ dao ®éng cña kÕt cÊu nhÞp cÇu d©y v¨ng (h×nh 3). X i(t) 0 H×nh 3. M« h×nh dao ®éng cña cÇu d©y v¨ng chÞu t¸c dông cña ®oμn ho¹t t¶i khai th¸c. Trong bµi to¸n dao ®éng ®µn håi tuyÕn tÝnh ®· x©y dùng m« h×nh t¶i träng xe gåm c¸c khèi l−îng ®Æt trªn c¸c lß so ®µn håi cã ®é cøng kh«ng ®æi. Nh− vËy ¸p lùc cña ho¹t t¶i truyÒn xuèng mÆt cÇu sÏ tû lÖ tuyÕn tÝnh víi ®é biÕn d¹ng theo ph−¬ng th¼ng ®øng cña nhÝp xe.
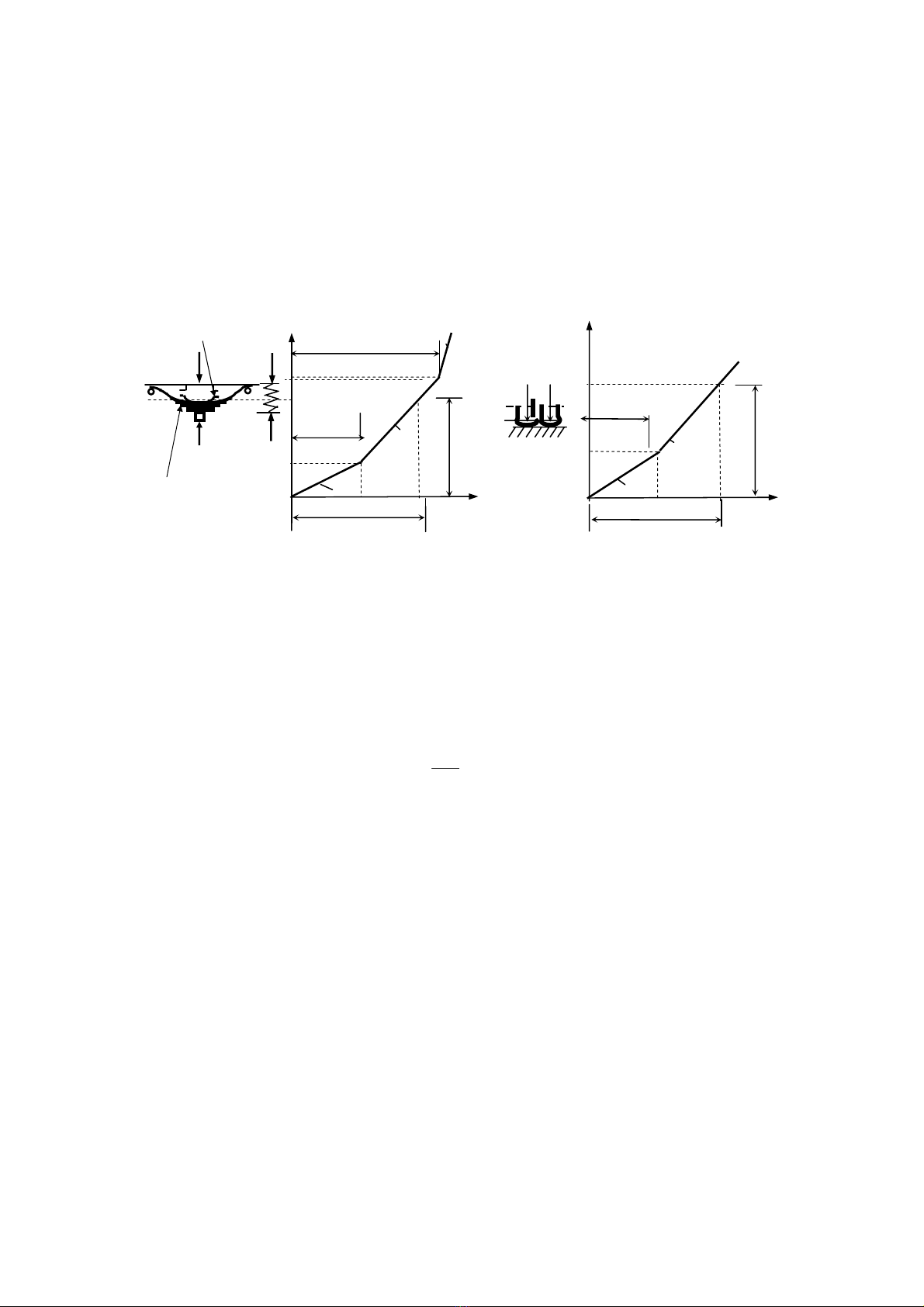
Thùc tÕ do cÊu t¹o ®Æc biÖt cña hÖ nhÝp vµ lèp xe «t«, c¸c tham sè ®é cøng cña c¸c bé phËn nµy còng thay ®æi kh«ng theo quy luËt tuyÕn tÝnh. Trªn h×nh 4 giíi thiÖu biÓu ®å thay ®æi ®é cøng cña nhÝp vµ lèp tïy thuéc vµo ®é lín cña t¶i träng t¸c dông theo ph−¬ng th¼ng ®øng vµ ®é biÕn d¹ng cña nhÝp vµ lèp cña mét sè lo¹i «t« l−u hµnh kh¸ phæ biÕn ë ViÖt Nam. Nh− vËy viÖc lÊy mét trÞ sè ®é cøng kh«ng ®æi cña nhÝp xe nh− trong bµi to¸n dao ®éng ®µn håi tuyÕn tÝnh lµ ch−a hoµn toµn phï hîp víi thùc tÕ. a) NhÝp phô F yn 2 b) R 3 k1 3 F 2 2 R yn 1 k1 2 yl 1 F(t) k21 R(t) F k11 k21 1 1 NhÝp xe yn (t) yl t) yn yl H×nh 4. BiÓu ®å quan hÖ gi÷a ®é cøng vμ ®é gi¶m chÊn cña nhÝp vμ lèp víi khèi l−îng xe vμ biÕn d¹ng cña nhÝp vμ lèp: a- cho nhÝp xe; b- cho lèp xe. §èi víi m« h×nh cña c¸c d©y v¨ng còng ®−îc gi¶ thiÕt lµ tuyÖt ®èi th¼ng, cã ®é cøng chèng biÕn d¹ng däc trôc hoµn toµn phô thuéc vµo tiÕt diÖn vµ m«®un ®µn håi cña vËt liÖu c¸p. §é cøng cña c¸c gèi ®µn håi t¹i vÞ trÝ treo d©y vµo dÇm cøng x¸c ®Þnh theo ph−¬ng ph¸p cña Ka- chu-rin víi gi¶ thiÕt ®é cøng Ci cã quan hÖ tuyÕn tÝnh víi kh¶ n¨ng chèng biÕn d¹ng däc trôc cña c¸p d©y v¨ng: E iFi Ci = sin β i (1) Si trong ®ã: Ci - ®é cøng cña gèi ®µn håi t¹i ®iÓm neo d©y v¨ng thø i; Ei, Fi, Si vµ βi - lÇn l−ît lµ m« dun ®µn håi, diÖn tÝch mÆt c¾t, ®é dµi vµ gãc nghiªng so víi ph−¬ng n»m ngang cña d©y v¨ng thø i. 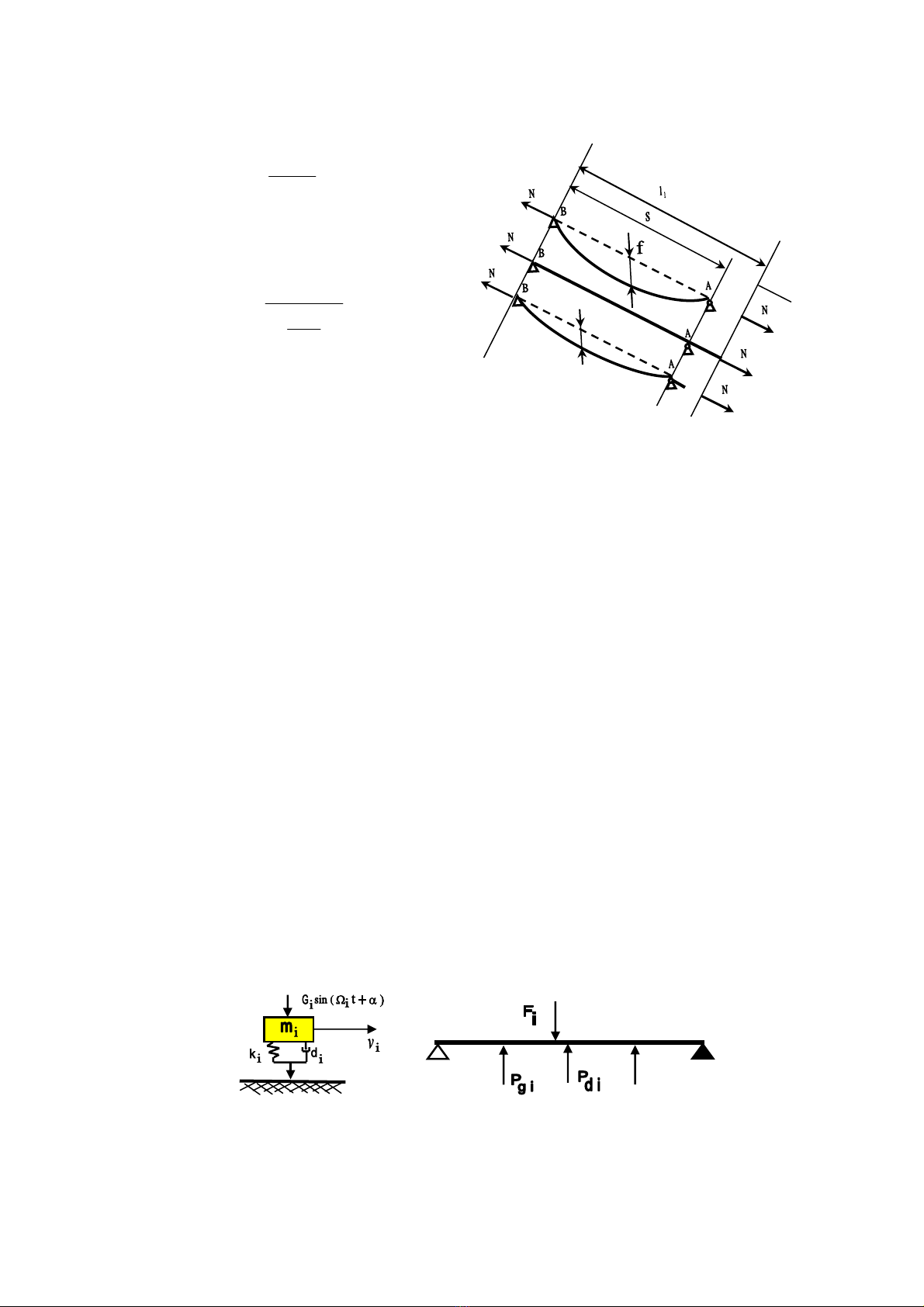Trªn thùc tÕ do t¸c dông cña t¶i träng b¶n th©n, c¸c d©y v¨ng bÞ vâng, khi chÞu t¶i träng d©y chÞu kÐo sÏ duçi th¼ng lµm thay ®æi tr¹ng th¸i øng suÊt vµ biÕn d¹ng trong toµn hÖ. VÊn ®Ò ¶nh h−ëng cña biÕn d¹ng kh«ng tuyÕn tÝnh do sù duçi th¼ng c¸c d©y v¨ng ®· ®−îc nhiÒu t¸c gi¶ quan t©m nghiªn cøu trong bµi to¸n tÜnh häc tiªu biÓu lµ c¸c c«ng tr×nh nghiªn cøu cña Gisming, Goschy, Kuder, ®Æc biÖt lµ c¸c kÕt qu¶ nghiªn cøu cña GS H.J. Ernst ®−îc coi lµ ph−¬ng ph¸p ®−îc øng dông phæ biÕn nhÊt. HÖ thøc tÝnh m«®un ®µn håi ®−îc xÐt trong mèi quan hÖ víi tæng cña hai thµnh phÇn biÕn d¹ng ®µn håi vµ biÕn d¹ng do duçi th¼ng cña d©y:
σ Ei = (2) ε f + εe TrÞ sè m« ®un ®µn håi thùc tÕ cña c¸c d©y v¨ng ®−îc sö dông kh¸i niÖm m« ®un ®µn håi t−¬ng ®−¬ng theo kiÕn nghÞ cña GS H.J. Ernst: Ee Ei = (3) (γ l )2 E 1+ σ3 e 12 trong ®ã: σ - øng suÊt trong c¸p; Ee - m«®un ®µn håi tuyÕn tÝnh cña d©y H×nh 5. v¨ng; γ - träng l−îng ®¬n vÞ cña c¸p; l - h×nh chiÕu cña c¸p trªn ph−¬ng n»m ngang. M«®un ®µn håi t−¬ng ®−¬ng sÏ phô thuéc vµo øng suÊt trong d©y v¨ng. C«ng thøc (3) cã thÓ ¸p dông cho bµi to¸n tÜnh. §èi víi bµi to¸n ®éng øng suÊt trong c¸p sÏ biÕn ®æi theo thêi gian nh− v©y m« ®un ®µn håi t−¬ng ®−¬ng còng thay ®æi theo Ei → Ei(t). HÖ qu¶ dÔ thÊy lµ ¸p lùc tõ c¸c d©y v¨ng t¸c dông lªn dÇm cøng sÏ kh«ng cã quan hÖ tuyÕn tÝnh mµ cã quan hÖ phi tuyÕn víi ®é d·n dµi cña d©y. §é cøng cña c¸c gèi ®µn håi d−íi c¸c d©y v¨ng sÏ cã tÝnh chÊt phi tuyÕn thay ®æi theo thêi gian. C¸c ph©n tÝch trªn ®©y ®· cho thÊy sù cÇn thiÕt cña viÖc ®−a vµo c¸c yÕu tè phi tuyÕn trong viÖc x©y dùng m« h×nh bµi to¸n dao ®éng cña cÇu d©y v¨ng d−íi t¸c dông cña ®oµn t¶i träng di ®éng. III. Bμi to¸n tæng qu¸t ph©n tÝch dao ®éng cÇu d©y v¨ng chÞu t¸c dông cña ho¹t t¶i khai th¸c §−êng lèi x©y dùng thuËt to¸n vµ phÇn mÒm tÝnh to¸n ®−îc tiÕn hµnh t−¬ng tù nh− ®· thùc hiÖn ®èi víi bµi to¸n dao ®éng ®µn håi tuyÕn tÝnh tr−íc ®©y. 1. X©y dùng m« h×nh hÖ dao ®éng ¸p dông ph−¬ng ph¸p c¸c cÊu tróc con ®Ó ph©n tÝch c¬ hÖ dao ®éng trªn h×nh 3 thµnh (N + 1) cÊu tróc con thÓ hiÖn trªn h×nh 6. Trong ®ã cÊu N cÊu tróc con biÓu thÞ c¸c t¶i träng di ®éng, cÊu tróc con thø (N +1) lµ dÇm cøng trong cÇu d©y v¨ng cã chiÒu dµi l . Khi t¸ch hÖ thµnh c¸c cÊu tróc con sÏ chó ý ®Õn ®iÒu kiÖn c©n b»ng cña ¸p lùc vµ chuyÓn vÞ t¹i c¸c ®iÓm liªn kÕt gi÷a chóng. H×nh 6: Ph©n tÝch hÖ dao ®éng thμnh c¸c cÊu tróc con.
§iÒu kiÖn tån t¹i cña t¶i träng thø i trªn kÕt cÊu ®−îc thÓ hiÖn th«ng qua hµm tÝn hiÖu ®iÒu khiÓn l«gÝc ξi (t) x¸c ®Þnh bëi hÖ thøc: ⎧ 1 khi τ i ≤ t ≤ τ i + Ti ⎪ ξ i ( t) = ⎨ (4) ⎪ 0 khi t 〈 τ i vµ t 〉 τ i + Ti ⎩ Fi tÝnh theo c¸c c«ng thøc: ¸p lùc cña c¸c t¶i träng di ®éng (ho¹t t¶i) lªn dÇm + §èi víi m« h×nh dao ®éng ®µn håi tuyÕn tÝnh: Fi = k i y i + di y i = mi g + Gi sin Ψi − mi && i & (5) z + §èi víi m« h×nh dao ®éng cã xÐt ®Õn yÕu tè phi tuyÕn cña nhÝp vµ lèp xe: Fi = k i y i + λ i y i3 + d i y i = mi g + Gi sin Ψi − mi && i & (6) z ¸p lùc tËp trung cña c¸c t¶i träng di ®éng Fi cã thÓ biÓu diÔn nh− mét ¸p lùc ph©n bè víi c−êng ®é p(x, zi, t) trong kho¶ng [v i (t − τi ) − ε;i (t − τi ) + ε;] vµ cã c−êng ®é b»ng kh«ng ë ngoµi kho¶ng ®ã qua hµm §en-ta-§ir¨c: p ( x, z i , t) = Fi δ( x − ηi ) ; ηi = v i (t − τ i ) (7) ViÖc thay thÕ mét lùc tËp trung b»ng lùc ph©n bè trong c¬ hÖ cã ®−îc nhê tÝnh chÊt cña hµm §en-ta-§ir¨c trong to¸n häc: p( x, z i , t) = Fi δ(x − ηi ) = lim Fi δ ε (x − ηi ) ε →0 ⎧1 x − ηi 〈ε khi ⎪ δ ε ( x − η i ) = ⎨ 2ε (8) víi ⎪0 x − ηi ≥ε khi ⎩ trong ®ã ε lµ sè d−¬ng cã thø nguyªn chiÒu dµi. 2. Thμnh lËp vμ gi¶i hÖ ph−¬ng tr×nh vi ph©n dao ®éng ¸p dông nguyªn lý ®’Alembert thµnh lËp ph−¬ng tr×nh vi ph©n dao ®éng cho c¸c cÊu tróc con. KÕt qu¶ thu ®−îc hÖ ph−¬ng tr×nh vi ph©n hçn hîp gåm N ph−¬ng tr×nh vi ph©n th−êng vµ 1 ph−¬ng tr×nh vi ph©n ®¹o hµm riªng: ⎛ ∂2W ∂W ⎞ ⎛ ∂4W ∂5W ⎞ EJ d ⎜ 4 + θ 4 ⎟ + ρFd ⎜ 2 + β ⎟ = p * ( x, z, t) (9) ⎜ ∂t ∂t ⎟ ⎜ ∂x ⎟ ∂x ∂t ⎠ ⎝ ⎠ ⎝ & ξ i ( t) [ m i && i + d i z 1i + k i z i + λ i z i3 ] = ξ i ( t) [ m i g +G i sin Ψi + d i Wηi + k i Wηi + λ i Wηi ] 3 & z (i = 1 ..N) (10) Trong hÖ ph−¬ng tr×nh hçn hîp trªn, c¸c yÕu tè phi tuyÕn do ®é vâng cña c¸c d©y v¨ng sÏ ®−îc ®−a vµo vÕ ph¶i cña ph−¬ng tr×nh (10) d−íi d¹ng biÓu thøc m« t¶ ¸p lùc ®éng tõ c¸c d©y
v¨ng lªn dÇm cøng lµ mét hµm bËc ba cña trÞ sè ®é vâng ®éng lùc cña dÇm cøng t¹i ®iÓm liªn kÕt víi d©y v¨ng: Pg ( t) = φ i Wi ( t) + φ LH Wi3 ( t) (11) i YÕu tè phi tuyÕn cña t¸c ®éng do c¸c t¶i träng g©y ra cho dÇm còng ®−îc m« t¶ th«ng qua ¸p lùc ®éng theo thêi gian cña t¶i träng lªn dÇm biÕn ®æi theo quy luËt cña hµm bËc ba: Fi ( t) = d i ( Wηi − z i ) + k i ( Wηi − z i ) + λ i ( Wηi − z i ) 3 (12) Nh− vËy hÖ ph−¬ng tr×nh x©y dùng ®−îc cã thÓ coi lµ hÖ ph−¬ng tr×nh vi ph©n tæng qu¸t m« t¶ dao ®éng uèn cña kÕt cÊu nhÞp cÇu d©y v¨ng chÞu t¸c dông cña ®oµn t¶i träng «t« di ®éng. Ph¹m vi ¸p dông cho kÕt cÊu cÇu d©y v¨ng nhiÒu nhÞp, cã cÊu t¹o th¸p cÇu vµ s¬ ®å d©y ®a d¹ng, chÞu t¸c dông cña ®oµn t¶i träng «t« di ®éng cã khèi l−îng, vËn tèc vµ cù ly xe bÊt kú. Bµi to¸n dao ®éng ®µn håi tuyÕn tÝnh cã thÓ coi lµ mét tr−êng hîp ®Æc biÖt khi chän c¸c tham sè ¶nh h−ëng phi tuyÕn λ i = 0 vµ φ LH = 0 . i §Ó gi¶i hÖ ph−¬ng tr×nh vi ph©n hçn hîp gåm 1 ph−¬ng tr×nh vi ph©n ®¹o hµm riªng (9) vµ N ph−¬ng tr×nh vi ph©n th−êng (10) trªn cÇn ®−a hÖ vÒ hÖ ph−¬ng tr×nh vi ph©n th−êng. Sö dông ph−¬ng ph¸p Ritz suy réng, b»ng viÖc sö dông ph−¬ng ph¸p ®Æt biÕn phô t−¬ng tù nh− c¸c nghiªn cøu tr−íc ®©y [1] sÏ ®−a hÖ trë vÒ hÖ gåm (n + N) ph−¬ng tr×nh vi ph©n th−êng. BiÓu diÔn hÖ ph−¬ng tr×nh vi ph©n th−êng d−íi d¹ng ma trËn: {&&(t)} = [ B * (t) ]{q(t)} + [ C * (t)]{q(t)} + {f * (t)} & (13) q trong ®ã: [ B * (t)] vµ [ C * (t)] lµ c¸c ma trËn vu«ng, kÝch th−íc (n + N) x (n + N); { q(t) }, { q(t) }, { q(t) } vµ { f * (t) } lµ c¸c vÐct¬ cã (n + N) phÇn tö. && & C¸c ma trËn [ B (t)] vµ [ C(t)] cã d¹ng: ⎡ [ B (t) ] [ B q z (t) ] ⎤ ⎡ [ C ( t) ] [ C q z ( t) ] ⎤ [ ] ⎢ qq ⎥ ⎢ ⎥ qq [ C(t) ] = ⎢ * B (t) = ⎢ ⎥; ⎥ ⎢[ B (t) ] [ B z z ( t ) ]⎥ ⎢[ C (t) ] [ C z z ( t ) ]⎥ ⎢ zq ⎥ ⎢ zq ⎥ ⎣ ⎦ ⎣ ⎦ { f(t) } cã d¹ng: VÐc t¬ {f(t)} = {[fq (t)] [fz1 (t)] } Tuú theo møc ®é phøc t¹p cña m« h×nh bµi to¸n lùa chän mµ sÏ dÇn ®−a thªm c¸c yÕu tè phi tuyÕn vµo hÖ ph−¬ng tr×nh vi ph©n dao ®éng tæng qu¸t. Trong qu¸ tr×nh nghiªn cøu ®· thiÕt lËp thuËt to¸n víi ba m« h×nh cña hÖ dao ®éng: • M« h×nh dao ®éng cña hÖ ®µn håi tuyÕn tÝnh ( λi = 0 vµ φ LH = 0 ) i • M« h×nh dao ®éng phi tuyÕn cã xÐt ¶nh h−ëng cña ®é vâng cña c¸c d©y v¨ng, kh«ng xÐt t¸c ®éng phi tuyÕn cña ¸p lùc xe vµ yÕu tè l¾c ngang cña th¸p cÇu ( λi = 0 vµ φ LH ≠ 0 ). i
• M« h×nh dao ®éng phi tuyÕn xÐt ®ång thêi yÕu tè l¾c ngang cña th¸p cÇu vµ ¶nh h−ëng phi tuyÕn do t¸c ®éng cña t¶i träng vµ ®é vâng cña c¸c d©y v¨ng ( λ i ≠ 0 vµ φ LH ≠ 0 ). i Trong thuËt to¸n m« h×nh kh¸c nhau sÏ kh¸c nhau ë cÊu t¹o c¸c sè h¹ng trong c¸c ma trËn [ C (t) ] vµ vect¬ { f(t) }. ViÖc gi¶i hÖ ph−¬ng tr×nh vi ph©n d−íi d¹ng ma tr©n nªu trªn sÏ sö dông ph−¬ng ph¸p Runge-Kutta vµ thùc hiÖn trªn m¸y vi tÝnh PC. 3. ThuËt to¸n vμ phÇn mÒm ph©n tÝch dao ®éng cña hÖ Néi dung tÝnh to¸n trªn m¸y vi tÝnh (PC) ®−îc tiÕn hµnh theo tr×nh tù sau: • Chia thêi gian T ®Ó N t¶i träng qua dÇm thµnh c¸c b−íc thêi gian ti víi c¸c b−íc chia h ®ñ nhá. Sè b−íc thêi gian (btg) cÇn chän tõ 1 000 ®Õn 10000 b−íc tuú theo chiÒu dµi cÇu vµ sè t¶i träng. C¸c tham sè vÒ thêi gian cã quan hÖ: ⎧T − tæng thêi gian tÝnh to¸n ⎪ T h= ⎨ (14) ⎪btg - sè b−íc thêi gian (btg) ⎩ [ ][ ] { } • T¹i mçi b−íc thêi gian tÝnh ®−îc c¸c ma trËn B * (t) , C * (t) vµ vect¬ f * (t) . • Dïng ph−¬ng ph¸p Runge-Kutta ®Ó gi¶i hÖ ph−¬ng tr×nh vi ph©n d−íi d¹ng vect¬ : { && (t) } = [ B * (t) ]{ q (t) } + [ C * (t) ]{ q (t) } + { f * (t) } & q KÕt qu¶ t¹i mçi b−íc chia thêi gian tÝnh ®−îc c¸c q r ( t) víi (r = 1...n) . • Thay thÕ c¸c gi¸ trÞ q r ( t) vµo c¸c c«ng thøc t−¬ng øng tÝnh ®−îc c¸c gi¸ trÞ ®é vâng ®éng lùc vµ øng suÊt ®éng lùc ë vÞ trÝ bÊt kú ë thêi ®iÓm cÇn xÐt: rπ x n ∑ q r sin l W( x, t) = (15) r =1 EJ d ⎡ n 2 rπ x ⎤ 2 rπ x ⎛ rπ ⎞ n ⎢∑ r q r (t) sin + θ∑ ⎜ ⎟ q r (t) sin ⎥ σ( x, t) = (16) l r =1 ⎝ l ⎠ l⎥ l 2Mku ⎢ r =1 ⎣ ⎦ trong c«ng thøc (16): M ku = J d / y w - m«men kh¸ng uèn, cã gi¸ trÞ thay ®æi phô thuéc vµo m«men qu¸n tÝnh j chèng uèn vµ kho¶ng c¸ch tõ trôc trung hoµ cña dÇm tíi ®iÓm cÇn xÐt øng suÊt ®éng. ThuËt to¸n ®· lËp trªn ®©y lµ c¬ së cho viÖc x©y dùng c¸c phÇn mÒm tÝnh to¸n cã tªn VICABLE-1 ®Ó kh¶o s¸t dao ®éng ®µn håi tuyÕn tÝnh vµ phÇn mÒm VINOLINE-2 dïng ®Ó ph©n tÝch dao ®éng uèn phi tuyÕn cña kÕt cÊu nhÞp cÇu d©y v¨ng chÞu t¸c dông cña nhiÒu t¶i träng di ®éng. S¬ ®å khèi cña c¸c ch−¬ng tr×nh tÝnh to¸n thÓ hiÖn trªn h×nh 7.
NhËp sè liÖu t := 0; q i ( 0 ) = q i 0 ; q i ( 0 ) = q i 0 ; i = 1 ... n ; TÝnh : q n +1 ( 0 ) = z 0 ; q n +1 ( 0 ) = z 0 & & t = t+h r TÝnh c¸c ma trËn : B * ( t ); C * ( t ); f * ( t ) r r r r Gi¶i ph−¬ng tr×nh: q& = B * ( t )q + C * ( t )q + f * ( t ) & & t≥T §óng TÝnh øng suÊt ®éng σ (x,t) vµ ®é vâng ®éng W(x,t) In kÕt qu¶ KÕt thóc H×nh 7. S¬ ®å khèi cña ch−¬ng tr×nh VICBLE-1 vμ VINONLINE-2. Møc ®é chÝnh x¸c cña viÖc gi¶i ph−¬ng tr×nh b»ng ph−¬ng ph¸p sè phô thuéc vµo lÊy sè sè h¹ng n cña to¹ ®é suy réng q(t) tøc lµ sè c¸c sè h¹ng sau chuçi nghiÖm cña ph−¬ng tr×nh vi ph©n. Mét khã kh¨n kh¸c cña viÖc gi¶i bµi to¸n trªn lµ chän c¸c h»ng sè phi tuyÕn λ i vµ φLH v× i theo tÝnh chÊt cña c¸c ph−¬ng tr×nh phi tuyÕn ¶nh h−ëng lín ®Õn kh¶ n¨ng t×m nghiÖm chung cña hÖ. Trong c¸c kÕt qu¶ tÝnh to¸n thö nghiÖm ®· chän c¸c trÞ sè nµy trong kho¶ng tõ 0.5 ®Õn 0.9 λ i vµ φLH . i ViÖc x©y dùng c¸c phÇn mÒm tÝnh to¸n chØ thuËn lîi ®èi víi c¸c m« h×nh 1 vµ 2. Bµi to¸n dao ®éng uèn phi tuyÕn cña cÇu d©y v¨ng cã m« h×nh tæng qu¸t cã xÐt c¶ c¸c yÕu tè phi tuyÕn cña t¶i träng, ®é vâng d©y v¨ng vµ yÕu tè l¾c ngang cña trô cæng th−êng gÆp khã kh¨n ë c«ng cô tÝnh to¸n do khèi l−îng tÝnh to¸n qu¸ lín.
IV. Kh¶o s¸t ¶nh h−ëng cña yÕu tè phi tuyÕn do ®é vâng cña c¸c d©y ®Õn tr¹ng th¸i dao ®éng cña cÇu d©y v¨ng Sö dông ch−¬ng tr×nh VINONLINE-2, vµ ch−¬ng tr×nh VICABLE-1 ®Ó kh¶o s¸t tr¹ng th¸i dao ®éng cña mét sè c«ng tr×nh cÇu d©y v¨ng thùc tÕ t−¬ng øng víi c¸c m« h×nh bµi to¸n dao ®éng ®µn håi tuyÕn tÝnh vµ dao ®éng phi tuyÕn. Trong b¶ng 1 lµ kÕt qu¶ so s¸nh møc ®é kh¸c biÖt cña c¸c trÞ sè ®é vâng vµ øng suÊt ®éng lùc khi tÝnh theo 2 thuËt to¸n víi c¸c gi¶ thiÕt c¸c gèi d−íi c¸c d©y v¨ng lµ ®µn håi tuyÕn tÝnh vµ cã xÐt c¸c yÕu tè phi tuyÕn cho mét cÇu d©y v¨ng 3 nhÞp (cÇu §akr«ng). KÕt qu¶ cho thÊy khi sè l−îng t¶i träng t¨ng lªn th× møc ®é sai lÖch cña kÕt qu¶ tÝnh to¸n theo hai m« h×nh t¨ng ë møc ®é ®¸ng kÓ. B¶ng 1 KÕt qu¶ tÝnh to¸n ®é vâng ®éng lùc KÕt qu¶ tÝnh to¸n øng suÊt ®éng lùc Sè Khèi VËn tèc l−îng l−îng (103 KN/m2) (Km/h) (mm) t¶i t¶i Sai Sai träng träng VICABLE-1 VINONLINE.2 VICABLE-1 VINONLINE.2 lÖch % lÖch % -m/c (T) 1 1 30 13.3 4.997 5.869 14.86 11.970 14.427 17.03 3 16.407 20.953 21.69 13.986 15.705 10.95 2 1 30 13.3 5.107 5.869 12.98 12.150 14.427 15.78 3 20.065 26.364 23.89 13.419 17.266 22.28 6 1 30 5.107 - - 12.1498 14.299 15.03 3 20.177 27.989 24.33 14.900 10.816 -37.75 Trªn h×nh 8 giíi thiÖu biÓu ®å ®é vâng vµ øng suÊt ®éng lùc t¹i mÆt c¾t gi÷a nhÞp biªn vµ gi÷a nhÞp chÝnh cña cÇu §akr«ng do t¸c dông cña nhiÒu t¶i träng tÝnh theo 2 ch−¬ng tr×nh VICABLE-1 vµ VINONLINE-2. 103KN/m2 mm MÆt c¾t 3 MÆt c¾t 3 40 18.00 1b-tinh theo vICABLE-1 1b-tinh theo vICABLE-1 2b-tÝnh theo VINONLINE-2 2b-tÝnh theo VINONLINE-2 2b §é vâng ®éng øng suÊt ®éng 30 16.00 1b 1b 2a 20 14.00 MÆt c¾t 1 1a-tinh theo vICABLE-1 2a-tÝnh theo VINONLINE-2 2b MÆt c¾t 1 1a-tinh theo vICABLE-1 2a-tÝnh theo VINONLINE-2 2a 5 1a 12.00 1a 1 1 2 3 4 5 6 xe 2 3 4 5 6 xe H×nh 8. BiÓu ®å ®é vâng vμ øng suÊt ®éng lùc t¹i mÆt c¾t gi÷a nhÞp biªn vμ gi÷a nhÞp chÝnh cña cÇu §akr«ng.
KÕt qu¶ so s¸nh trong b¶ng1 vµ h×nh 8 ®· cho thÊy ¶nh huëng ®¸ng kÓ cña yÕu tè phi tuyÕn cña gèi ®ì ®µn håi víi tr¹ng th¸i øng suÊt vµ biÕn d¹ng cña dÇm cøng trong cÇu d©y v¨ng. Khi xÐt ®Õn tham sè phi tuyÕn ®é vâng cã xu thÕ t¨ng thªm trong khi trÞ sè øng suÊt l¹i cã xu thÕ gi¶m ®i. KÕt qu¶ nghiªn cøu phï hîp víi kÕt qu¶ nghiªn cøu cña mét sè t¸c gi¶ n−íc ngoµi [3], [4], [5]. Møc ®é sai lÖch lín nhÊt 24,33% víi c¸c trÞ sè ®é vâng vµ 37,75% ®èi víi trÞ sè øng suÊt. §é sai lÖch cã xu h−íng t¨ng lªn khi cã nhiÒu t¶i träng ®ång thêi di ®éng trªn cÇu vµ vËn tèc t¶i träng cao. σ-103KN/m2 25(30) [w -mm] 1. §é vâng ®éng lùc 23(28) 1.a- TheoVICABLE-1; 1b - Theo VINONLINE-2 21(26) 19(24) 17(22) 15(20) 13(18) 11(16) 2. øng suÊt ®éng lùc 2.a- TheoVICABLE-1; 2b - Theo VINONLINE-2 09(14) 1.8 10 20 30 40 50 60 70 80 90 100 120 140 v (km/h) H×nh 9. BiÕn thiªn ®é vâng vμ øng suÊt ®éng lùc theo vËn tèc t¶i träng. (1+μ) 2.1 1. HÖ sè ®éng lùc cña dé vâng 1.9 1.a- TheoVICABLE-1; 1b - Theo VINONLINE-2 1.7 1.5 1.3 1.1 2. HÖ sè ®éng lùc cña øng suÊt 0.9 2.a- TheoVICABLE-1; 2b - Theo VINONLINE-2 1.8 10 20 30 40 50 60 70 80 90 100 120 140 v (km/h) H×nh 10. BiÕn thiªn hÖ sè ®éng lùc cña ®é vâng vμ hÖ sè ®éng lùc cña øng suÊt ®éng lùc theo vËn tèc t¶i träng. Trªn h×nh 9 thÓ hiÖn sù biÕn thiªn ®é vâng, øng suÊt ®éng lùc theo sù biÕn ®æi cña c¸c vËn tèc t¶i träng qua cÇu tÝnh theo c¸c ch−¬ng tr×nh VICABLE-1 vµ VINONLINE-2 d−íi t¸c dông cña mét t¶i träng 13.3T di ®éng víi tèc ®é 80 km/h. KÕt qu¶ cho thÊy khi xÐt ®Õn yÕu tè phi tuyÕn cña c¸c gèi ®µn håi ®é vâng ®éng lùc t¨ng lªn ®¸ng kÓ. TrÞ sè chªnh lÖch lín nhÊt lµ 23.31%, t−¬ng øng víi tr−êng hîp vËn tèc t¶i träng b»ng 20 km/h. Víi xu thÕ ng−îc l¹i c¸c trÞ sè øng suÊt ®éng lùc l¹i gi¶m ®i kh¸ lín. Møc ®é gi¶m trÞ sè ®éng lùc lín nhÊt lµ 37,78 %, t−¬ng øng víi t¶i träng qua cÇu víi vËn tèc 140 Km/h. C¸c kÕt qu¶ nghiªn cøu ®−îc so s¸nh víi kÕt qu¶ thùc nghiÖm cña cïng h−íng nghiªn cøu tr−íc ®©y ®Ó kÕt luËn vÒ ®é tin cËy cña thuËt to¸n vµ ch−¬ng tr×nh ®· lËp [5] (b¶ng 2).
B¶ng 2 §èi chiÕu trÞ sè ®é vâng ®éng lùc lín nhÊt d−íi t¸c dông cña t¶i träng di ®éng T¶i träng TrÞ sè §é vâng ®éng lùc lín nhÊt (mm) Khèi VËn MÆt c¾t LÇn Sai lÖch Sai lÖch Thùc Lý thuyÕt theo Lý thuyÕt theo l−îng tèc thö nghiÖm VICABLE-1 VINONLINE-2 % % (kg) (km/h) I-I 3.5 3.449 -1.40 3.92 10.71 1 13030 10 III -III 15.88 12.33 -22.35 15.395 -3.15 IV-IV 9.83 9.71 -1.22 12.342 10.92 I-I 4.00 3.95 1.26 3.95 -1.26 6 13030 25 III-III 13.28 12.33 -7. 70 15.65 15.14 IV-IV 11.88 9.79 -17. 59 12.432 4. 44 8 13030 23 III-III 17.80 15.657 -13.68 19.57 8.72 V. KÕt luËn 1. KÕt qu¶ nghiªn cøu ®· cho thÊy sù kh¸c biÖt ®¸ng kÓ do ¶nh h−ëng cña c¸c yÕu tè phi tuyÕn ®Õn c¸c hiÖu øng ®éng lùc trong cÇu d©y v¨ng d−íi t¸c dông cña ®oµn t¶i träng di ®éng. §èi víi c¸c vïng vËn tèc nhá (v = 10 - 60 km/h) ¶nh h−ëng nµy ch−a lín (kho¶ng 5 - 7%). Tuy nhiªn víi c¸c vïng vËn tèc cao (v = 80 - 100 km/h) møc ®é sai lÖch lªn tíi (22 - 33%). 2. ViÖc tÝnh to¸n b»ng c¶ hai ch−¬ng tr×nh tÝnh kh«ng xÐt vµ cã xÐt ¶nh h−ëng phi tuyÕn ®Òu cho thÊy quy luËt biÕn thiªn phøc t¹p cña c¸c hiÖu øng ®éng lùc vµ hÖ sè ®éng lùc d−íi t¸c dông cña c¸c ®oµn t¶i träng di ®éng. KÕt qu¶ ph©n tÝch còng cho thÊy d−íi t¸c dông ®ång thêi cña nhiÒu t¶i träng di ®éng hiÖu øng ®éng lùc cã xu thÕ gi¶m ®i so víi tr−êng hîp chØ cã mét t¶i träng di ®éng. §iÒu nµy cho phÐp gi¶i thÝch c¸ch tÝnh hÖ sè ®éng lùc trong mét sè Quy tr×nh vµ Tiªu chuÈn thiÕt kÕ cÇu cña c¸c n−íc kh¸c nhau, cã thÓ trî gióp cho c«ng t¸c thiÕt kÕ c¸c c«ng tr×nh cÇu. 3. C¸c c«ng tr×nh cÇu d©y v¨ng cã tr¹ng th¸i dao ®éng phøc t¹p, ®ßi hái cÇn nghiªn cøu ngµy cµng ®Çy ®ñ vµ gÇn s¸t h¬n víi m« h×nh lµm viÖc thùc tÕ cña c«ng tr×nh, trong ®ã cÇn chó ý tíi c¸c yÕu tè phi tuyÕn. 4. Møc ®é khã kh¨n do ®ßi hái c«ng cô m¹nh ë kh©u tÝnh to¸n gÆp trong qu¸ tr×nh nghiªn cøu bµi to¸n dao ®éng phi tuyÕn ®· cho thÊy sù cÇn thiÕt cña viÖc x©y dùng c¸c m« h×nh phï hîp h¬n nh»m ®¬n gi¶n hãa bµi to¸n ®Ó cã thÓ ¸p dông thuËn tiÖn cho c«ng t¸c thiÕt kÕ c¸c c«ng tr×nh cÇu d©y v¨ng ë ViÖt nam. Tµi liÖu tham kh¶o [1]. Hoμng Hμ. Nghiªn cøu dao ®éng uèn cña kÕt cÊu nhÞp cÇu d©y v¨ng trªn ®−êng «t« chÞu t¸c dông cña ho¹t t¶i khai th¸c. LuËn ¸n TiÕn sü kü thuËt. §¹i häc GTVT, Hµ Néi, 1999.
[2]. Hoμng Hμ. Nghiªn cøu dao ®éng uèn phi tuyÕn cña kÕt cÊu nhÞp cÇu d©y v¨ng chÞu t¸c dông cña ®oµn t¶i träng di ®éng. B¸o c¸o ®Ò tµi nghiªn cøu khoa häc cÊp Bé, M· sè B99-35-75. Hµ Néi, 2002. [3]. Fuheng Yang and Ghislain A. Fonder. Dynamic Response of Cable-Stayed Bridger under Moving Loads. J. of Engineering Mechanics, July, 1998. [4]. Anil K. Chopra. Dynamics of Structures. University of California at Berkeley. Prentice Hall. USA, 1995. [5]. Chen D.W. and Xiang H.F. Practical method of second order theory of Cable-Stayed Bridges in China. J. of Urban Road and Flood Cantrol, 1-12, 1988