ThiÕt kÕ bé ®iÒu khiÓn ph¶n håi ®Çu ra cho cÇu trôc
KS. trÞnh l−¬ng miªn
Bé m«n §iÒu khiÓn häc
Khoa §iÖn - §iÖn tö
Tr−êng §¹i häc Giao th«ng VËn t¶i
Tãm t¾t: Bμi b¸o ®−a ra m« h×nh to¸n cña hÖ cÇu trôc vμ kÕt qu¶ thiÕt kÕ bé ®iÒu khiÓn
ph¶n håi tr¹ng th¸i khi thªm thμnh phÇn tÝch ph©n nh»m tù ®éng ho¸ cÇu trôc ®¶m b¶o triÖt tiªu
sai lÖch tÜnh: vÞ trÝ xe vμ dao ®éng t¶i.
Summary: This paper puts forwards mathematical models of the bridge crane and results
of the state feedback controller with an additional integrator to operate the bridge crane
automatically, ensuring minimized position errors and swing of loads.
I. §Æt vÊn ®Ò
CÇu trôc lµ thiÕt bÞ c«ng nghiÖp ®−îc øng dông rÊt réng r·i trong nhiÒu lÜnh vùc nh− trong
x©y dùng, trong nhµ m¸y hay t¹i c¸c bÕn c¶ng, ... Nh÷ng cÇu trôc nµy th−êng ®iÒu khiÓn b»ng
tay. Khi mµ kÝch th−íc cña cÇu trôc trë nªn lín h¬n vµ yªu cÇu vËn chuyÓn nhanh h¬n th× qu¸
tr×nh ®iÒu khiÓn chóng sÏ trë nªn khã kh¨n nÕu kh«ng ®−îc tù ®éng ho¸. CÇu trôc di chuyÓn
theo nh÷ng quü ®¹o x¸c ®Þnh. Nh−ng nã ho¹t ®éng d−íi nh÷ng ®iÒu kiÖn hÕt søc kh¾c nghiÖt vµ
mét hÖ thèng ®iÒu khiÓn kÝn lµ thÝch hîp nhÊt.
CT 2
CÇu trôc lµ hÖ rÊt phøc t¹p. Trong suèt thêi gian qua ®· cã kh¸ nhiÒu c¸c nghiªn cøu [1-5]
vÒ cÇu trôc nh»m t×m ra ph−¬ng ph¸p vËn hµnh nã mét c¸ch hiÖu qu¶. Trong sè c¸c nghiªn cøu
®ã th× ph−¬ng ph¸p ®iÒu khiÓn cÇu trôc dùa vµo m« h×nh tuyÕn tÝnh ®· thu ®−îc mét vµi kÕt qu¶
kh¶ quan [6-7]. Tuy nhiªn, vÊn ®Ò tån t¹i lµ c¸c bé ®iÒu khiÓn ®−îc thiÕt kÕ ch−a triÖt tiªu ®−îc
sai lÖch tÜnh. Do vËy, b»ng c¸ch ®−a thªm kh©u tÝch ph©n vµo bé ®iÒu khiÓn ph¶n håi tr¹ng th¸i
sÏ ®¶m b¶o sai lÖch tÜnh cña hÖ thèng ®−îc triÖt tiªu hoµn toµn vµ chÊt l−îng ®iÒu khiÓn ®−îc
n©ng cao.
ii. M« h×nh to¸n hÖ cÇu trôc
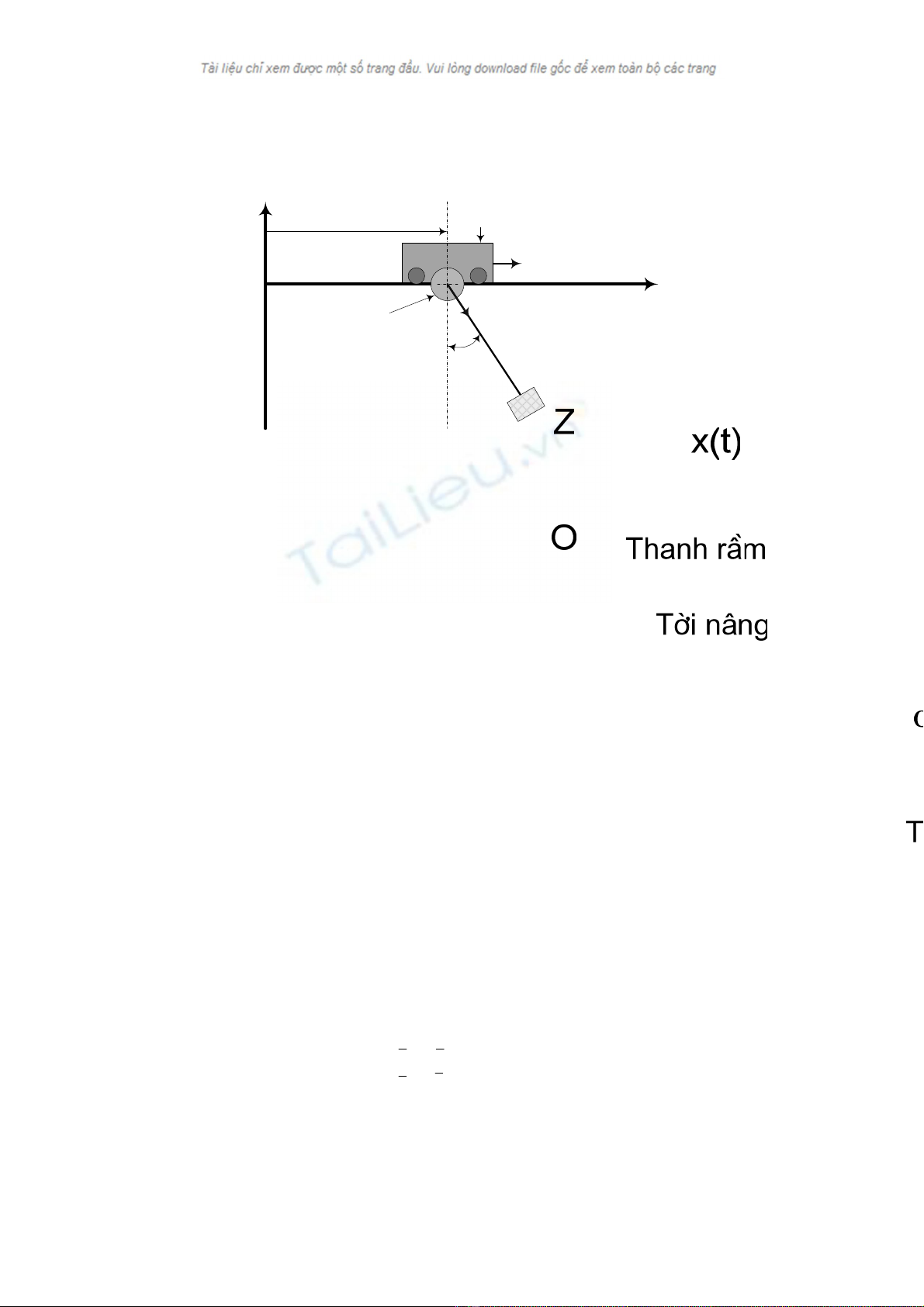
M« h×nh cÇu trôc víi hÖ to¹ ®é ®−îc chän nh− m« t¶ trªn h×nh 1. Trôc Ox n»m ngang däc
theo thanh dÇm, trôc Oz th¼ng ®øng cã chiÒu h−íng lªn trªn. Xe goßng di chuyÓn trªn thanh
dÇm víi vÞ trÝ ®−îc x¸c ®Þnh bëi x(t) lµ kho¶ng c¸ch ®o ®−îc tõ gèc O ®Õn ®iÓm treo cña c¸p
n©ng t¶i trªn xe. Coi t¶i nh− mét chÊt ®iÓm cã khèi l−îng mP, xe goßng cã khèi l−îng mt. T¶i
träng vµ xe goßng ®−îc nèi víi nhau b»ng mét c¸p cøng cã khèi l−îng kh«ng ®¸ng kÓ vµ cã
chiÒu dµi l, sù dµi ra cña d©y c¸p lµ kh«ng ®¸ng kÓ. Trong khi n©ng h¹ t¶i hay di chuyÓn xe th×
t¶i dao ®éng trong mÆt ph¼ng th¼ng ®øng víi gãc lÖch α(t). Fx lµ lùc chuyÓn ®éng xe goßng theo
h−íng x vµ Fl lµ lùc n©ng t¶i theo h−íng l.
CT 2
Thanh dÇm
H×nh 1. M« h×nh chuyÓn ®éng cÇu trôc trong hÖ to¹ ®é 2D
Ph−¬ng tr×nh chuyÓn ®éng cña hÖ cÇu trôc thu ®−îc tõ ph−¬ng tr×nh Lagrange vÒ c©n b»ng
n¨ng l−îng [1], [5], [9].
Sau khi tÝnh to¸n vµ biÕn ®æi, ta thu ®−îc ph−¬ng tr×nh ®éng lùc häc m« t¶ hÖ cÇu trôc nh−
sau [1]:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
α−α−=α+α
+α+α=+α
+αα+αα−=αα+α++
singllx)(cos
Fcosgmlmlmx)(sinm
F)(sinlml)(cosm)(coslml)(sinmx)mm(
lpppp
xpppppt
&
&
&&
&&
&
&&
&&
&&
&
&&
&&
&&
2
2
2
2
(2.1)
Theo (2.1) ta ®· x©y dùng ®−îc ph−¬ng tr×nh m« t¶ chuyÓn ®éng cÇu trôc tæng qu¸t khi
thùc hiÖn chuyÓn ®éng theo c¶ hai ph−¬ng x, l. Trong tr−êng hîp cè ®Þnh c¸p treo t¶i, l = h»ng
sè, ta cã , lóc nµy ph−¬ng tr×nh chuyÓn ®éng cña hÖ sÏ ®−îc viÕt l¹i nh− sau [9] 0== ll &&&
⎪
⎩
⎪
⎨
⎧
=α+α+α
=αα−αα++
0
2
singlcosx
F)sincos.(lmx)mm( xppt
&&
&&
&&&
&&
(2.2)
M« h×nh tuyÕn tÝnh dõng cña hÖ cÇu trôc thu ®−îc tõ gi¶ thiÕt gãc lÖch ®ñ nhá
1~cos,~sin ααα
⎩
⎨
⎧
−=α+α
=α++
xgl
Flmx)mm( xppt
&&
&&
&&
&& (2.3)
HÖ tuyÕn tÝnh (2.3) cã thÓ biÓu diÔn trong kh«ng gian tr¹ng th¸i nh− sau [5]
xCy
BuxAx
=
+=
&
(2.4)
víi
[]
T
xxx αα= &
&;
x
Fu =
;
g
lm
mm
m
gm
A
t
pt
t
p
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
+
−
=
000
1000
000
0010
;
m
m
B
p
t
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
=
1
0
1
0
⎥
⎦
⎤
⎢
⎣
⎡
=0100
0001
C (2.5)
Th«ng sè cÇu trôc ®−îc cho nh− sau:
- Khèi l−îng xe: mt = 2[kg]
- T¶i träng ban ®Çu: mp = 0.2[kg]
- ChiÒu dµi c¸p n©ng t¶i: 1[m]
- Kho¶ng c¸ch di chuyÓn xe: 0.2-1[m]
- Gãc l¾c dao ®éng lín nhÊt: α = 10O ~ 0.2 rad.
Iii. ThiÕt kÕ bé ®iÒu khiÓn
Theo nguyªn lý ®iÒu khiÓn ph¶n håi tr¹ng th¸i [7], bé ®iÒu khiÓn ®−îc chän cho hÖ (2.4) cã
d¹ng
xKFu x
−
=
=
(3.1)
víi
[
]
αα
=dpdxpx KKKKK ; Ki lµ c¸c h»ng sè
CT 2
Ta thÊy, luËt ®iÒu khiÓn ph¶n håi tr¹ng th¸i (3.1) dùa trªn nguyªn lý tû lÖ nªn sÏ tån t¹i sai
lÖch tÜnh. V× thùc chÊt, luËt (3.1) ®−îc tæng hîp theo m« h×nh tuyÕn tÝnh t−¬ng ®èi (2.4), (2.5). Do
vËy ®Ó triÖt tiªu sai lÖch tÜnh, chóng ta sÏ thªm mét kh©u tÝch ph©n vµo vßng ph¶n håi vÞ trÝ cña
xe goßng, tøc lµ mét biÕn xi ®−îc ®−a thªm vµo hÖ thèng nh− sau:
a
a
a
a
a
a
xCy
uBxAx
=
+=
&
(3.2)
víi
[]
T
ia xxxx αα= &
&
;
g
lm
mm
m
gm
A
t
pt
t
p
a
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
+
−
=
0000
10000
0000
00100
00010
;
m
m
B
p
t
a
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
=
1
0
1
0
0
⎥
⎦
⎤
⎢
⎣
⎡
=01000
00010
a
C (3.3)
LuËt ®iÒu khiÓn ph¶n håi tr¹ng th¸i khi nµy cã d¹ng:
a
ax xKFu
−
=
=
(3.4)
víi
[
]
αα
=dpdxpxixa KKKKKK .
Víi bé ®iÒu khiÓn (3.4) hÖ kÝn më réng (3.3), (3.4) sÏ nh− sau
a
aaaa
a
a
ax)KBA(uBxAx
−
=
+
=
& (3.5)
Nh− vËy, nÕu cho tr−íc c¸c ®iÓm cùc cña hÖ kÝn më réng lµ βi (i=1,5) th× c¸c hÖ sè cña bé
®iÒu khiÓn ph¶n håi tr¹ng th¸i Ka sÏ ®−îc x¸c ®Þnh tõ viÖc so s¸nh nghiÖm cña det(sI – (Aa-
BBaKa)) = 0 víi βi
0
1000
0010
0001
2345 =++
+
+
−++
+
−
+=
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−+
−
−
−−
+−
+
−
−
=−−
α
α
α
α
α
α
α
lm
gK
s
lm
gK
s
lm
KlK
s
lm
KlKg)mm(
s
lm
KlK
s
lm
K
s
lm
Kg)mm(
lm
K
lm
K
lm
Ks
m
K
m
Kgm
m
K
s
m
K
m
Ks
s
det))KBA(sIdet(
t
ix
t
px
t
dxix
t
ppxpt
t
ddx
t
d
t
ppt
t
d
t
px
t
ix
t
d
t
pp
t
dx
t
px
t
ix
aaa
Tõ ®©y, ta tÝnh ®−îc c¸c hÖ sè cña bé ®iÒu khiÓn ph¶n håi tr¹ng th¸i nh− sau:
g/)lm(K tix 54321 βββ
β
β=
g/)](lm[K tpx 54325431542153214321
β
β
β
β
+
β
β
β
β
+
β
β
β
β
+
β
βββ+ββ
β
β=
g/)]
(lmlK[K tixdx
543542532432
541531431521421321
βββ+βββ+βββ+βββ+
βββ+βββ+βββ+βββ+βββ+βββ+−= (3.6) CT 2
)
(lmg)mm(lKK tptpxp
54534352
423251413121
ββ+ββ+ββ+ββ+
ββ+ββ+ββ+ββ+ββ+ββ−++=
α
)(lmlKK tdxd 54321
β
+
β
+
β+β+β
−
=
α
D−íi ®©y lµ s¬ ®å cÊu tróc hÖ thèng ®iÒu khiÓn cÇu trôc dùa trªn nguyªn lý ph¶n håi tr¹ng
th¸i. Bé ®iÒu khiÓn ph¶n håi tr¹ng th¸i nµy ®−îc ®−a thªm vµo thµnh phÇn tÝch ph©n nh»m triÖt
tiªu sai lÖch tÜnh vÞ trÝ.
x
a
xd
0
x.ref f(u)
g_2
f(u)
g_1
f(u)
f2
f(u)
f1
0
a_ref
0
a.ref
1
s
1
s
1
s
1
s
1
s
Kpa
Kdx
Kpx
Kda
Kix
H×nh 2. Bé ®iÒu khiÓn ph¶n håi tr¹ng th¸i hÖ cÇu trôc
Víi th«ng sè cña cÇu trôc nh− trªn, tõ (3.6) ta tÝnh ®−îc c¸c hÖ sè khuÕch ®¹i cña bé ®iÒu
khiÓn ph¶n håi tr¹ng th¸i nh− sau:
[Kix Kpx Kdx Kpa Kda]T = [0.0100 1.5003 2.3833 -3.0465 -4.6255]T
S¬ ®å m« pháng hÖ thèng ®iÒu khiÓn cÇu trôc ®−îc x©y dùng trªn Matlab/Simulink nh− sau
xd
x
a
xd
x
x.
a
a.
Fx
PHTT
u=Fx
x
x.
a
a.
CraneXA
CT 2
H×nh 3. S¬ ®å m« pháng hÖ thèng ®iÒu khiÓn cÇu trôc trªn Matlab
IV. KÕt qu¶ m« pháng
Tr−êng hîp 1: Khi xe di chuyÓn ®Õn vÞ trÝ ®Æt 1.0m