CHƯƠNG 3
MÔ TẢTOÁN HỌC
MÔ
TẢ
TOÁN
HỌC
HỆ THỐNG ĐIỀU KHIỂN RỜI RẠC
31Hà t ề đ t
3
.
1
Hà
m
t
ru
yề
n
đ
ạ
t
3.2 Phương trình trạng thái
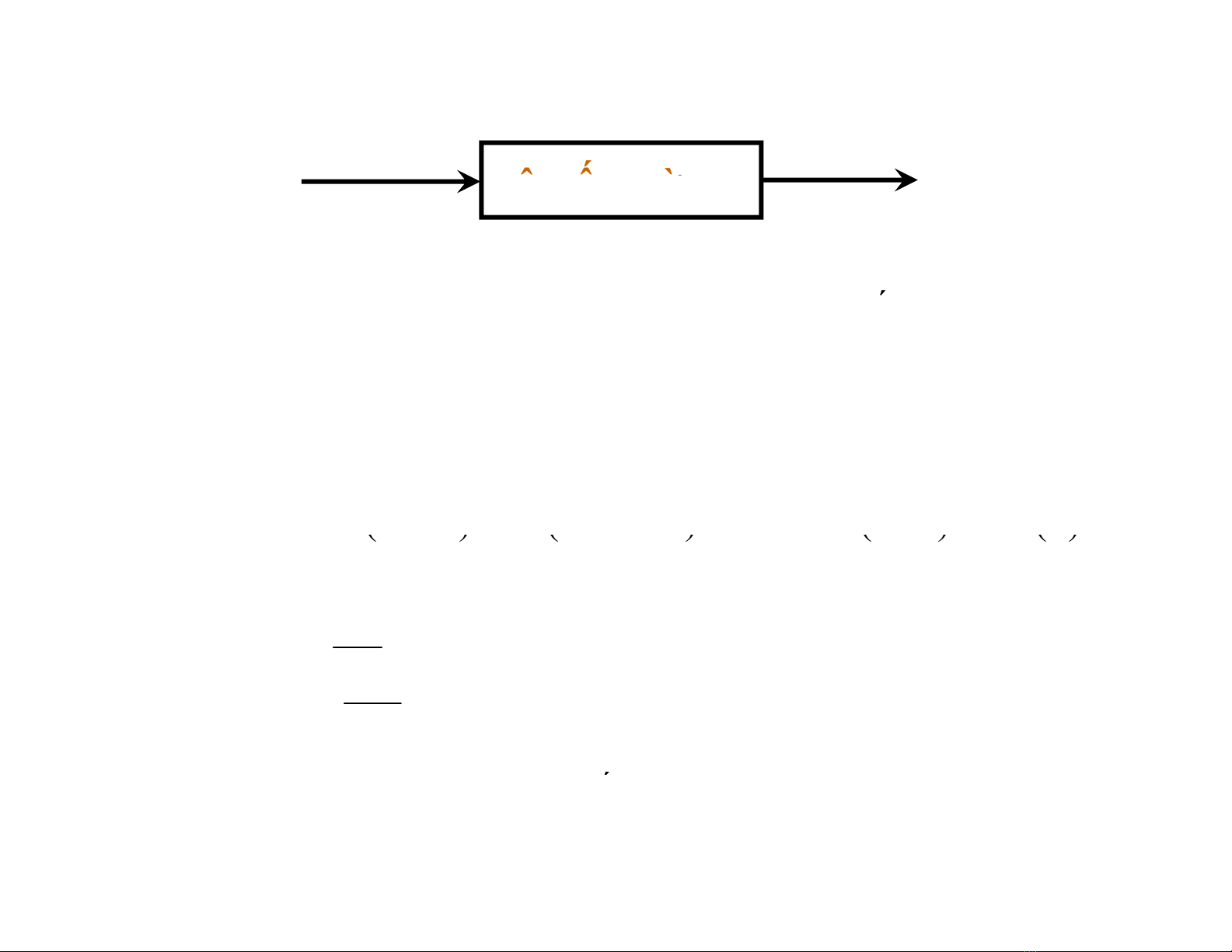
Hệthố ời
r(k) c(k)
3.1 HÀM TRUYỀN ĐẠT
ố
Hệ
thố
ng r
ời
rạc
tín hiệu vào tín hiệu ra
Quan hệ giữa tín hiệu vào và tín hiệu ra của hệ th
ố
ng rời rạc được
mô tả bằng phương trình sai phân:
)
(
)
1
(
...
)
1
(
)
(
)()1(...)1()(
1
1
0
110
k
rb
k
rbm
k
rbm
k
rb
kcakcankcankca
m
m
nn
+
+
+
+
−
+
+
+
=
+
+
+
+
−
+
++ −
)
(
)
(
)
(
)
(
1
1
0
m
m
−
(
)
⎪
⎧
Trong đó
(
)
()
:
0 ),0(
0 ),0(
0
0
⎪
⎩
⎪
⎨
⎧
≠=
≠
=
bmjb
ania
j
ithông sốcủa hệ thống
ố
n
≥
m, n: bậccủa hệ th
ố
n
g

[
]
[
]
)
(
...
)
(
...
1
1
1
0
1
1
1
0
z
R
b
z
b
z
b
z
b
z
C
a
z
a
z
a
z
a
mmnn
+
+
+
+
=
+
+
+
+
−−
Thực hiện biến đổi Z hai vế phương trình sai phân ta được:
[
]
[
]
)
(
...
)
(
...
1
1
0
1
1
0
z
R
b
z
b
z
b
z
b
z
C
a
z
a
z
a
z
a
mmnn
+
+
+
+
+
+
+
+
−
−
hàm tru
yề
n
Đặt
m
m
mm
b
z
b
z
b
z
b
z
C
G
+
+
+
+
−
1
1
1
0
...
)
(
)
(
y
hệ thống rời rạc
Đặt
nn
nn
m
m
azazaza
b
b
b
b
zR
z
C
z
G
++++
==
−
−
−
1
1
10
1
1
0
...
...
)(
)
(
)
(
Biến đổi tương đương G(z) về dạng:
()
⎟
⎟
⎞
⎜
⎜
⎛++++
==
−+−
−
−
−− m
m
m
m
mn zbzbzbb
z
zC
z
G
1
1
1
1
1
10 ...
)(
)
(
Hai cách bi
ể
u diễn trên tươn
g
đươn
g
nhau.
⎟
⎟
⎠
⎜
⎜
⎝
+
+
+
+
−
+
−
−
−
n
n
n
n
z
a
z
a
z
aa
z
R
G
1
1
1
10 ...)(
)
(
g g
Dạng thứ hai được sử dụng nhiều hơn.
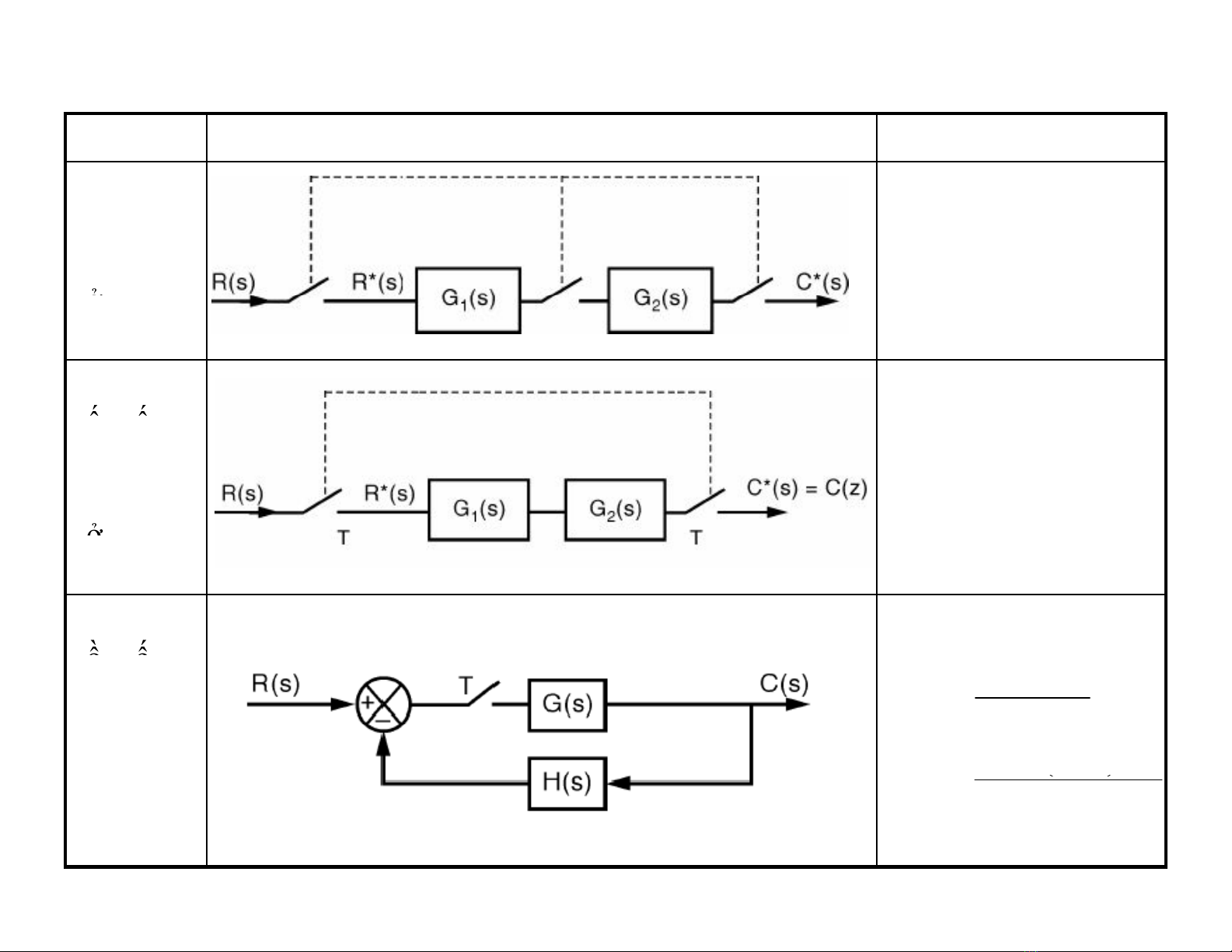
Tính hàm truyền hệ thống rời rạc từ sơ đồ khối
Hệ thống Hình Hàm truyền
Hai khâu
nối tiếp
cách nhau
bởi khâ
{}
{
}
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
=
=
)
(
)
(
)()(
)()()(
11
21
s
G
z
G
sGzG
zGzGzG
Z
Z
bởi
khâ
u
lấy mẫu
Hai khâu
ốitiế
{
}
⎠
⎝
=
)
(
)
(
22
s
G
z
G
Z
n
ối
tiế
p
không
cách nhau
bởi khâu
{}
)()(
)()(
21
21
sGsG
zGGzG
Z=
=
bởi
khâu
lấy mẫu
Hệ thống
hồitiếp
hồi
tiếp
có khâu
lấy mẫu
trong
{
}
)
(
)(1
)(
)(
sG
zGH
zG
zGk
Z
+
=
trong
kênh sai
số
{
}
{
}
)()(1
)
(
sHsGZ+
=
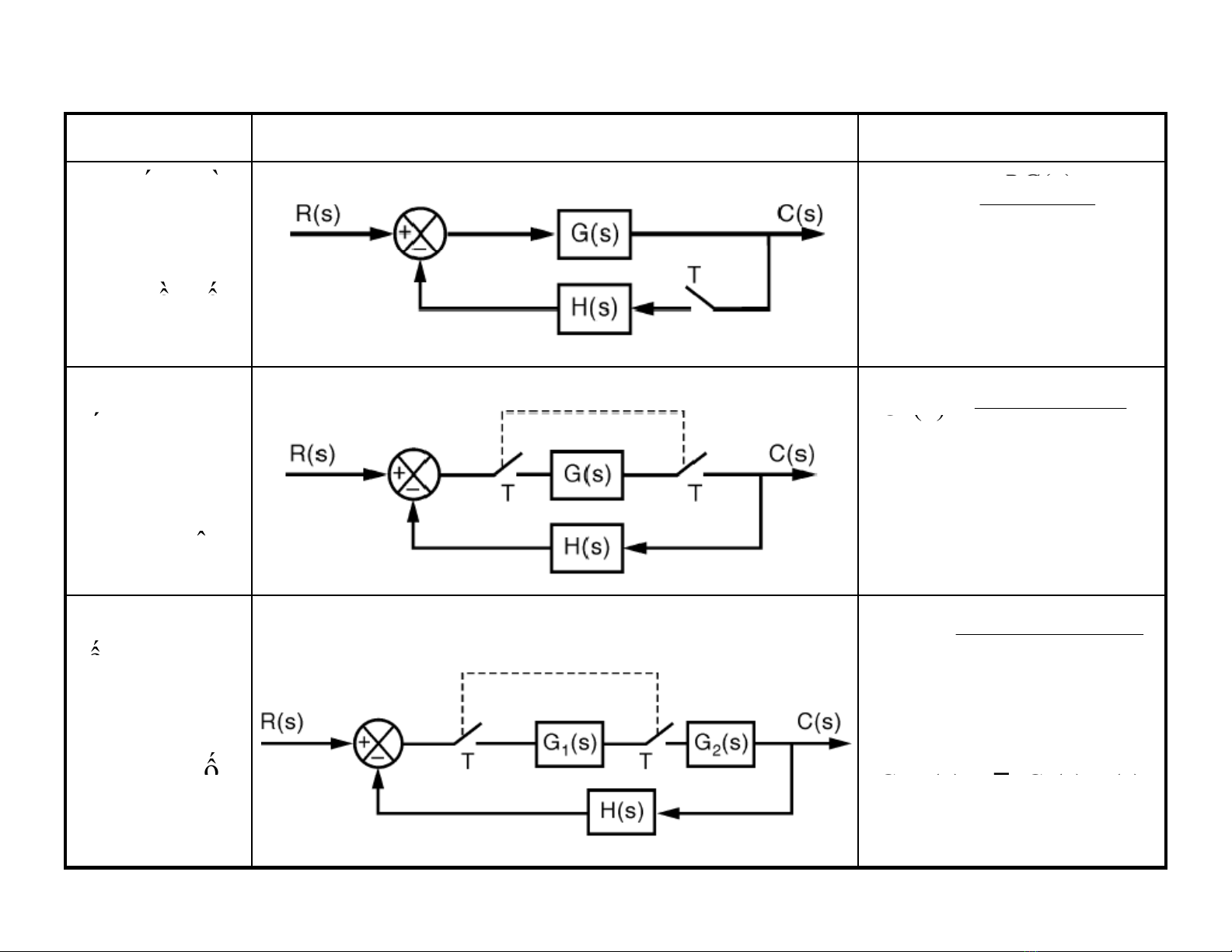
Tính hàm truyền hệ thống rời rạc từ sơ đồ khối
Hệ thống Hình Hàm truyền
ố ồ
)
(
RG
Hệ th
ố
ng h
ồ
i
tiếp có khâu
lấy mẫu trong
òng hồitiếp
{}
{
}
⎟
⎟
⎞
⎜
⎜
⎛=
+
=
)()()(
)(1
)
(
)(
sGsRzRG
zGH
z
RG
zC
Z
v
òng
hồi
tiếp
Hai khâu hồi
ế
{
}
⎟
⎟
⎠
⎜
⎜
⎝
=
)()()( sHsGzGH Z
=
)(
)
(
zG
z
G
k
ti
ế
p có các
khâu lấy mẫu
đồng bộ trong
há h th ậ
{}
{}
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
=
+
)()(
)()(
)()(1
)
(
sHzH
sGzG
z
H
z
G
G
k
Z
Z
n
há
n
h
th
u
ậ
n
Hệ thống hồi
tiếp có các
+
=
)
(
)
(
1
)()(
)( 21
z
H
G
z
G
zGzG
zGk
tiếp
có
các
khâu lấy mẫu
đồng bộ và
các khâu nối
{}
{}
{
}
⎟
⎟
⎟
⎞
⎜
⎜
⎜
⎛
=
=
+
)
(
)
(
)
(
)()(
)()(
)
(
)
(
1
22
11
21
G
G
sGzG
sGzG
z
H
G
z
G
Z
Z
Z
các
khâu
nối
tiếp ở nhánh
thuận
{
}
⎟
⎠
⎜
⎝
=
)
(
)
(
)
(
22 s
H
s
G
z
H
G
Z












![Bài giảng Cảm biến và ứng dụng: Chương 1 - Các khái niệm và đặc trưng cơ bản [Chuẩn SEO]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251204/kimphuong1001/135x160/51101764832169.jpg)



