Đáp án – Nguyên lý thống kê
v1.0 161
ĐÁP ÁN
Bài 2
Bài tập 1
Sắp xếp số liệu theo thứ tự từ nhỏ đến lớn, xác định được Xmax = 145, Xmin = 50.
Với khoảng cách tổ bằng nhau và bằng 10, bảng tần số phân bố được xây dựng như sau:
Năng lượng tiêu dùng
(triệu BTU) Tần số (hộ) Tần suất (lần)
50 – 60 8 0,16
60 – 70 7 0,14
70 – 80 3 0,06
80 – 90 6 0,12
90 – 100 10 0,20
100 – 110 5 0,10
110 – 120 4 0,08
120 – 130 2 0,04
130 – 140 3 0,06
140 – 150 2 0,04
Tổng 50 1,00
Từ đó tính được tần suất theo công thức: i
i
i
f
df
(kết quả như ở bảng trên).
Bài tập 2
Sắp xếp số liệu theo thứ tự từ nhỏ đến lớn.
a) Tổ đầu tiên bắt đầu từ 6 – 8. Biết khoảng cách các tổ bằng nhau và bằng 2, dãy số phân phối
được xây dựng như sau:
Lượng sắt dung nạp trong 24 giờ (mg) Số người
6 – 8 1
8 – 10 1
10 – 12 7
12 – 14 9
14 – 16 9
16 – 18 9
18 – 20 8
20 – 22 1
Tổng 45
b) Biết hàm lượng sắt cho phép dung nạp hàng ngày của phụ nữ dưới 51 tuổi là không vượt quá
18mg. Vậy với mẫu ở trên, tỷ lệ phần trăm số phụ nữ đã dung nạp quá mức lượng sắt cho
phép (tức có x ≥ 18) là:
(8 + 1)/45 = 0,2 (tức 20%)
Đáp án – Nguyên lý thống kê
162 v1.0
Bài tập 3
Sắp xếp số liệu theo thứ tự từ nhỏ đến lớn ta có: Xmax = 100, Xmin = 34.
a) Với khoảng cách tổ bằng nhau và bằng 10, bảng tần số phân bố như sau:
Điểm Tần số (số sinh viên) Tần suất (lần) Tần số tích luỹ
30 – 40 2 0,10 2
40 – 50 0 0,00 2
50 – 60 0 0,00 2
60 – 70 3 0,15 5
70 – 80 3 0,15 8
80 – 90 8 0,40 16
90 – 100 4 0,20 20
Tổng 20 1,00
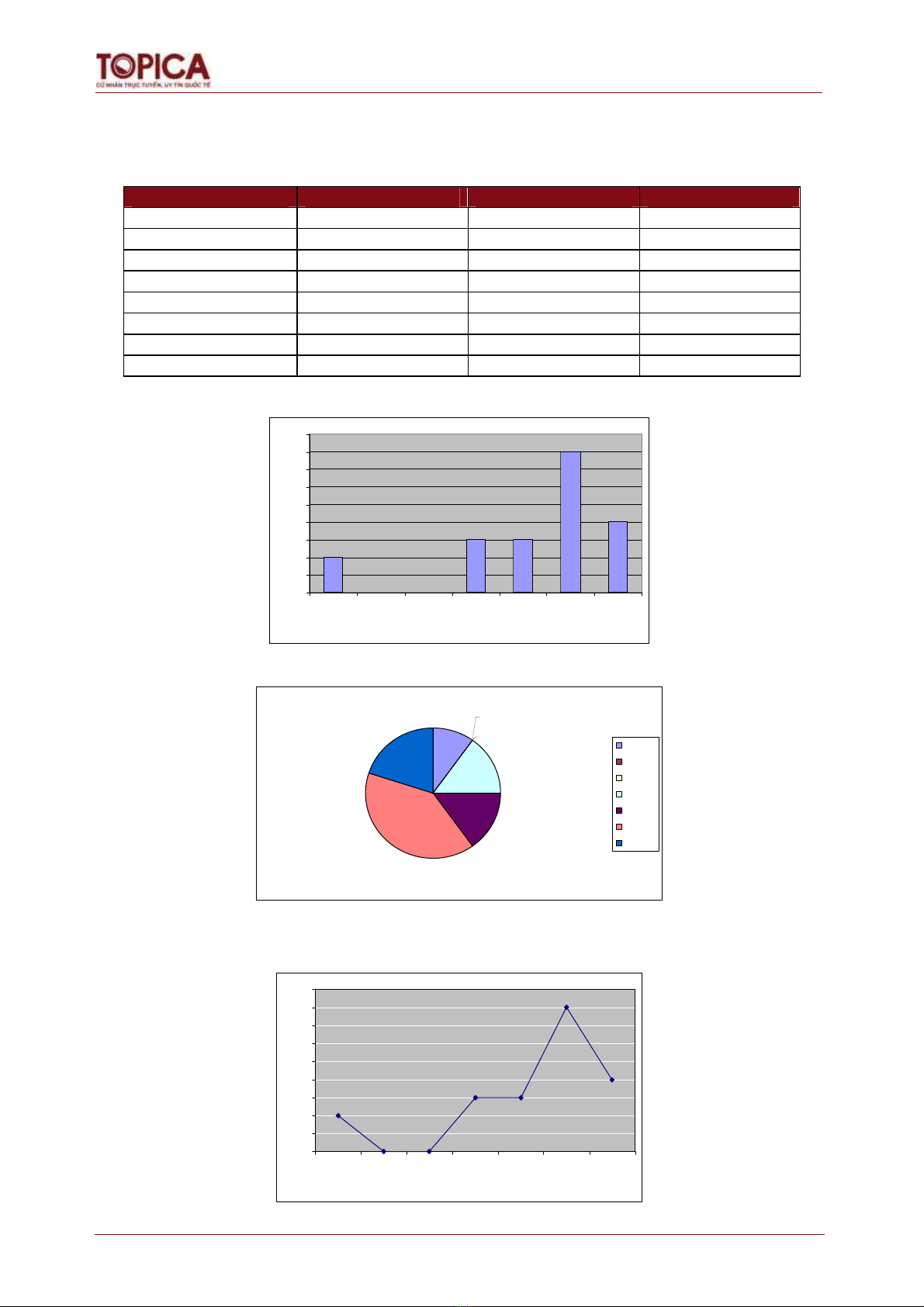
b) Biểu đồ tần số:
0
1
2
3
4
5
6
7
8
9
30-40 40-50 50-60 60-70 70-80 80-90 90-100
Điểm
Số sinh viên
Biểu đồ tần suất:
0.1 0
0
0.15
0.15
0.4
0.2
30-40
40-50
50-60
60-70
70-80
80-90
90-100
(Lưu ý: có thể sử dụng biểu đồ hình cột hoặc biểu đồ hình tròn đều được).
c) Đồ thị tần số
0
1
2
3
4
5
6
7
8
9
30-40 40-50 50-60 60-70 70-80 80-90 90-100
Điểm
Số sinh viên
Đáp án – Nguyên lý thống kê
v1.0 163
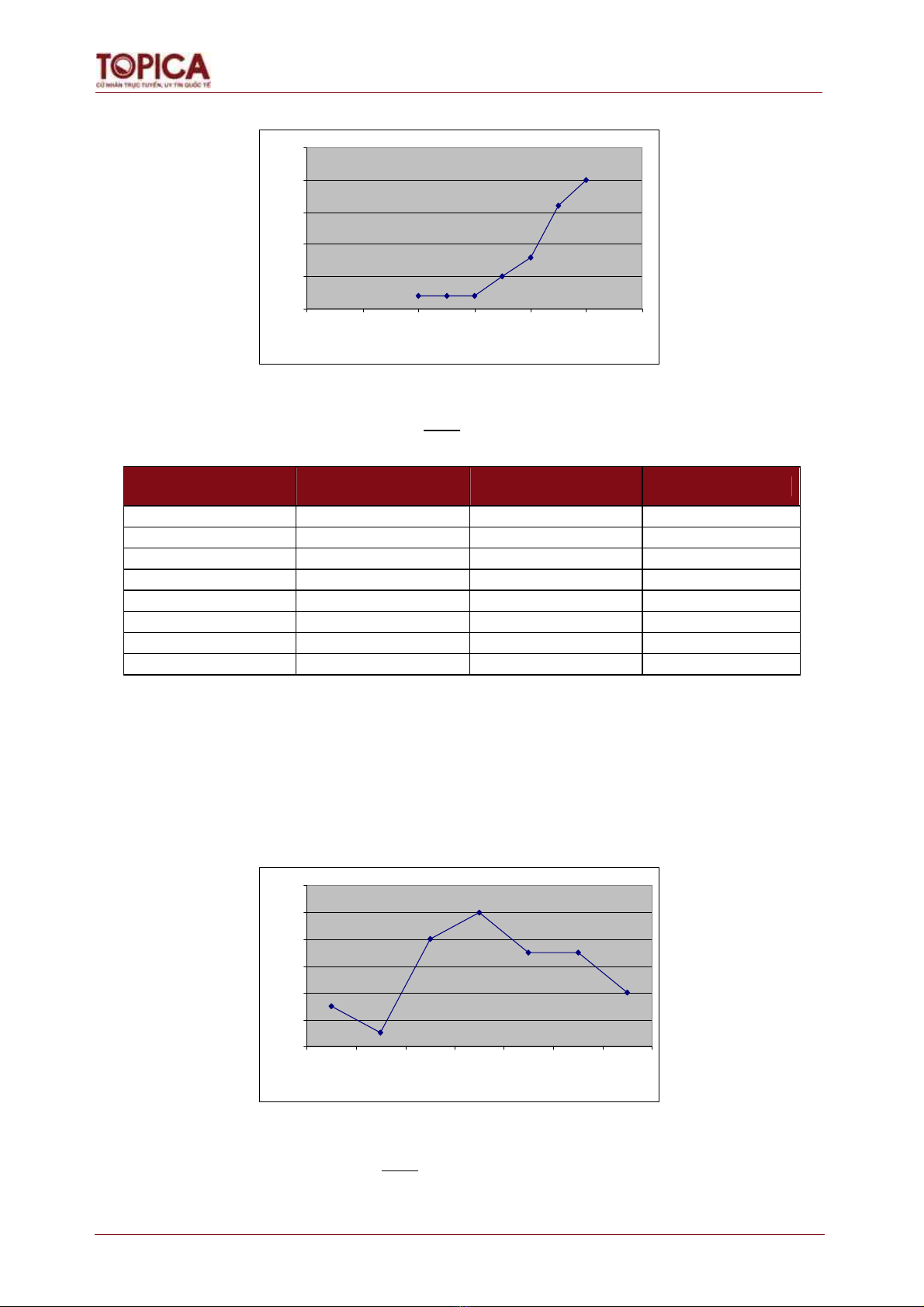
Đồ thị tần số tích luỹ
0
5
10
15
20
25
0 20406080100120
Điểm
Tần số tích luỹ
Bài tập 4
a) Tần suất được tính theo công thức: i
i
i
f
df
Số ngày đến hạn
thanh toán Số khoản đầu tư
ngắn hạn (f) Tần suất (lần) Tần số tích luỹ
30 – 40 3 0,075 3
40 – 50 1 0,025 4
50 – 60 8 0,200 12
60 – 70 10 0,250 22
70 – 80 7 0,175 29
80 – 90 7 0,175 36
90 – 100 4 0,100 40
Tổng 40
b) Để biết khoản đầu tư thứ 23 có số ngày đến hạn thanh toán là bao nhiêu, ta phải tính tần số
tích luỹ.
Nhìn vào bảng tần số tích lũy ở trên thì khoản đầu tư thứ 23 nằm ở tổ thứ 5 và do đó có số
ngày đến hạn thanh toán là 70 – 80 ngày.
c) Cũng theo bảng tần số tích lũy ở trên thì số khoản đầu tư có ngày đến hạn thanh toán dưới 70
ngày là 22 khoản.
d) Đồ thị biểu diễn mối liên hệ:
0
2
4
6
8
10
12
30-40 40-50 50-60 60-70 70-80 80-90 90-100
Số ngày đến hạn thanh toán
Số khoản đầu tư ngắn hạn
Bài tập 5
a) Tính tần suất theo công thức: i
i
i
f
df
Đáp án – Nguyên lý thống kê
164 v1.0
Quê quán Số người Tần suất (lần)
Thái Nguyên 2 0,077
Hải Dương 4 0,154
Hà Nội 7
0,269
Lai Châu 1 0,038
Cao Bằng 11
0,423
Nam Định 1
0,038
Tổng 26
1,000
b) Vẽ biểu đồ hình cột (bar chart) cho tần suất.
0.077
0.154
0.269
0.038
0.423
0.038
0
0.2
0.4
0.6
0.8
1
1
Nam Định
Cao Bằng
Lai Châu
Hà Nội
Hải Dương
Thái Nguyên
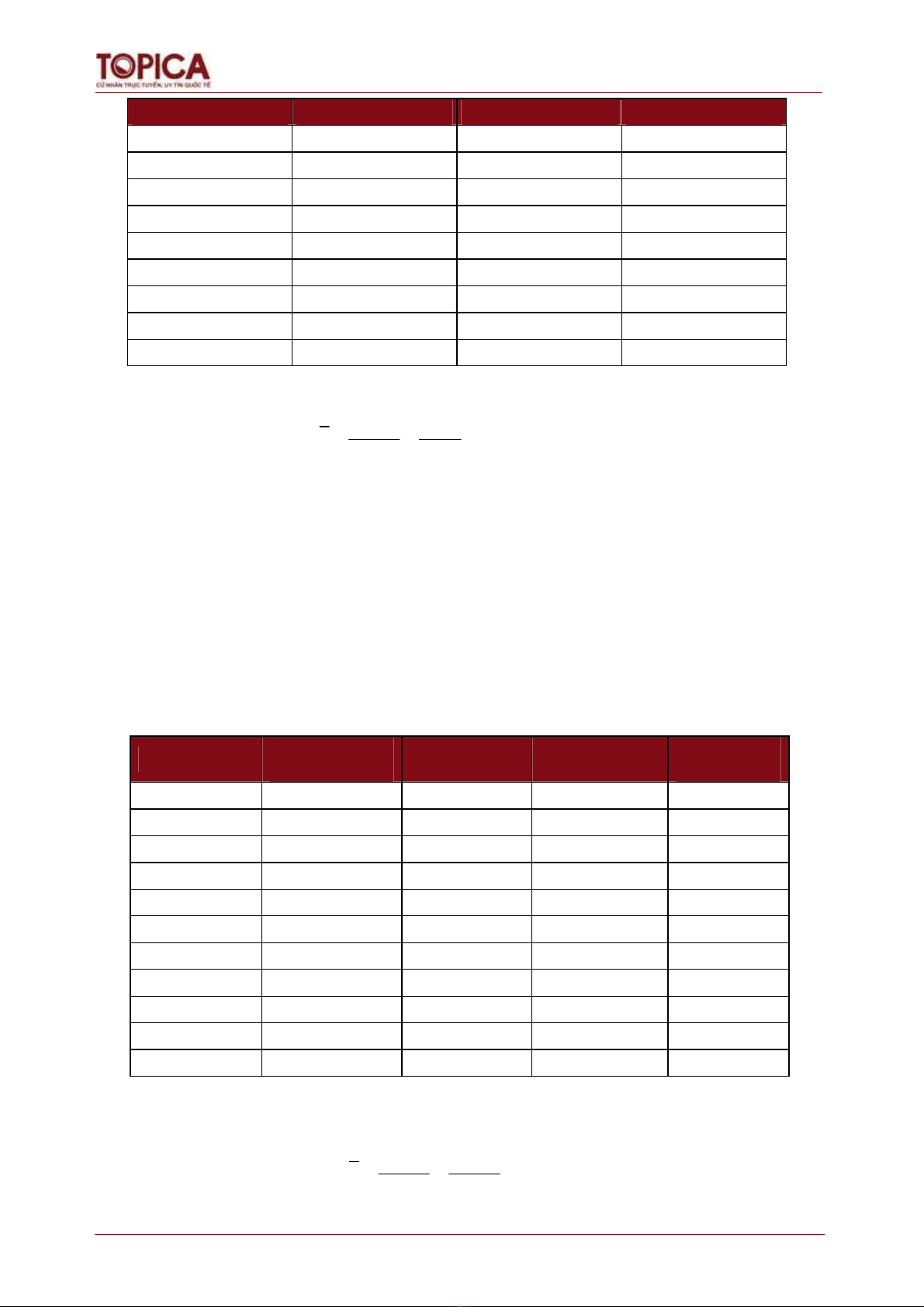
c) Vẽ biểu đồ hình bánh (pie chart) cho tần suất.
Thái Nguyên,
0.077
Hải Dương,
0.154
Hà Nội, 0.269
Lai Châu, 0.038
Cao Bằng, 0.423
Nam Định, 0.038
Thái Nguyên
Hải Dương
Hà Nội
Lai Châu
Cao Bằng
Nam Định
Bài 3
Bài tập 1
a) Bảng tần số phân bố với các tổ không có khoảng cách tổ (chỉ có cột NSLĐ và số công nhân)
Thái Nguyên (0.077)
Hải Dương (0.154)
Nam Định (0.038)
Cao Bằng (0.423)
Lai Châu (0.038) Hà Nội (0.269)
Đáp án – Nguyên lý thống kê
v1.0 165
NSLĐ (sản phẩm) (xi)Số công nhân (fi) xifi Tần số tích luỹ
36 1 36 1
37 3 111 4
38 5 190 9
39 8 312 17
40 5 200 22
41 3 123 25
42 1 42 26
43 4 172 30
Tổng 30 1.186
b) Tính năng suất lao động bình quân của công nhân toàn phân xưởng.
ii
i
xf 1.186
x39,53
f30

(sản phẩm)
c) Tính Mốt về năng suất lao động của công nhân toàn phân xưởng.
Đây là dãy số phân tổ không có khoảng cách tổ, khi đó M0 là lượng biến của tổ có tần số lớn
nhất (fmax = 8), vậy M0 = 39 sản phẩm.
d) Tính trung vị về năng suất lao động của công nhân toàn phân xưởng.
Trung vị là lượng biến của đơn vị đứng ở vị trí chính giữa trong dãy số lượng biến. Có 30
công nhân, vậy vị trí chính giữa là 15 và 16.
Tính tần số tích lũy để xác định vị trí thứ 15 và 16, đó là tổ có lượng biến bằng 39.
Me = (x15 + x16)/2 = (39 + 39)/2 = 39 (sản phẩm)
Bài tập 2
IQ Số trẻ em
(người) (fi) xi xifi Tần số tích luỹ
(di)
60 – 70 1 65 65 1
70 – 80 5 75 375 6
80 – 90 13 85 1.105 19
90 – 100 22 95 2.090 41
100 – 110 28 105 2.940 69
110 – 120 23 115 2.645 92
120 – 130 14 125 1.750 106
130 – 140 3 135 405 109
140 – 150 2 145 290 111
150 – 160 1 155 155 112
112 11.820
a) Đây là dãy số phân tổ có khoảng cách tổ, lượng biến được xác định là trị số giữa của từng tổ (xi).
Khi đó chỉ số IQ bình quân của 112 trẻ em nói trên được tính như sau:
ii
i
xf 1.1820
x 105,54
f 112
