
TR NG THPT HAI BÀ TR NGƯỜ Ư
T Toánổ
H NG D N ÔN T P H C K IƯỚ Ẫ Ậ Ọ Ỳ
MÔN TOÁN L P 12Ớ
Năm h c 2020 - 2021ọ
A- LÝ THUY TẾ
I- Gi i tích:ả
1. S đng bi n ngh ch bi n c a hàm s ự ồ ế ị ế ủ ố 2. C c tr c a hàm sự ị ủ ố
3. Giá tr l n nh t và giá tr nh nh t c a hàm s ị ớ ấ ị ỏ ấ ủ ố 4. Đng ti m c nườ ệ ậ
5. Kh o sát s bi n thiên và v đ th c a hàm s ả ự ế ẽ ồ ị ủ ố 6. Lu th a, hàm s lũy th aỹ ừ ố ừ
7. Lôgarit, hàm s mũ và hàm s lôgaritố ố 8. Ph ng trình, b t ph ng trình mũ và lôgaritươ ấ ươ
II- Hình h c:ọ
1. Khái ni m v kh i đa di n, kh i đa di n l i và kh i đa di n đuệ ề ố ệ ố ệ ồ ố ệ ề
2. Th tích c a các kh i đa di nể ủ ố ệ 3. M t nón, hình nón, kh i nón.ặ ố
4. M t tr , hình tr , kh i tr .ặ ụ ụ ố ụ 5. M t c u, kh i c u.ặ ầ ố ầ
B- BÀI T P:Ậ
1. Các em xem l i các bài t p trong sách giáo khoa và sách bài t p 12.ạ ậ ậ
2. Bài t p tham kh o:ậ ả
CHUYÊN Đ 1: NG D NG ĐO HÀM Đ KH O SÁT VÀ V Đ TH HÀM SỀ Ứ Ụ Ạ Ể Ả Ẽ Ồ Ị Ố
Câu 1. Hàm s ngh ch bi n trên kho ng nào?ố ị ế ả
A. B. C. D.
Câu 2. Hàm s đng bi n trên kho ng nào sau đây ? ố ồ ế ả
A. B. C. D.
Câu 3. Cho hàm s ố
( )
3 2
12 7
3
y x m x mx
= − + + + −
(
m
là tham s ). Xác đnh ố ị
m
đ hàm s ể ố ngh ch bi nị ế trên
t p xác đnh.ậ ị
A. B. C. D.
Câu 4. Cho hàm s , là tham s . Tìm t t c các giá tr c a đ hàm s gi m trên t ng kho ng xác đnh.ố ố ấ ả ị ủ ể ố ả ừ ả ị
A. B. C. D.
Câu 5. Tìm đ hàm s ngh ch bi n trên kho ng . ể ố ị ế ả
A. B. C. D.
Câu 6. Tim m đê ham s nghich biên trên đoan co đô dai băng ố ?
A. . B. C. D.
Câu 7. B ng bi n thiên sau đây là c a hàm s nào?ả ế ủ ố
+ +
.
.
A. .B. .C. .D. .
1
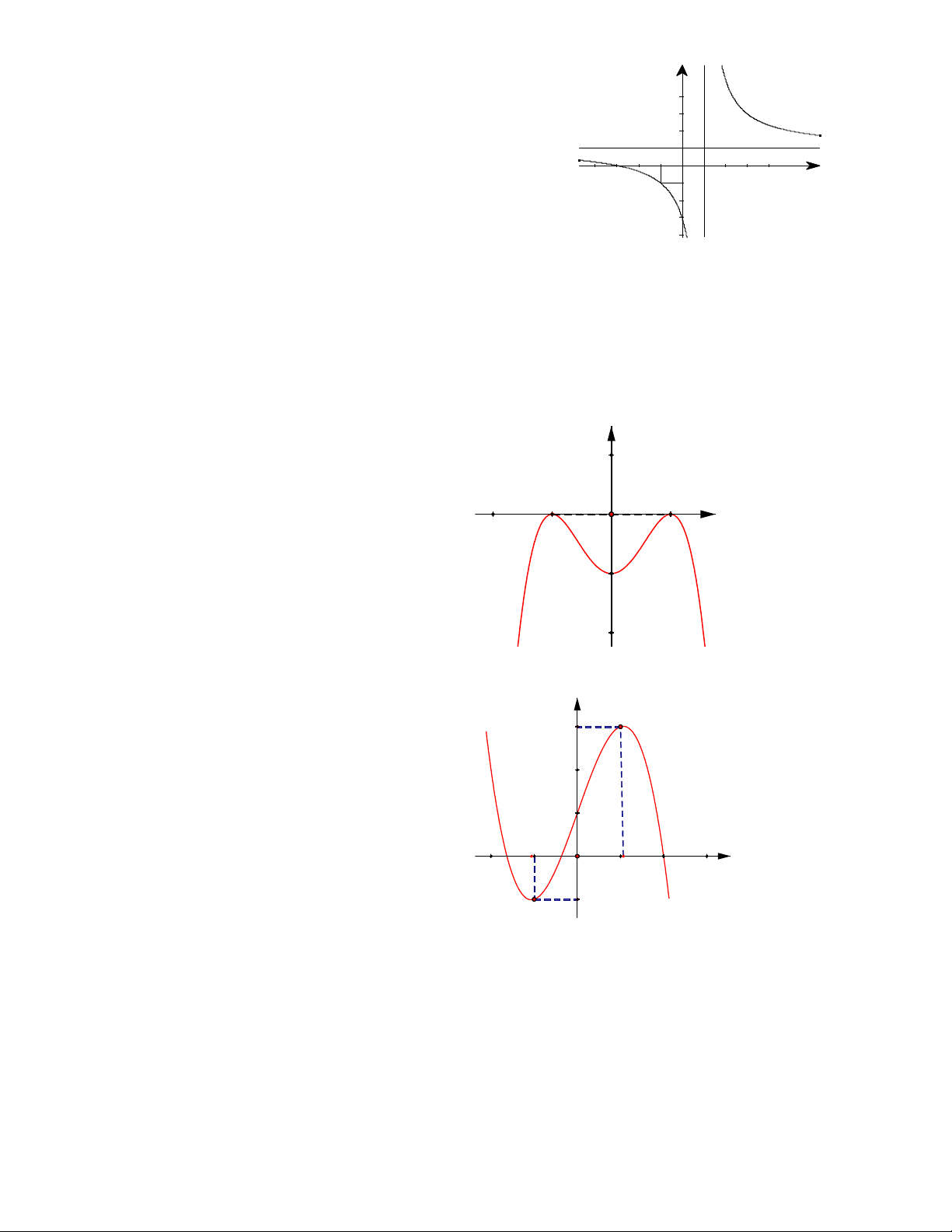
Câu 8. Đng cong hình bên là đ th c a m t hàm s . Hãy ch n kh ng ườ ồ ị ủ ộ ố ọ ẳ
đnh đúng.ị
A. Hàm s đng bi n trên các kho ng và .ố ồ ế ả
B. Hàm s ngh ch bi n trên .ố ị ế
C. Hàm s đng bi n trên .ố ồ ế
D. Hàm s ngh ch bi n trên các kho ng và .ố ị ế ả
x
y
1
1
-1
-1
-3
O
-3
Câu 9. Cho hàm s . Tìm đ hàm s luôn đng bi n trên ố ể ố ồ ế
A. .B. .C. .D. .
Câu 10.Tim tât ca cac gia tri cua m đê ham sô đông biên trên khoang
A. .B. .C. .D. m tuy y.
Câu 11. Cho hàm s V i giá tr nào c a thì hàm s không có c c tr ?ố ớ ị ủ ố ự ị
A. .B. .C. .D. .
Câu 12. Cho hàm s xác đnh,liên t c trên và có đ th nhố ị ụ ồ ị ư
sau. Kh ng đnh nào sau đây là kh ng đnh ẳ ị ẳ ị sai:
A. Hàm s có ba c c tr .ố ự ị
B. Hàm s có giá tr c c ti u b ng .ố ị ự ể ằ
C. Hàm s đt c c đi t i .ố ạ ự ạ ạ
D. Đ th hàm s đi qua đi m .ồ ị ố ể
x
y
1
-2
-1
-2
-1
O
1
Câu 13. Cho hàm s có đ th nh hình v sau, các kh ng đnh sau kh ng đinh nào là đúng?ố ồ ị ư ẽ ẳ ị ẳ
A. Đ th hàm s đt c c đi t i và c c ti u t i .ồ ị ố ạ ự ạ ạ ự ể ạ
B. Hàm s có giá tr c c đi b ng .ố ị ự ạ ằ
C. Hàm s đt giá tr nh nh t b ng và đt giá tr l n nh tố ạ ị ỏ ấ ằ ạ ị ớ ấ
b ng .ằ
D. Đ th hàm s có đi m c c ti uvà đi m c c đi .ồ ị ố ể ự ể ể ự ạ
x
y
1
3
2
-2
-1
-3
-2
-1
3
2
O
1
Câu 14. Cho hàm s . To đ đi m c c đi c a đ th hàm s làố ạ ộ ể ự ạ ủ ồ ị ố
A. B. C. D.
Câu 15. Vi t ph ng trình đng th ng đi qua hai đi m c c tr c a đ th hàm s ế ươ ườ ẳ ể ự ị ủ ồ ị ố
A. B. C. D.
Câu 16. G i là ba ọđi mể c c tr c a đ th hàm s . H i di n tích tam giác là bao nhiêu?ự ị ủ ồ ị ố ỏ ệ
A. . B. . C. . D. .
Câu 17. Tìm t t c các ấ ả giá tr c a tham s đ hàm s có hai c c tr .ị ủ ố ể ố ự ị
2
A. .B. .C. .D. .
Câu 18. Cho hàm số. Tìm t t c các giá tr th c c a đ đ th hàm s có ba đi m c c tr .ấ ả ị ự ủ ể ồ ị ố ể ự ị
A. .B. .C. .D. .
Câu 19. Giá tr đ hàm s : có c c đi, c c ti u làị ể ố ự ạ ự ể
A. . B. . C. . D. .
Câu 20. Tìm t t c các tham s th c đ hàm s có đi m c c tr .ấ ả ố ự ể ố ể ự ị
A. . B. . C. . D. .
Câu 21. Tìm t t c các giá tr th c c a tham s ấ ả ị ự ủ ố
m
đ hàm s không có c c đi.ể ố ự ạ
A. .B. .C. .D. .
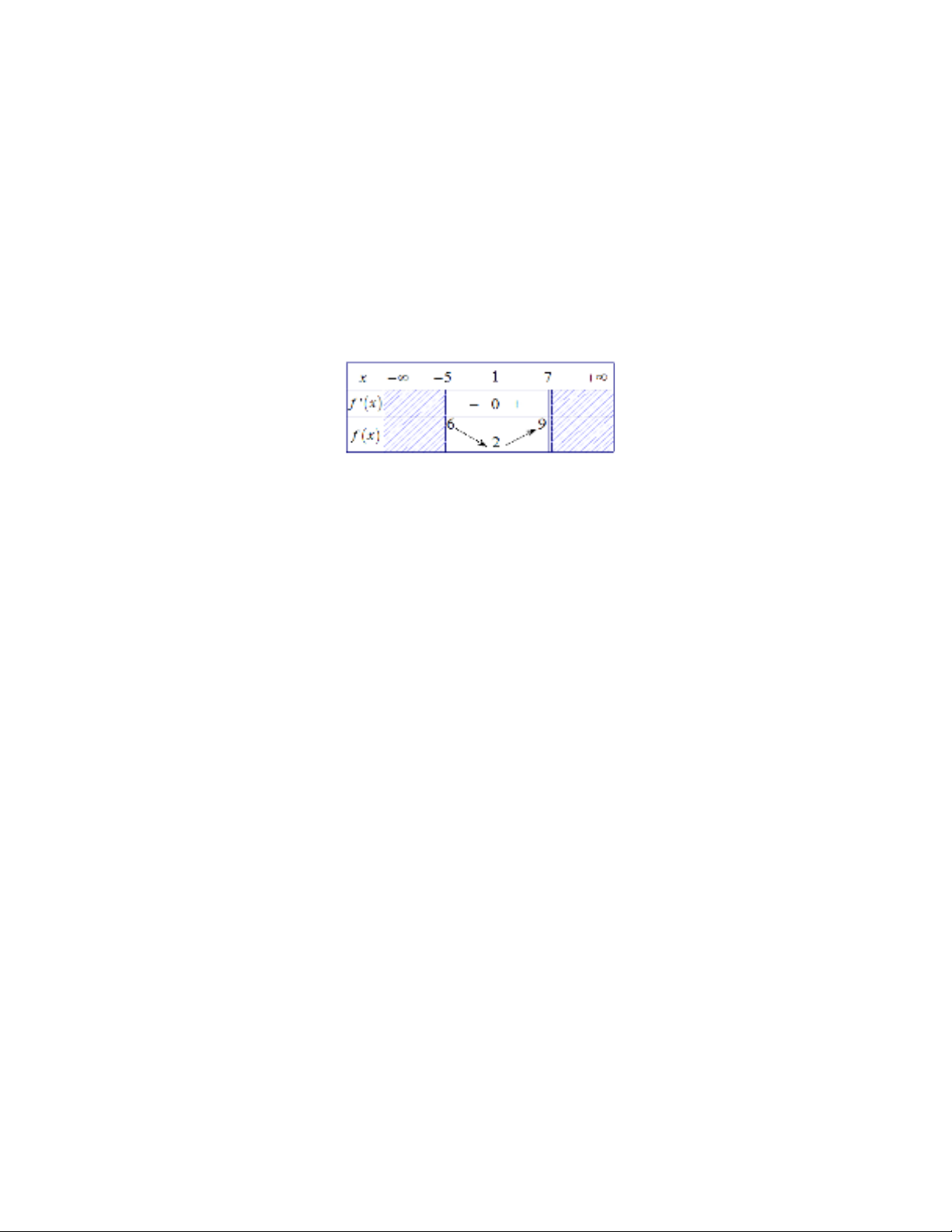
Câu 22.G i và l n l t là giá tr l n nh t và giá tr nh nh t (n u có) c a hàm s trên Bi t hàm s liênọ ầ ượ ị ớ ấ ị ỏ ấ ế ủ ố ế ố
t c và có b ng bi n thiên trên nh hình sau. Hãy ch n m nh đ đúng.ụ ả ế ư ọ ệ ề
A. không t n t i; ồ ạ B.
C. D.
Câu 23. G i là t p giá tr c a hàm s v i . Khi đó ?ọ ậ ị ủ ố ớ
A. . B. . C. . D. .
Câu 24. Bi tế giá tr l n nh t và giá tr nh nh t c a hàm s l n l t là và . K t qu c a làị ớ ấ ị ỏ ấ ủ ố ầ ượ ế ả ủ
A. . B. . C. . D. .
Câu 25. Tìm các giá tr c a đ giá tr c c ti u c a hàm s đt giá tr l n nh t.ị ủ ể ị ự ể ủ ố ạ ị ớ ấ
A. B. C. D.
Câu 26. G i l n l t là giá tr l n nh t và giá tr nh nh t c a hàm s trên đo n .ọ ầ ượ ị ớ ấ ị ỏ ấ ủ ố ạ Giá tr c a làị ủ
A. .B. .C. .D. .
Câu 27. Tìm các giá tr c a đ giá tr c c ti u c a hàm s đt giá tr l n nh t.ị ủ ể ị ự ể ủ ố ạ ị ớ ấ
A. B. C. D.
Câu 28. G i l n l t là giá tr l n nh t và giá tr nh nh t c a hàm s trên đo n . Tính .ọ ầ ượ ị ớ ấ ị ỏ ấ ủ ố ạ
A. . B. . C. . D. .
Câu 29. Tìm đ hàm s đt giá tr nh nh t trên đo n b ng ể ố ạ ị ỏ ấ ạ ằ
A. .B. .C. .D. .
Câu 30. Cho hàm s xác đnh và liên t c trên , có đ thố ị ụ ồ ị
nh hình v bên. Tìm giá tr l n nh t, giá tr nh nh t c aư ẽ ị ớ ấ ị ỏ ấ ủ
hàm s trên đo n .ố ạ
A.
B.
C.
D.
Câu 31: Cho hàm s .S ti m c n c a đ th hàm s b ngố ố ệ ậ ủ ồ ị ố ằ
A.0 B.1 C.2 D.3
Câu 32. Cho hàm s .Kh ng đnh nào sau đây đúng?ố ẳ ị
A.Đ th hàm s có ti m c n ngang là đng th ng. ồ ị ố ệ ậ ườ ẳ B.Đ th hàm s có ti m c n đng là đng th ng .ồ ị ố ệ ậ ứ ườ ẳ
C.Đ th hàm s có ti m c n đng là đng th ng .ồ ị ố ệ ậ ứ ườ ẳ D.Đ th hàm s có ti m c n ngang là đng th ng .ồ ị ố ệ ậ ườ ẳ
3

Câu 33. S đng ti m cân c a đ thi hàm s là:ố ườ ệ ủ ồ ố
A. 1 B. 2 C. 3 D. 4
Câu 34. Đ th hàm s có t t c bao nhiêu đng ti m c n?ồ ị ố ấ ả ườ ệ ậ
A. . B. . C. . D. .
Câu 35. Bi t r ng đ th c a hàm s nh n tr c hoành làm ti m c n ngang và tr c tung làm ti m c n đng. Khi đó giáế ằ ồ ị ủ ố ậ ụ ệ ậ ụ ệ ậ ứ
tr c a là:ị ủ
A. . B. . C. . D. .
Câu 36. Cho hai hàm s và v i . Tìm t t c các giá tr th c d ng c a đ các ti m c n c a hai đ th hàm s t oố ớ ấ ả ị ự ươ ủ ể ệ ậ ủ ồ ị ố ạ
thành m t hình ch nh t có di n tích là .ộ ữ ậ ệ
A. . B. . C. . D. .
Câu 37. S đng ti m c n c a đ th hàm s là ố ườ ệ ậ ủ ồ ị ố
A. . B. . C. . D. .
Câu 38: Cho hàm s . Kh ng đnh nào sau đây đúng v đ th c a hàm s đã cho?ố ẳ ị ề ồ ị ủ ố
A. Có ti m c n ngang là ệ ậ B. Có ti m c n ngang là ệ ậ
C. Không có ti m c n đng.ệ ậ ứ D. Có hai ti m c n đng là ệ ậ ứ
Câu 39: Cho hàm s ố. V i giá tr nào c a m ớ ị ủ thì đng ườ ti m c n đng ệ ậ ứ , ti m c n ngang c a đ th hàm s cùng haiệ ậ ủ ồ ị ố
tr c t a đ t o thành m t hình ch nh t có di n tích b ng 8.ụ ọ ộ ạ ộ ữ ậ ệ ằ
A. B. C. D.
Câu 40: Cho hàm s . Tìm t t c các giá tr th c c a tham s đ đ th hàm s có 4 đng ti m c n.ố ấ ả ị ự ủ ố ể ồ ị ố ườ ệ ậ
A. B. C. D.
KH O SÁT S BI N THIÊN VÀ V Đ TH HÀM SẢ Ự Ế Ẽ Ồ Ị Ố
Câu 41: Đ th hàm s có d ng:ồ ị ố ạ
A B C D
Câu 42: Đ th hàm s có d ng:ồ ị ố ạ
A B C D
4

Câu 43: Đ th hàm s có d ng:ồ ị ố ạ
A B C D
Câu 44: Đ th hình bên là c a hàm s :ồ ị ủ ố
A.
B.
C.
D.
Câu 45: Đ th hình bên là c a hàm s :ồ ị ủ ố
A. B.
C. D.
Câu 46: Đ th hình bên là c a hàm s :ồ ị ủ ố
A. B.
C. D.
Câu 47: Cho hàm s có đ th nh hình v :ố ồ ị ư ẽ
5





![Bài tập so sánh hơn và so sánh nhất của tính từ [kèm đáp án/mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250808/nhatlinhluong27@gmail.com/135x160/77671754900604.jpg)
![Tài liệu tham khảo Tiếng Anh lớp 8 [mới nhất/hay nhất/chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250806/anhvan.knndl.htc@gmail.com/135x160/54311754535084.jpg)




![Tài liệu Lý thuyết và Bài tập Tiếng Anh lớp 6 [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250802/hoihoangdang@gmail.com/135x160/18041754292798.jpg)




