Mã đề 161 Trang 1/4
SỞ GD & ĐT QUẢNG TRỊ
TRƯỜNG PHỔ THÔNG DTNT TỈNH
ĐỀ KIỂM TRA GIỮA KỲ II – NĂM HỌC 2024-2025
MÔN TOÁN LỚP 12
Thời gian làm bài: 90 Phút; (Không kể thời gian giao đề)
Đ
Ề CHÍNH THỨC
(Đ
ề có
04
trang
)
H
ọ t
ên :
............................................................... L
ớp : .............
......
Mã đề thi: 161
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 16. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1. Tính
2
0
2 d
x
x
.
A.
3
ln2
. B.
2
ln 2
. C.
4
ln 2
. D.
1
ln 2
.
Câu 2. Cho hàm số
( )
F x
là một nguyên hàm của hàm số
( )
f x
trên
K
. Các mệnh đề sau, mệnh đề nào
sai.
A. ( ) ( )
f x dx F x C
. B.
( ) ( )
f x dx F x
.
C.
( ) ( )
f x dx f x
. D.
( ) ( )
f x dx F x C
.
Câu 3. Cho hàm số
, ,
y f x y g x
liên tục trên khoảng
K
và
, , ; ;
a b c K b a c
. Mệnh đề nào sau
đây sai?
A.
. d d
b b
a a
k f x x k f x x
. B.
d d d
b b b
a a a
f x g x x f x x g x x
.
C.
d d d
b b c
a c a
f x x f x x f x x
. D.
d d d
b b a
a a b
f x g x x f x x g x x
.
Câu 4. Cho hai hàm số
( )
f x
và
( )
g x
liên tục trên
;
a b
. Diện tích hình phẳng giới hạn bởi đồ thị của các
hàm số
( )
y f x
,
( )
y g x
và các đường thẳng
x a
,
x b
bằng
A.
( ) ( ) d
b
a
f x g x x
. B.
( ) ( ) d
b
a
f x g x x
.
C.
( ) ( ) d
b
a
f x g x x
. D.
( ) ( ) d
b
a
f x g x x
.
Câu 5. Cho hàm số
f x
thỏa mãn
4 3cos
f x x
và
2
2
f
. Mệnh đề nào dưới đây đúng?
A.
4 3sin 3
f x x x
. B.
4 3sin 3
f x x
.
C.
4 3sin 3
f x x x
. D.
4 3sin 3
f x x x
.
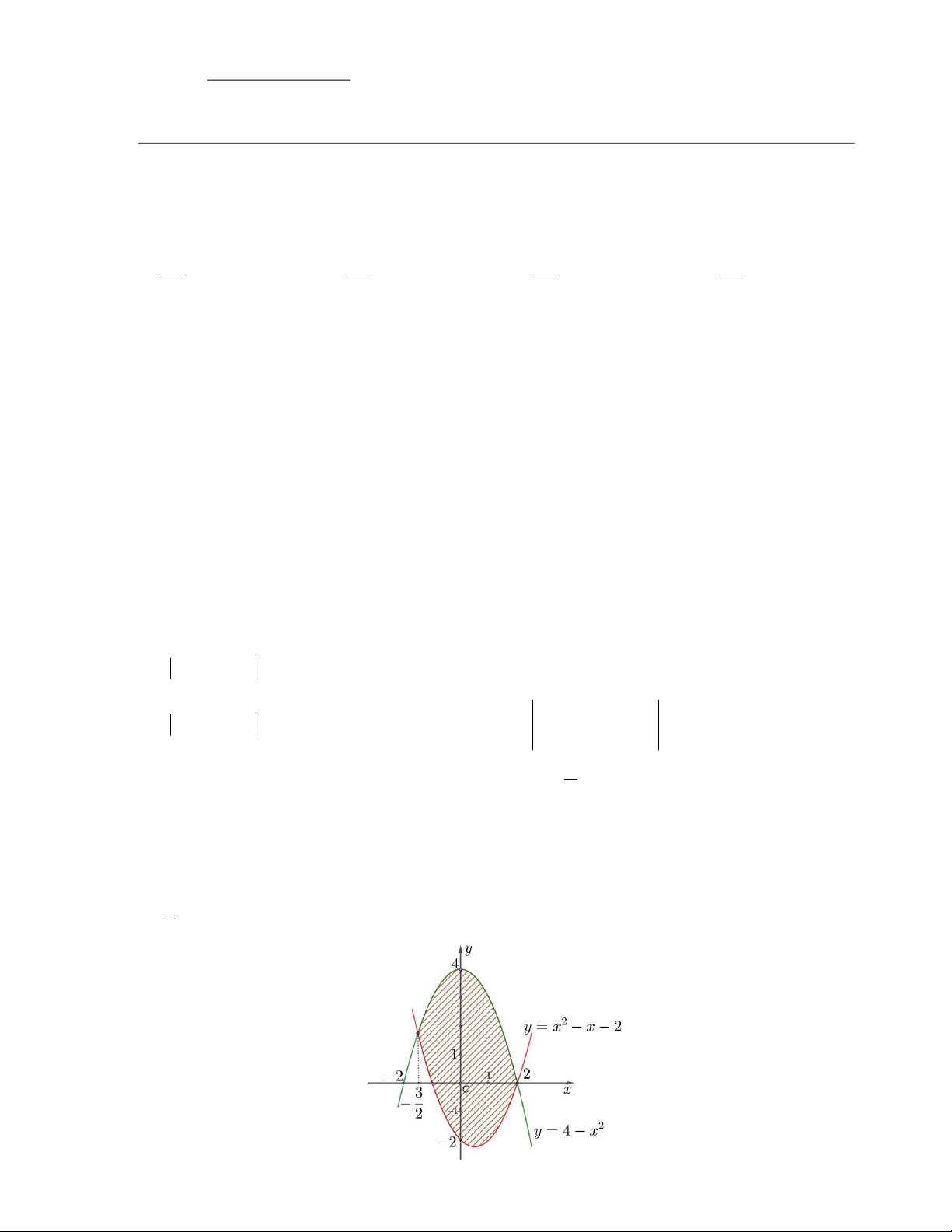
Câu 6. Tính diện tích hình phẳng giới hạn bởi hai parabol 2
2
y x x
,
2
4
y x
và hai đường thẳng
3
,
2
x
2
x
(hình vẽ).