PHÒNG GIÁO DỤC VÀ ĐÀO TẠO MA TRÂN ĐỀ KIỂM TRA GIỮA HKII NĂM HỌC 2022-2023
TRƯỜNGTHCS NGUYỄN CÔNG TRỨ MÔN : TOÁN – LỚP 9
Thời gian làm bài: 90 phút
Cấp độ
Chủ đề Nhận biết Thông
hiểu
Vận dụng Cộng
Cấp độ thấp Cấp độ cao
1. ĐS –
Phương trình
bậc hai,HPT
- Giải phương trình
bậc hai một ẩn (dạng
đơn giản) bằng cách
tính nhẩm nghiệm
hoặc dùng công thức
nghiệm.
Các bài toán
liên quan
đến phương
trình
Số câu – Số
điểm
1câu 1đ 2câu đ 3câu 3đ
2.ĐS – Hàm số
y = ax2 (a≠0)
Phương trình
bậc hai một ẩn
- Vẽ đồ thị hàm số y = ax2 (cho a ∈ Z hoặc a∈ Q, a ≠ 0)
- Bài toán liên quan đến giao điểm của parabol và đường
thẳng.
- Giải bài toán bằng cách lập hệ phương trình
Số câu – Số
điểm
2câu 2đ 1câu 1.5đ 3 câu 3đ
Bất đảng thức
HPT nâng cao
Sử dụng BĐT để
tìm GTNN,GTLL
Số câu – Số
điểm
1 câu 0.5đ 1 câu 0.5đ
3.Hình –
Chương III:
Góc và đường
tròn
-Vẽ hình đúng theo giả thiết bài toán.
- Vận dụng tính chất các loại góc có liên quan đến đường
tròn, các kiến thức về tứ giác nội tiếp để chứng minh các
đặc tính hình học.
- Vận dụng linh hoạt các tính chất về góc và đường tròn, tứ
giác nội tiếp,… để làm bài tập nâng cao
Số câu – Số
điểm
1câu 0,5đ 2 câu 1.75đ 1câu 0,75đ 4 câu 3,5đ
Tổng
Tỉ lệ %
4 câu 3,5đ
35%
5 câu 5,25đ
52,5%
2câu 1.25đ
12.5%
11câu 10đ
100%
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HUYỆN LONG ĐIỀN
ĐỀ KIỂM TRA GIỮA HỌC KỲ II.NĂM HỌC 2022-2023
MÔN : TOÁN – LỚP 9
TRƯỜNGTHCS NGUYỄN CÔNG TRỨ Thời gian 90 phút (không kể thời gian phát đề)
Câu 1 : (3,0điêLm) Giải các phương trình và hệ phương trình sau:
1 ) x2 – 7x +12 = 0. 2) x2 – 8x + 16 = 0 3)
3 4
2 6
x y
x y
+ =
− =
Câu 2 : (1,5 điêLm) Cho parabol (P): y =
2
2
x
và đường thẳng
( )
d : y x 2m= +
(m là tham số)
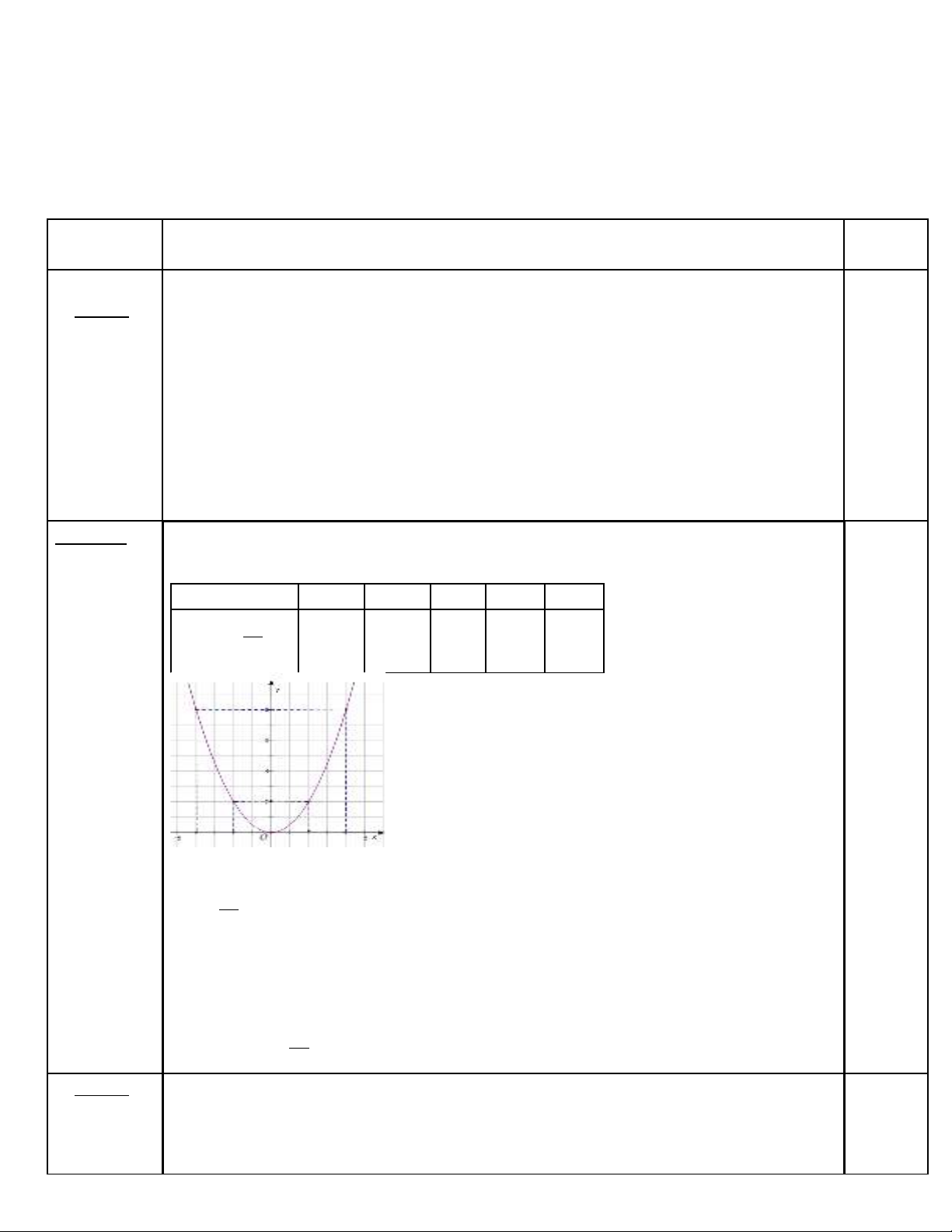
1/ Vẽ đồ thị của (P).
2/ Tìm giá trị m để (P) và (d) cắt nhau tại hai điểm phân biệt.
Câu 3 : (1,5 điêLm) Giải bài toán sau :
Một khu vườn hình chữ nhật có chiều dài gấp ba lần chiều rộng và chu vi của khu vườn
bằng 120m. Tính diên tích khu vườn.
Câu 4 :(3,5 điêLm) Cho đường tròn (O) đường kính BC, A là một điểm thuộc (O) sao cho AB
< AC, D là điểm giữa O và C. Đường thẳng vuông góc với BC tại D cắt AC tại E và cắt
đường thẳng AB tại F.
1) Chứng minh các tứ giác ABDE nội tiếp.
2) Tiếp tuyến tại A của (O) cắt DE tại M. Chứng minh:
ˆ ˆ
AEF ABC
=
.
3) Chứng minh AME cân tại M.
4) Gọi I là tâm đường tròn ngoại tiếp tứ giác ADCF. Chứng minh OI vuông góc với AC.
Câu 5 :(0.5 điêLm) Giải hệ phương trình:
2
1 1 1 2
x y z
2 1 4
xy z
+ + =
− =
Hết
(Giám thị không giải thích gì thêm)
ĐỀ CHÍNH THỨC
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO ĐÁPÁN ĐỀ KIỂM TRA HKII NĂM HỌC 2022-2023
TRƯỜNGTHCS NGUYỄN CÔNG TRỨ MÔN : TOÁN – LỚP 9
Thời gian 90 phút (không kể phát đề)
Câu Nội Dung Thang
Điểm
Câu 1:
(3 điêLm)
1) Giải phương trình :
x2 – 7x +12 = 0
=b2- 4ac= 1 PT có 2 nghiệm P/B
x = 4 ; x = 3
2) Giải phương trình :
x2 – 8x + 16 = 0.
= 0 PT có nghiệm kép x =4
3)
3 4
2 6
x y
x y
+ =
− =
5 10
3 4
x
x y
=
+ =
0.5
0.5
0,5x2
0.5
0.5
Câu 1,5:
(1.5 điêLm)
a/ Vẽ đồ thị của (P) hệ trục tọa độ Oxy
Bảng giá trị
x -4 -2 0 2 4
y =
2
2
x
8 2 0 2 8
b) Tọa độ giao điểm (P) và (d) là nghiệm của PT
22
'
2 2 4 0
2
1 4
xx m x x m
m
= + − − =
∆ = +
Để (P) và (d) cắt nhau tại hai điểm phân biệt.
'1
04
m−
∆ > >
0,25
0,75
0,25
0,25
Câu 3:
(1,5 điêLm)
Gäi chiÒu dµi cña khu vườn lµ x(m)
ChiÒu réng cña khu vườn lµ y(m) ( x>0, x>y)
0,25
0,25
0,5
=>
3
2( ) 120
x y
x y
=
+ =
Gi¶i hÖ ta ®îc x = 45, y = 15 (tho¶ m·n)
VËy diÖn tÝch cña khu vườn lµ: 45.15 = 675(m2).
0.25
0.25
Câu 4:
(3,5 điêLm)
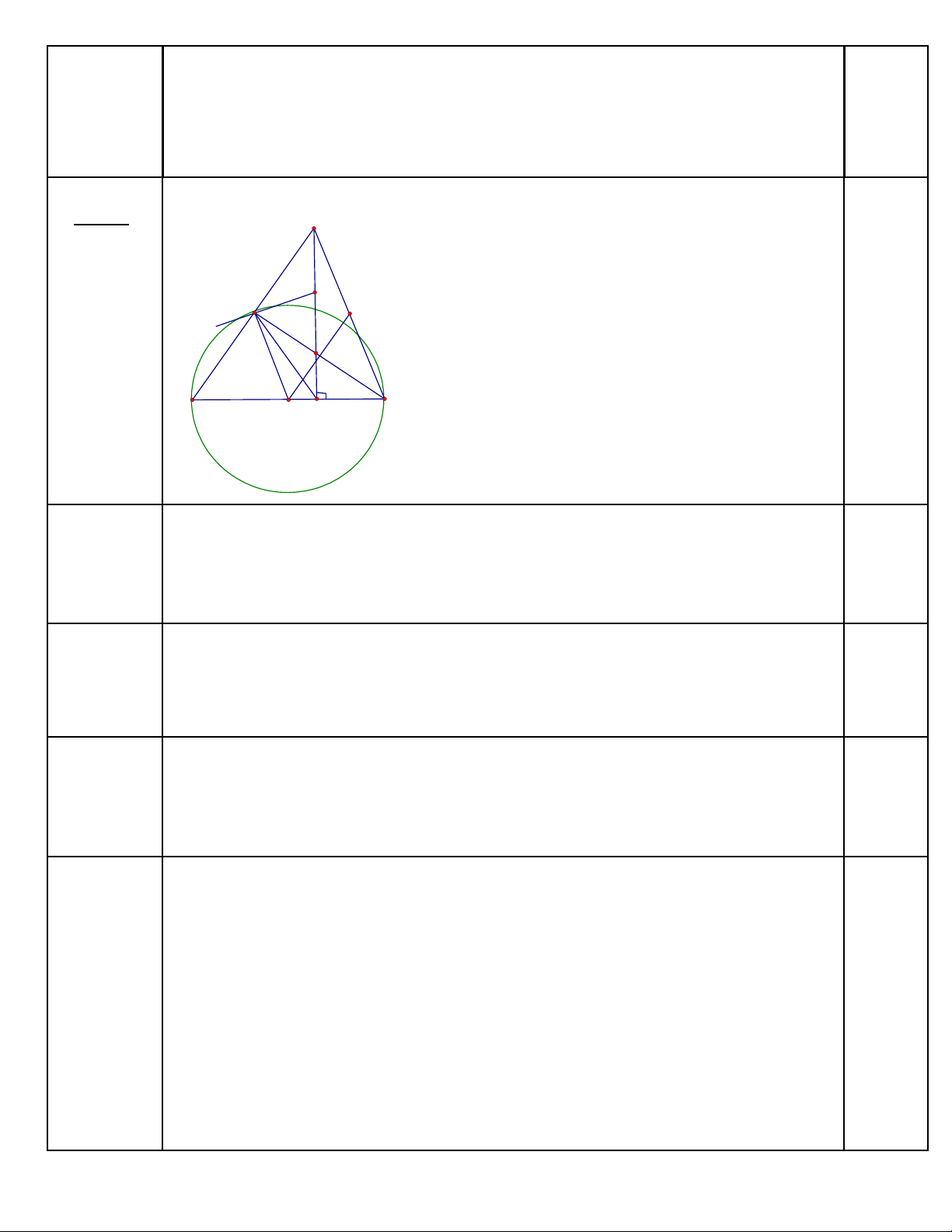
Vẽ hình đúng
E
I
A
O
C
F
B
D
M
0, 5
1)
Chứng minh tứ giác ABDE nội tiếp đường tròn
0
ˆ90BAE =
( góc nội tiếp chắn nửa đường tròn (O))
0
ˆ90BDE =
(gt)
Tứ giác ABDE có
0
ˆˆ180BAE BDE+ =
nên nội tiếp đường tròn
0, 5
0, 5
2)
Chứng minh:
ˆ ˆ
AEF ABC=
0
ˆ ˆ 180AEF AED+ =
( 2 góc kề bù)
0
ˆ ˆ 180ABC AED+ =
(ABDE là tứ giác nội tiếp)
Suy ra
ˆ ˆ
AEF ABC=
0, 25
0,25
0,25
3)
Chứng minh tam giác AME cân tại M.
ˆˆ
MAE ABC=
(cùng chắn cung AC của đường tròn O)
ˆ ˆ
AEF ABC=
(cmt)
Suy ra
ˆˆ
MAE AEF=
hay AME cân tại M.
0, 25
0,25
0,25
4)
Xét tứ giác ADCF nội tiếp đường tròn
0
ˆ90FAC =
(Kề bù với
0
ˆ90BAE =
)
0
ˆ90FDC =
(gt)
Tứ giác ADCF có 2 đỉnh A và D kề nhau cùng nhìn cạnh CF dưới một góc
bằng nhau nên là tứ giác nội tiếp.
Tứ giác ADCF nội tiếp (cmt) mà
ˆ
CDF
=900 (gt)
CF là đường kính của đường tròn ngoại tiếp tứ giác ADCF.
Vậy tâm I của đường tròn ngoại tiếp tứ giác ADCF là trung điểm của CF
Tam giác BCF có : OI là đường trung bình nên OI//AB
Mà AB AC tại A
OI AC
0.25
0.25
Câu 5:
2
1 1 1 2 (1)
( ) 2 1 4 (2)
x y z
I
xy z
+ + =
− =
Từ (1)
2 2 2
1 1 1 2 2 2 4
x y z xy xz yz
+ + + + + =
Thế vào (2) ta được:
2 2 2 2
2 1 1 1 1 2 2 2
xy z x y z xy xz yz
− = + + + + +
2 2 2
1 1 2 2 2 0
x y z xz yz
+ + + + =
2 2 2 2
1 2 1 1 2 1
( ) ( ) 0
x xz z y yz z
+ + + + + =
2
2
1 1 1 1 0
x z y z
+ + + =
1 1 0
1 1 0
x z x y z
y z
+ =
= = −
+ =
Thay vào hệ (I) ta được:
1 1 1
( ; ; ) ( ; ; ) ( )
2 2 2
x y z TM= −
0,25
0,25
* Lưu ý: Học sinh giải cách khác đúng vẫn cho tròn điểm