UBND HUYỆN CỦ CHI
TRƯỜNG THCS PHÚ HÒA ĐÔNG
ĐỀ KIỂM TRA CUỐI KỲ I
NĂM HỌC 2023-2024
MÔN: TOÁN HỌC – KHỐI LỚP 8
Thời gian làm bài: 90 phút (không tính thời gian giao đề)
Bài 1 (3 điểm). Thực hiện phép tính
( )( )
a) 4 5 3 7xyx y−+
53 4 3 3
b) (12 18 6 ) : 6xy xy xy xy−+
5 37 3
c) 44
xx−+
+
2
46 1
d) 33
9
xx
xx
x
−
−+
+−
−
Bài 2 (1,5 điểm). Phân tích các đa thức sau thành nhân tử
2
a) 2 14xx−
2
b) 25 10 1yy−+
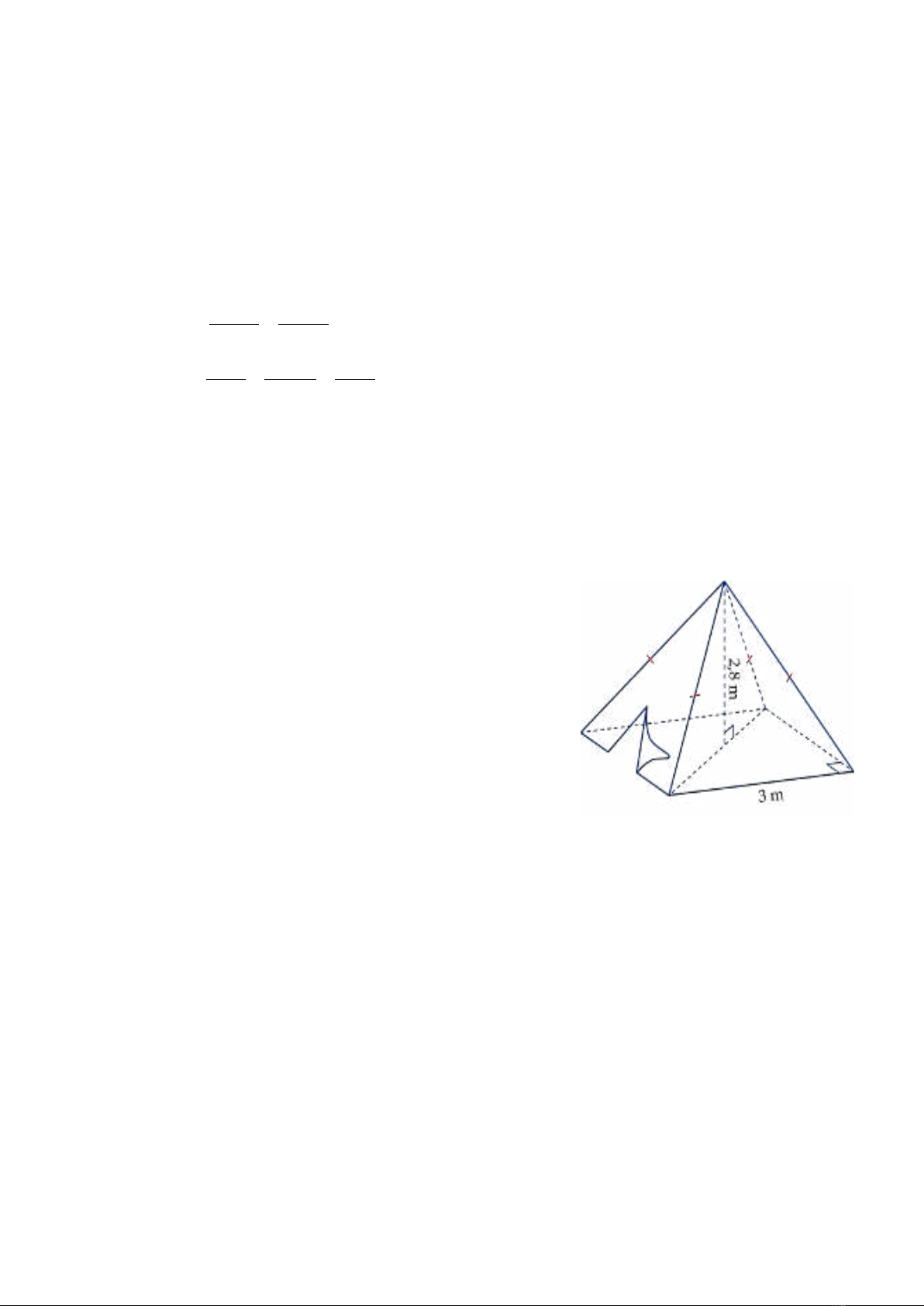
Bài 3 (1,0 điểm). Một chiếc lều có dạng hình chóp tứ
giác đều, biết độ dài cạnh đáy là 3m, chiều cao của
hình chóp là 2,8 m .
a) Tính thể tích không khí trong chiếc lều .
b) Biết độ dài chiều cao của mặt bên hình chóp là
2,5m. Hỏi phải trả ít nhất bao nhiêu tiền để mua tấm
bạt phủ kín chiếc lều ( không tính mặt tiếp giáp với đất
và các mép nối không đáng kể) biết giá bạt
2
1 42000m
đồng.
Bài 4 (1,0 điểm). Một cửa hàng văn phòng phẩm nhập 3 cái máy tính CASIO FX-
880BTG với giá vốn là 750 000 đồng /chiếc. Sau đó cửa hàng bán ra với giá lời 15% so
với giá vốn. Hỏi sau khi bán hết 3 cái máy, cửa hàng lãi được bao nhiêu tiền ?
Bài 5 (1,0 điểm). Nhân dịp Tết Âm lịch 2022, siêu thị Điện máy xanh bán hàng khuyến
mãi giảm giá 15% cho một cái tủ lạnh hiệu TOSHIBA. Mẹ Hồng là khách hàng thân
thiết nên được giảm thêm 8% trên giá đã giảm. Hỏi sau 2 lần giảm giá thì Mẹ Hồng phải
trả bao nhiêu tiền cho một cái tủ lạnh, biết rằng giá ban đầu là 15 000 000 đồng ?
Bài 6. (2,5 điểm). Cho
∆
ABC vuông tại A (AB < AC) có AH là đường cao của
∆
ABC.
Gọi E, F, M lần lượt là trung điểm của AB, AC và BC.
a) Trên tia đối của tia FH lấy điểm N sao cho F là trung điểm của HN. Chứng minh:
Tứ giác AHCN hình chữ nhật.
b) Trên tia đối của tia EM lấy điểm D sao cho ME = DE. Chứng minh: Tứ giác ADBM
hình thoi.
c) Chứng minh:
HE HF⊥
.
_________Hết________
ỦY BAN NHÂN DÂN HUYỆN CỦ CHI
TRƯỜNG THCS PHÚ HÒA ĐÔNG
ĐÁP ÁN – THANG ĐIỂM
Môn thi: TOÁN 8
(Đáp án – Thang điểm có 02 trang)
Bài
Đáp án
Điểm
1
( )( )
2 22 2
a) 4 5 3 7 12 28 15 35 12 7 35x y x y x xy xy y x xy y− += + − − = +−
53 4 3 3 22
b) (12 18 6 ) : 6 2 3 1xy xy xy xy xy x− + = −+
5373537312
c) 3
44 4 4
x x xx x
x
− + −+ +
+= ==
2
46 1
d) 33
9
xx
xx
x
−
−+
+−
−
( 3) 4 6 3
( 2)( 2)
xx x x
xx
− − +++
=−+
2
69
( 3)( 3)
xx
xx
−+
=+−
3
3
x
x
−
=+
0,25x3
0,25x3
0,25x3
0,25x3
2
( )
2
a) 2 14 2 7x x xx−= −
( )
2
2
b) 25 10 1 5 1yy y− += −
( )
( ) ( )
( )( )
22
22 2 2
c) 9 4 4 9 4 4 3 2
3232
yx x y x x y x
yx yx
− + −= − − + = − −
= +− −+
0,5
0,5
0,25
0,25
3
a) Thể tích không khí trong chiếc lều là
( )
23
13 .2,8 8, 4
3cm⋅=
b) Diện tích xung quanh của chiếc liều là
( )
2
1
4 3.2,5 15
2cm⋅⋅ =
Số tiền để mua tấm bạt phủ kín chiếc lều là
15.42000 = 630000 (đồng)
Vậy phải trả ít nhất 630000 đồng để mua tấm bạt phủ kín chiếc lều (
không tính mặt tiếp giáp với đất và các mép nối không đáng kể).
0,5
0,25
0,25
4
Sau khi bán hết 3 cái máy, cửa hàng lãi được:
3.750000.15% = 337 500 (đồng)
1,0
5
Sau 2 lần giảm giá thì Mẹ Hồng phải trả bao nhiêu tiền cho một cái tủ
lạnh là
15000000.75%.92% = 11 730 000 (đồng)
1,0
6
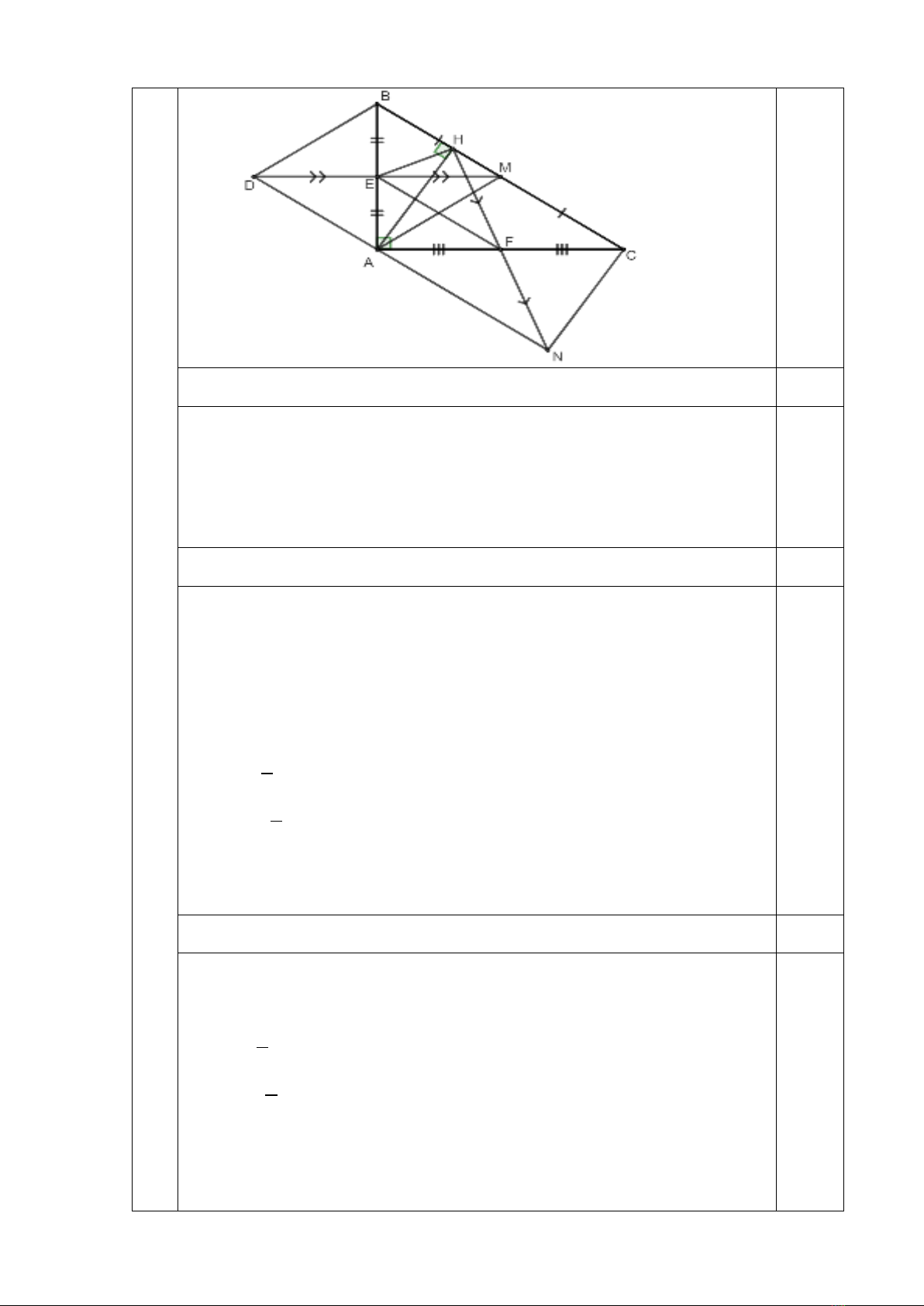
a) Chứng minh: Tứ giác AHCN hình chữ nhật.
Xét tứ giác AHCN ta có:
F là trung điểm của AC (gt)
F là trung điểm của HN (gt)
Vậy tứ giác AHCN hình bình hành.
Mà 𝐴𝐴𝐴𝐴𝐴𝐴
�= 900 (gt)
Nên tứ giác AHCN hình chữ nhật
0,5
0,25
0,25
b) Chứng minh: Tứ giác ADBM hình thoi.
Xét tứ giác ADBM ta có:
E là trung điểm của AB (gt)
E là trung điểm của MD (ME = DE)
Vậy tứ giác ADBM hình bình hành. (1)
Xét
ABC∆
vuông tại A ta có:
AM là đường trung tuyến ứng với cạnh huyền BC ( M là trung điểm
của BC)
1
2
AM BC⇒=
Mà
1
2
BM BC=
(M là trung điểm của BC)
AM BM⇒=
(2)
Từ (1) và (2)
⇒
Tứ giác ADBM hình thoi
0,25
0,25
0,25
0,25
c) Chứng minh:
HE HF⊥
.
Xét
ABH∆
vuông tại H ta có:
HE là đường trung tuyến ứng với cạnh huyền AB ( E là trung điểm của
AB)
1
2
HE AB⇒=
Mà
1
2
AE AB=
(E là trung điểm của AB)
HE AE⇒=
Chứng minh tương tự:
HF AF=
Xét
EAF∆
và
EHF∆
ta có:
AE = HE (cmt)
0,25
EF là cạnh chung
AF = HF (cmt)
Vậy
EAF∆
=
EHF∆
(c.c.c)
⇒
𝐸𝐸𝐴𝐴𝐸𝐸
�=𝐸𝐸𝐴𝐴𝐸𝐸
�
Mà 𝐸𝐸𝐴𝐴𝐸𝐸
�=900 (gt)
Nên 𝐸𝐸𝐴𝐴𝐸𝐸
�=900
Vậy
HE HF⊥
0,25
Chú ý: Học sinh làm sử dụng kiến thức khác đã được học trong chương trình làm đúng vẫn
cho điểm tối đa.