SỞ GD & ĐT ĐỒNG THÁP
TRƯỜNG THPT LẤP VÒ 1
ĐỀ THI HỌC KÌ 2 – Năm học 2012 – 2013
Môn TOÁN Lớp 11
Thời gian làm bài 90 phút
I. Phần chung: (8,0 điểm)
Câu 1: (2,0 điểm) Tìm các giới hạn sau:
a)

nn
nn
3
32
2 3 1
lim 21
b)
x
x
x
0
11
lim

Câu 2: (1,0 điểm) Tìm a để hàm số sau liên tục tại điểm x = 0:
x a khi x
fx x x khi x
220
() 10

Câu 3: (2,0 điểm) Tính đạo hàm của các hàm số sau:
a)
y x x
2.cos
b)
y x x2
( 2) 1
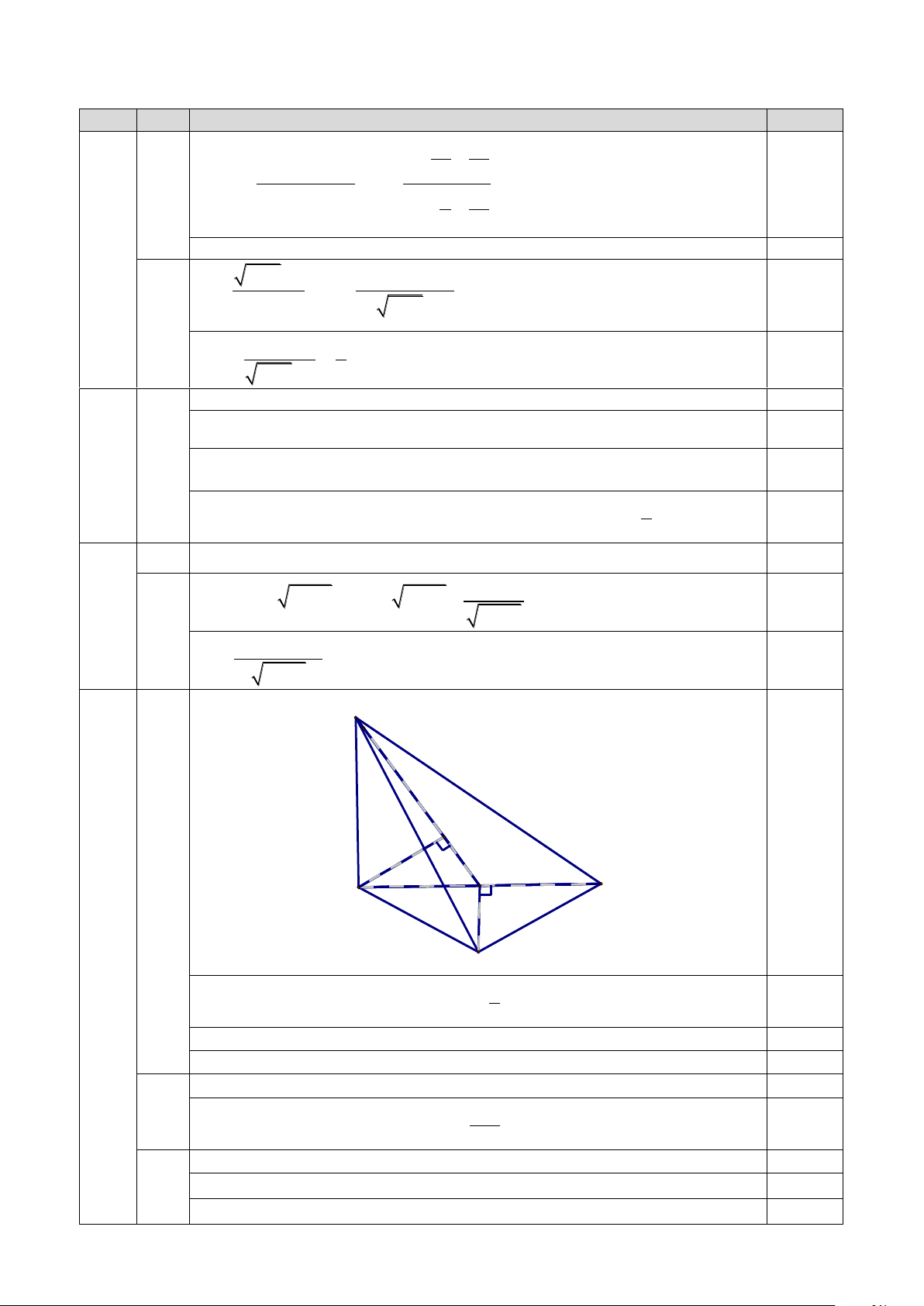
Câu 4: (3,0 điểm) Cho tam giác đều ABC cạnh bằng a. Trên đường thẳng vuông góc với
mặt phẳng (ABC) tại B, ta lấy một điểm M sao cho MB = 2a. Gọi I là trung điểm của
BC.
a) (1,0 điểm) Chứng minh rằng AI (MBC).
b) (1,0 điểm) Tính góc hợp bởi đường thẳng IM với mặt phẳng (ABC).
c) (1,0 điểm) Tính khoảng cách từ điểm B đến mặt phẳng (MAI).
II. Phần riêng: (2,0 điểm) học sinh chỉ được chọn một trong hai phần sau
1. Theo chương trình Chuẩn
Câu 5a: (1,0 điểm) Chứng minh rằng phương trình sau luôn có nghiệm với mọi m:
m x x x
3
( 1) ( 2) 2 3 0
Câu 6a: (1,0 điểm) Cho hàm số
y f x x x x
32
( ) 3 9 5
.Viết phương trình tiếp tuyến với
đồ thị hàm số tại điểm có hoành độ bằng 1.
2. Theo chương trình Nâng cao
Câu 5b: (1,0 điểm) Chứng minh rằng phương trình sau luôn có nghiệm với mọi m:
m m x x
24
( 1) 2 2 0
Câu 6b: (1,0 điểm) Cho hàm số
.Viết phương trình tiếp tuyến với
đồ thị hàm số, biết tiếp tuyến có hệ số góc bằng 6.
––––––––––––––––––––Hết–––––––––––––––––––
ĐÁP ÁN ĐỀ KIỂM TRA HỌC KÌ II – NĂM HỌC 2012 – 2013
MÔN TOÁN LỚP 11
CÂU
Ý
NỘI DUNG
ĐIỂM
1
a)



nn nn
Inn
nn
323
32
3
31
2
2 3 1
lim lim 21
21 1
0,50
I = -2
0,50
b)
00
11
lim lim 11
xx
xx
xxx


0,50
0
11
lim 2
11
xx


0,50
2
f(0) = 1
0,25
0
lim ( ) 1
x
fx
0,25
xx
f x x a a
00
lim ( ) lim( 2 ) 2


0,25
f(x) liên tục tại x = 0


00
1
lim ( ) lim ( ) (0) 2
xx
f x f x f a
0,25
3
a)
22
cos ' 2 cos sinxy x x y x x x
1,00
b)
xx
y x x y x
x
22
2
( 2)
( 2) 1 ' 1 1
0,50
2
2
2 2 1
'1
xx
y
x

0,50
4
a)
I
B
C
A
M
H
0,25
Tam giác ABC đều cạnh a , IB = IC =
a
2
AI BC (1)
0,25
BM (ABC) BM AI (2)
0,25
Từ (1) và (2) ta có AI (MBC)
0,25
b)
BM (ABC) BI là hình chiếu của MI trên (ABC)
0,50
MB
MI ABC MIB MIB IB
,( ) , tan 4
0,50
c)
AI (MBC) (cmt) nên (MAI) (MBC)
0,25
MI MAI MBC BH MI BH MAI( ) ( ) ( )
0,25
d B MAI BH( ,( ))
0,25
2 2 2 2 2 2
1 1 1 1 4 17 2 17
17
44
a
BH
BH MB BI a a a
0,25
5a
Gọi
f x m x x x
3
( ) ( 1) ( 2) 2 3
fx()
liên tục trên R
0,25
f(1) = 5, f(–2) = –1 f(–2).f(1) < 0
0,50
PT
fx( ) 0
có ít nhất một nghiệm
c m R( 2;1),
0,25
6a
00
16xy
0,25
' 1 12kf
0,50
Phương trình tiếp tuyến cần tìm là: y = –12x + 6
0,25
5b
Gọi
f x m m x x
24
( ) ( 1) 2 2
fx()
liên tục trên R
0,25
f(0) = –2, f(1) =
2
213
10
24
m m m



f(0).f(1) < 0
0,5
Kết luận phương trình
fx( ) 0
đã cho có ít nhất một nghiệm
cm(0;1),
0,25
6b
Gọi
xy
00
( ; )
là toạ độ của tiếp điểm
yx
0
'( ) 6
0,25
xx
2
00
3 2 1 6
x
xx x
0
2
00
0
1
3 2 5 0 5
3

0,25
Với
x y PTTT y x
00
1 2 : 6 8
0,25
Với
x y PTTT y x
00
5 230 175
:6
3 27 27
0,25