ỦY BAN NHÂN DÂN HUYỆN AN LÃO
TRƯỜNG THCS TÂN DÂN
ĐỀ KIỂM TRA ĐÁNH GIÁ CUỐI HỌC KÌ II
NĂM HỌC 2022 - 2023
MÔN: TOÁN 7
Thời gian: 90 phút (không kể thời gian giao đề)
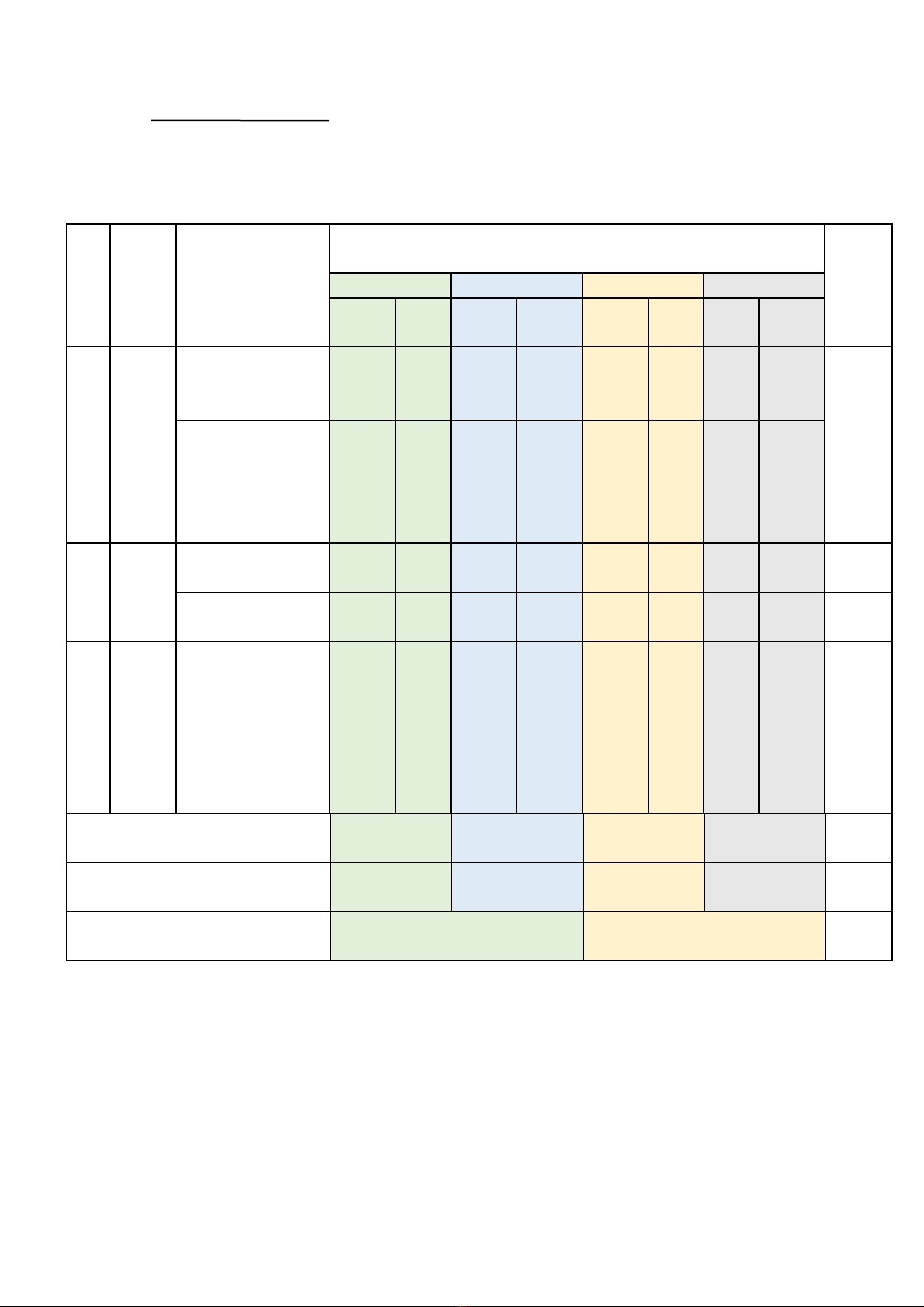
A. KHUNG MA TRÂ#N ĐÊ% KIÊ&M TRA CUÔ'I HO#C KI% 1- TOA'N 7
TT Chủ đề Nội dung/Đơn vị
kiến thức
Mư'c đô# đánh giá Tổng %
điểm
Nhâ#n biê't Thông hiê&u Vâ#n du#ng Vâ#n du#ng cao
TNK
QTL TNKQ TL TNKQ TL TNK
QTL
1
Một số
yếu tố
thống
kê và
xác
suất
Thống kê – Thu
thập và tổ chức dữ
liệu
3
0,75đ
1
0,5đ
1
0,5đ
6
(2,25)
Xác suất – Làm
quen với biến cố
ngẫu nhiên và xác
suất của biến cố
ngẫu nhiên
1
0,5đ
2
Biểu
thức
đại số
Biểu thức đại số 2
0,5đ 1
0,5đ
3
(1,0)
Đa thức một biến 3
0,75đ
1
0,5đ 2
1,0đ 1
0,5đ
7
(2,75)
3
Tam
giác
Tam giác. Tam giác
bằng nhau. Tam
giác cân. Quan hệ
giữa đường vuông
góc và đường xiên.
Các đường đồng
quy của tam giác.
4
1,0đ 2
2,0đ 1
1,0đ 7
(3,0)
Tổng 14
(4,0)
4
(3,0)
3
(2,0)
2
(1,0)
23
(10,0)
Tỉ lệ % 40% 30% 20% 10% 100%
Tỉ lệ chung 70% 30% 100%
1
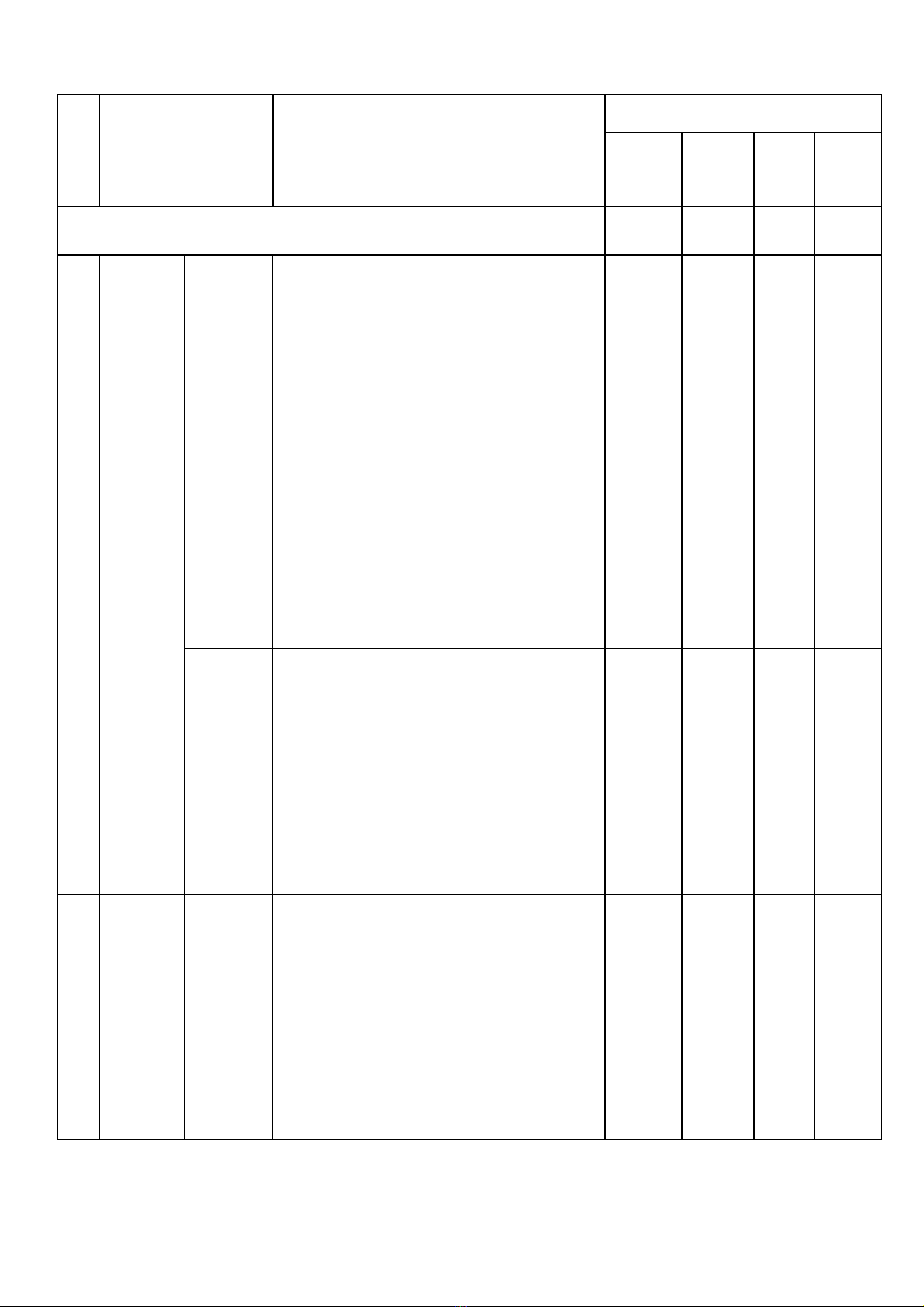
BB BẢNG ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ I, MÔN TOÁN LỚP 7
TT Chủ đề Mư'c đô# đánh giá
Số câu hỏi theo mức độ nhận thức
Nhận
biết
Thông
hiểu
Vận
dụng
Vận
dụng
cao
SÔ' VÀ ĐA#I SỐ
1
Một số
yếu tố
thống kê
và xác
suất
Thống kê –
Thu thập
và tổ chức
dữ liệu
Nhận biết:
– Nhận biết được những dạng biểu diễn
khác nhau cho một tập dữ liệu.
– Đọc và mô tả được các dữ liệu ở dạng
bảng thống kê.
Thông hiểu:
– Thực hiện và lí giải được việc thu thập,
phân loại dữ liệu theo các tiêu chí cho
trước từ những nguồn: văn bản, bảng biểu,
kiến thức trong các môn học khác và trong
thực tiễn.
– Giải thích được tính hợp lí của dữ liệu
theo các tiêu chí toán học đơn giản (ví dụ:
tính hợp lí, tính đại diện của một kết luận
trong phỏng vấn; tính hợp lí của các quảng
cáo; …)
3
(TN)
1
(TL)
1
(TL)
Xác suất
– Làm
quen với
biến cố
ngẫu
nhiên và
xác suất
của biến
cố ngẫu
nhiên
Thông hiểu:
– Tính toán được xác suất của một biến cố
ngẫu nhiên trong một số ví dụ đơn giản (ví
dụ: lấy bóng trong túi, tung xúc xắc,...).
1
(TL)
2 Biểu thức
đại số và
đa thức
Biểu
thức đại
số
Nhân biêt:
– Nhận biết được biểu thức số.
– Nhận biết được biê]u thư^c đa_i sô^.
– Xác định biến số (biến) trong một biểu
thức đại số.
– Tính được giá trị của một biểu thức đại
số.
Vận dụng cao:
– Viết một biểu thức đại số biểu thị một
mệnh đề.
2
(TN)
1
(TL)
2
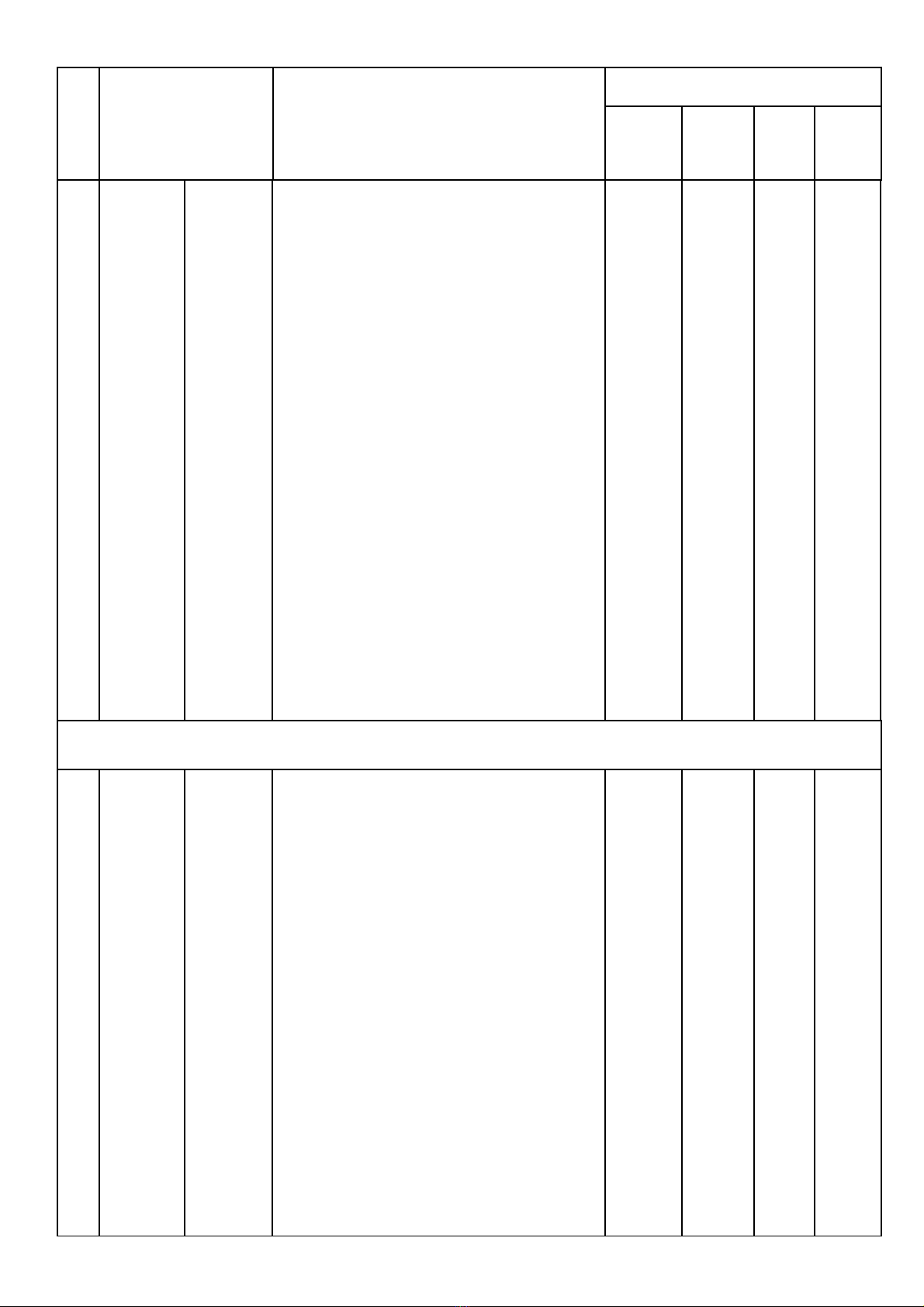
TT Chủ đề Mư'c đô# đánh giá
Số câu hỏi theo mức độ nhận thức
Nhận
biết
Thông
hiểu
Vận
dụng
Vận
dụng
cao
Đa thức
một biến
Nhân biêt:
– Nhận biết đơn thức một biến và bậc của
đơn thức.
– Nhận biết đa thức một biến và các hạng
tử của nó.
– Nhận biết bậc, hệ số cao nhất, hệ số tự
do của đa thức một biến.
– Nhận biết được nghiệm của đa thức một
biến.
– Thu gọn và sắp xếp các hạng tử của một
đa thức.
Vân dung:
– Thực hiện được các phép tính: phép
cộng, phép trừ phép nhân, phép chia trong
tập hợp các đa thức một biến; vâ_n dụng
được những tính chất của các phép tính đó
trong tính toán.
Vận dụng cao:
– Xác định được hệ số của đa thức một
biến để đa thức thỏa mãn yêu cầu.
– Vận dụng tính chất của phép chia đa thức
một biến để giải toán.
3
(TN)
1 (TL)
2
(TL)
1
(TL)
HI%NH HO#C
3Quan hệ
giữa các
yếu tố
trong một
tam giác
Tam
giác.
Tam
giác
bằng
nhau.
Tam
giác cân.
Quan hệ
giữa
đường
vuông
góc và
đường
xiên.
Các
đường
đồng quy
của tam
Nhận biết:
– Nhâ_n biê^t liên hệ về độ dài của ba cạnh
trong một tam gia^c.
– Nhận biết được khái niệm hai tam giác
bằng nhau.
– Nhận biết tam giác cân.
– Nhâ_n biê^t đường vuông góc và đường
xiên; khoảng cách từ một điểm đến một
đường thẳng.
– Nhận biết đường trung trực của một đoạn
thẳng và tính chất cơ bản của đường trung
trực.
– Nhâ_n biê^t ca^c đươjng đă_c biê_t trong tam
gia^c (đươjng trung tuyê^n, đươjng cao,
đươjng phân gia^c, đươjng trung trư_c); sự
đồng quy của các đường đặc biệt đó.
Thông hiểu:
– Giải thích được định lí về tổng các góc
trong một tam giác bằng 180°.
4
(TN)
2
(TL)
1
(TL)
3
TT Chủ đề Mư'c đô# đánh giá
Số câu hỏi theo mức độ nhận thức
Nhận
biết
Thông
hiểu
Vận
dụng
Vận
dụng
cao
giác – Tính số đo của một góc dựa vào định lí
tổng ba góc của một tam giác.
– Giải thích được ca^c trươjng hơ_p băjng
nhau cu]a hai tam gia^c, của hai tam giác
vuông.
– Mô tả đươ_c tam gia^c cân vaj giải thích
được ti^nh châ^t cu]a tam gia^c cân.
– Giải thích được quan hệ giữa đường
vuông góc và đường xiên dựa trên mối
quan hệ giữa cạnh và góc đối trong tam
giác (đối diện với góc lớn hơn là cạnh lớn
hơn và ngược lại).
– Giải thích, mô tả tính chất của các đường
đặc biệt và sự đồng quy của các đường đặc
biệt đó trong tam giác (đươjng trung tuyê^n,
đươjng cao, đươjng phân gia^c, đươjng trung
trư_c).
Vận dụng:
– Diễn đạt được lâ_p luâ_n vaj chư^ng minh
hijnh ho_c trong nhưpng trươjng hơ_p đơn gia]n
(ví dụ: lập luận và chứng minh được các
đoạn thẳng bằng nhau, các góc bằng nhau
từ các điều kiện ban đầu liên quan đến tam
giác,...).
– Giải quyết được một số vấn đề thực
tiễn (đơn giản, quen thuộc) liên quan đến
ứng dụng của hình học như: đo, vẽ, ta_o
dư_ng các hình đã học.
Tổng số câu 14 4 3 2
Tỉ lệ % 40% 30% 20% 10%
Tỉ lệ chung 70% 30%
4
PHẦN I. TRẮC NGHIỆM( 3 điểm).
Hãy khoanh tròn chỉ một chữ cái đứng trước phương án trả lời đúng.
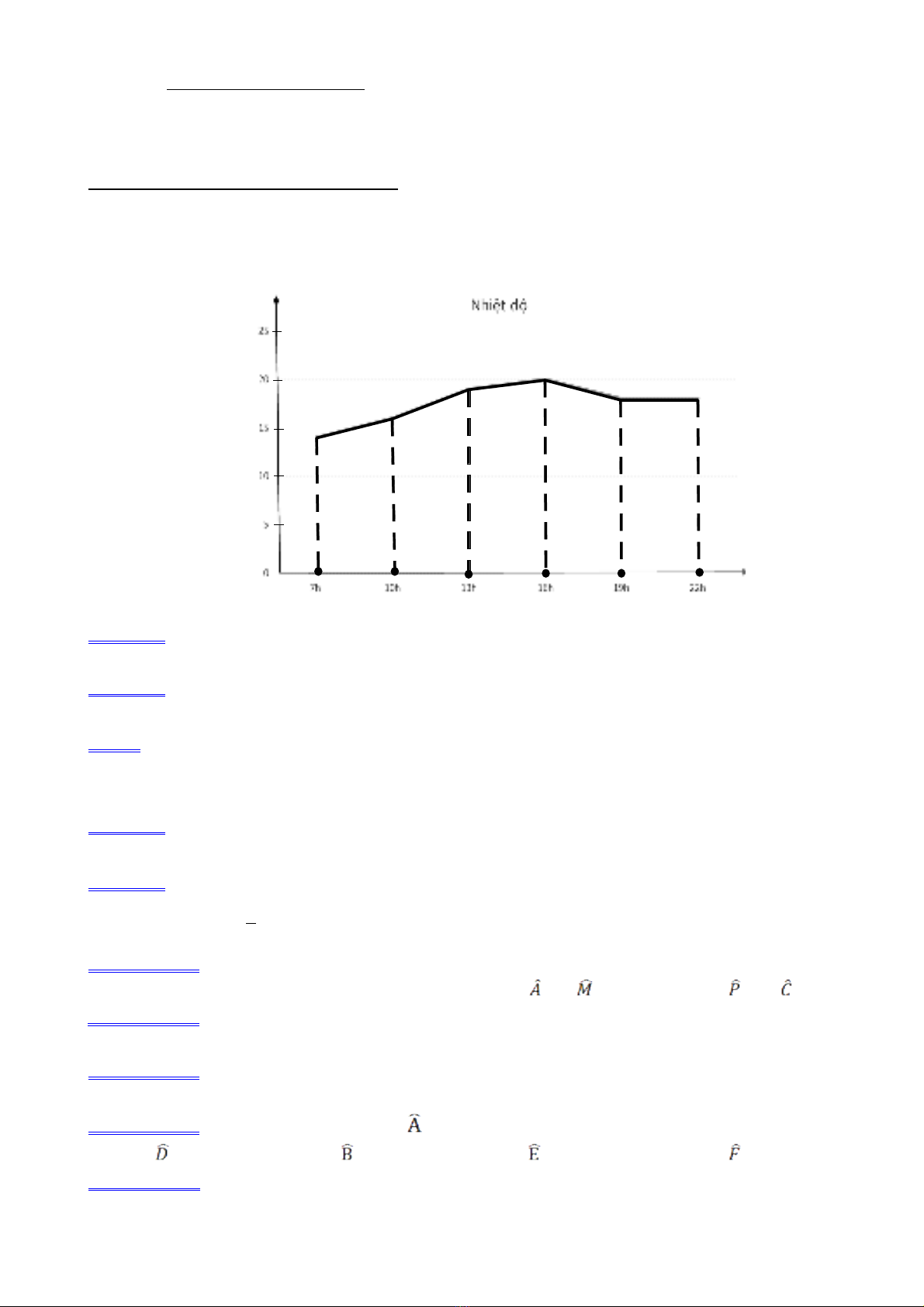
Dựa vào biểu đồ đoạn thẳng ở hình bên biểu diễn nhiệt độ ở thành phố A được cập nhật trong
ngày. Trả lời câu hỏi từ câu 1 đến câu 3.
Câu 1: Cho biết nhiệt độ ổn định trong khoảng thời gian nào ?
A.7h - 10h. B.13h - 16h. C.19h - 22h. D.10h - 13h.
Câu 2: Cho biết nhiệt độ lúc 16h ?
A.
0
20 C
. B.
0
19 .C
C.
0
16 C
. D.
0
14 C
.
Câu 3: Biết chênh lệch nhiệt độ trong ngày bằng hiệu của nhiệt độ cao nhất và nhiệt độ thấp
nhất ngày hôm đó. Vậy chênh lệch nhiệt độ của ngày hôm đó ở thành phố A là bao nhiêu ?
A.
0
20 C
.B.
0
15 C
. C.
0
10 C
D.
0
6C
.
Câu 4: Cho đa thức
4 3 2
4 3 1A x x x x
= − + − +
.Giá trị của A tại x = -2 là :
A.
35A
= −
. B.
53A
=
. C.
33A
=
. D.
35A
=
.
Câu 5: Kết quả của phép chia
là :
A.
4 2
1
3 2 3
x x+ −
. B.
8 2
3x 2 x 3x
+ −
. C.
6 4
3x 2 x x
+ +
. D.
3 2
9 x 2 x x
− −
.
Câu 6: Cho
ABC MNP
∆ = ∆
. Chọn câu sai :
A. AB = MN. B. AC = NP. C. = . D. = .
Câu 7: Bậc của đa thức
6 3 2
3 2x x x
+ −
là :
A. bậc 3 . B. bậc 4. C. bậc 5 . D. bậc 6.
Câu 8: Kết quả của phép tính 9x + 7x là :
A. 16x B. 63x C.16x
2
D. 63x
2
Câu 9: Cho
ABC DEF
∆ = ∆
. Biết =
0
50
. Khi đó:
A. =
0
50
. B. =
0
50
. C. =
0
50
.D. =
0
50
Câu 10: Nhận xét nào dưới đây sai?
A. Ba đường phân giác của một tam giác cùng đi qua một điểm;
5
ỦY BAN NHÂN DÂN HUYỆN AN LÃO
TRƯỜNG THCS TÂN DÂN
ĐỀ KIỂM TRA ĐÁNH GIÁ CUỐI HỌC KÌ II
Năm học 2022 – 2023
Môn: Toán 7
Thời gian: 90 phút
(Không kể thời gian giao đề)
18
0
C
18
0
C
20
0
C
19
0
C
16
0
C
14
0
C
Thời gian
Nhiệt độ
0
C