ÑEÀ THI HOÏC KYØ 2 MOÂN TOAÙN
Ñeà 1
THÔØI GIAN LAØM BAØI : 90 PHUÙT
GIAÙO VIEÂN RA ÑEÀ : ÑINH VAÊN TRÍ
Caâu 1
Giaûi baát phöông trình :
( )
1 3 3
2 2 2x 1 x 1
+ £
- + .
Caâu 2
Tìm taát caû caùc giaù trò cuûa tham soá m ñeå baát phöông trình 2 2
3x 2 2 mx m 2m 3 0 - + - + > coù taäp
nghieäm laø R.
Caâu 3
Giaûi heä baát phöông trình : 2
x 2 0
1 x
x 2x 0
+
ì £
ï - +
í
ï + ³
î
.
Caâu 4
Chöùng minh raèng : cos7x.cos5x +sin4x.sin8x = cos3x.cosx.
Caâu 5
Cho 5
cosa 13
= - vaø 3
a 2
p
p < < .Tính cos 2a
2
p
æ ö
-
ç ÷
è ø .
Caâu 6
Tính giaù trò cuûa bieåu thöùc 2
cos2x 1
A sin x sin2x
1 tan x 2
= + +
+ .
Caâu 7
Cho tam giaùc ABC coù caïnh a = 28 , caïnh b = 12 vaø c = 20.
a)Tính goùc A cuûa tam giaùc ABC.
b)Tính ñoä daøi ñöôøng cao haï töø ñænh B cuûa tam giaùc ABC.
Caâu 8
Trong maët phaúng toa ñoä Oxy cho tam giaùc ABC ,bieát A(-2;5), B(-4;1), C(1;2).
a)Vieát phöông trình toång quaùt cuûa ñöôøng cao BH vaø phöông trình tham soá cuûa ñöôøng trung
tuyeán CM.
b)Vieát phöông trình ñöôøng troøn taâm A vaø tieáp xuùc vôùi ñöôøng thaúng BC.
Heát.
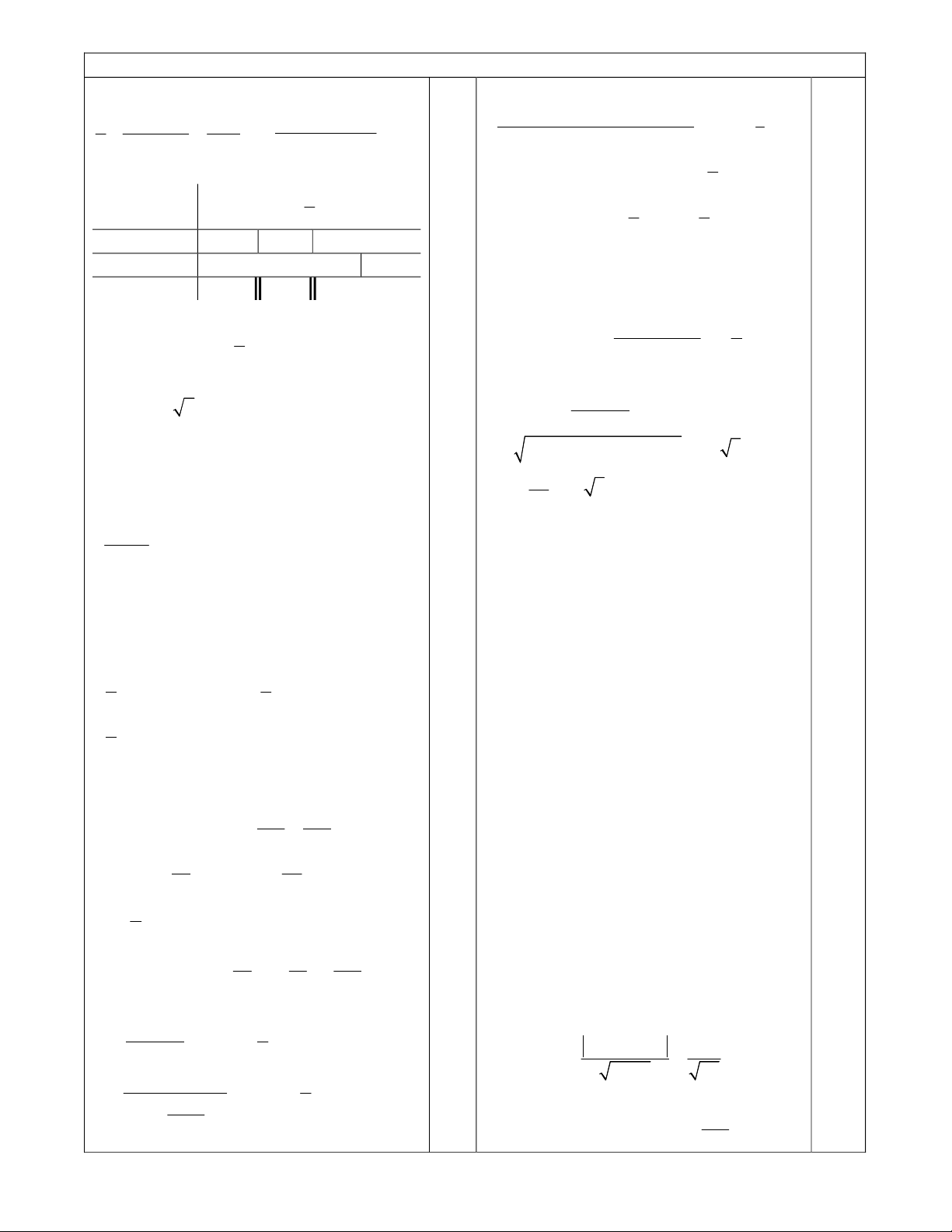
Ñaùp aùn ñeà 1
Caâu 1 (1 ñieåm)
( )
1 3 3
2 2 2x 1 x 1
+ £
- + Û
( )
( )( )
2
x 2 0
2x1x1
- £
- +
Baûng xeùt daáu
x -¥ -1 1
2 2 +¥
(x-2)
2 + + + 0 +
(2x-1)(x+1) + 0 - 0 + +
Veá traùi + - + 0 +
Keát luaän : 1
1 x hay x 2
2
- < < =
Caâu 2 ( 1,0 ñieåm )
2 2
3x 2 2 mx m 2m 3 0 - + - + > , x R " Î
Û D < 0
Û 2
4m 24m 36 0 - + - <
Û " m ¹3
Caâu 3 ( 1,0 ñieåm )
2
x 2 0
1 x
x 2x 0
+
ì £
ï - +
í
ï + ³
î
Û 2 x 1
x 2 hay x 0
- £ <
ì
í £ - ³
î
Ûx = -2 hay 0 £ x <1
Caâu 4( 1,0 ñieåm )
cos7x.cos5x +sin4x.sin8x
=
( ) ( )
1 1
cos2x cos12x cos 4x cos12x
2 2
+ + -
=
( )
1 cos2x cos4x
2 +
=cos3x.cosx.
Caâu 5( 1,0 ñieåm )
2 2 25 144
sin a 1 cos a 1 169 169
= - = - =
Þ sina= - 12
13 ( vì 3
a 2
p
p < < )
cos 2a
2
p
æ ö
-
ç ÷
è ø = sin2a = 2sina.cosa
= 12 5 120
2. .
13 13 169
æ ö æ ö
- - =
ç ÷ ç ÷
è ø è ø
Caâu 6 ( 1,0 ñieåm )
2
cos2x 1
A sin x sin2x
1 tan x 2
= + +
+
= 2 2 2
cos x sin x 1
sin x sin2x
sinx 2
1 cosx
- + +
+
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,5
0,5
0,25
0,25
0,25
0,25
0,25
0,25
0,25
=
( )( )
2
cosx sinx cosx sinx cosx 1
sin x sin2x
cosx sinx 2
- + + +
+
( )
2 1
cosx sinx cosx sin x sin2x
2
= - + +
=
( )
2 2 1 1
cos x sin x sin2x sin2x
2 2
+ - +
=1
Caâu 7 ( 1,5 ñieåm )
caïnh a = 28 , caïnh b = 12 vaø c = 20.
a)Ta coù : 2 2 2
b c a 1
cosA 2bc 2
+ -
= = -
Þ
µ
0
A 120 =
b) Ta coù :p a b c 30
2
+ + = .
( )( )( )
S p p a p b p c = - - - =60 3 .
b 2S
h 10 3
b
= = .
Caâu 8 ( 2,5 ñieåm )
Bieát A(-2;5), B(-4;1), C(1;2).
a)Ta coù : BH ^ AC
Þ ñöôøng thaúng BH coù vectô phaùp tuyeán laø
( ) ( )
AC 3; 3 3 1; 1 = - = -
uuur
Þphöông trình toång quaùt cuûa ñöôøng thaúng
BH coù daïng : x – y + C0 = 0 .
Ñöôøng thaúng BH ñi qua B Þ C0 = 5
Vaäy phöông trình toång quaùt cuûa ñöôøng
thaúng BH laø : x – y + 5 = 0.
Ñieåm M laø trung ñieåm caïnh AB ÞM(-3;3)
Ñöôøng thaúng CM coù vectô chæ phöông laø
( )
CM 4;1 = -
uuuur .
Phöông trình tham soá cuûa ñöôøng thaúng CM
x 1 4t
y 2 t
= -
ì
í = +
î (t ÎR)
b)
( )
BC 5;1 =
uuur
Ñöôøng thaúng BC coù vectô phaùp tuyeán laø
( )
n 1; 5 = -
r
Phöông trình ñöôøng thaúng BC : x – 5y +9=0
Baùn kính cuûa ñöôøng troøn caàn tìm :
R=d(A,BC)= 2 5.5 9 18
1 25 26
- - + =
+
Phöông trình ñöôøng troøn caàn tìm :
(x+2)
2 + (y – 5 )
2 = 162
13
0,25
0,25
0,25
0,5
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
Heát.
ÑEÀ THI HOÏC KYØ 2 MOÂN TOAÙN
Ñeà 2
THÔØI GIAN LAØM BAØI : 90 PHUÙT
GIAÙO VIEÂN RA ÑEÀ : ÑINH VAÊN TRÍ
Caâu 1
Giaûi baát phöông trình :2 2
3 2 2 3
4 2
x x
x x x
- -
£
- - .
Caâu 2
Tìm taát caû caùc giaù trò cuûa tham soá m ñeå haøm soá
( )
2 2 2
2 4 1 1 2y x m x m = + - - + coù taäp xaùc ñònh
laø R.
Caâu 3
Cho tam giaùc ABC .Tính giaù trò cuûa bieåu thöùc2 2
sin sin cot .cot
2 2 2 2
+ +
= + +
A B C B A C
P .
Caâu 4
Chöùng minh raèng : cosa + cosb + cosc + cos(a+b+c) = + + +
4cos cos cos
2 2 2
a b b c c a .
Caâu 5
Cho 3
sina 5
= - vaø 3
a 2
p
p < < .Tính sin4a.
Caâu 6
Ruùt goïn bieåu thöùc 3 3
2010cos x 2009cos3x 2010sin x 2009sin3x
A cos x sin x
- +
= + .
Caâu 7
Trong tam giaùc ABC coù ba caïnh a, b, c thoûa heä thöùc :2 2 2
17 9 4 24 4 a b c ab ac + + = + .Tính cosA.
Caâu 8
Trong maët phaúng toa ñoä Oxy cho tam giaùc ABC ,bieát A(-2;5), B(-4;1), C(1;2).Vieát phöông trình
ñöôøng troøn ngoaïi tieáp tam giaùc ABC.
Caâu 9 :
Trong maët phaúng toa ñoä Oxy cho 2 ñieåm A(-6 ; 5) , B( 4 ; 1) .Vieát phöông trình toång quaùt cuûa
ñöôøng thaúng laø trung tröïc cuûa ñoaïn AB.
Caâu 10 :
Trong maët phaúng toa ñoä Oxy cho ñöôøng troøn (C) coù phöông trình :2 2 4 6 7 0 x y x y + + - - = .Vieát
phöông trình tieáp tuyeán cuûa ñöôøng troøn (C), bieát tieáp tuyeán song song vôùi ñöôøng thaúng d coù phöông trình
:x -2y + 18 = 0 .
Heát.
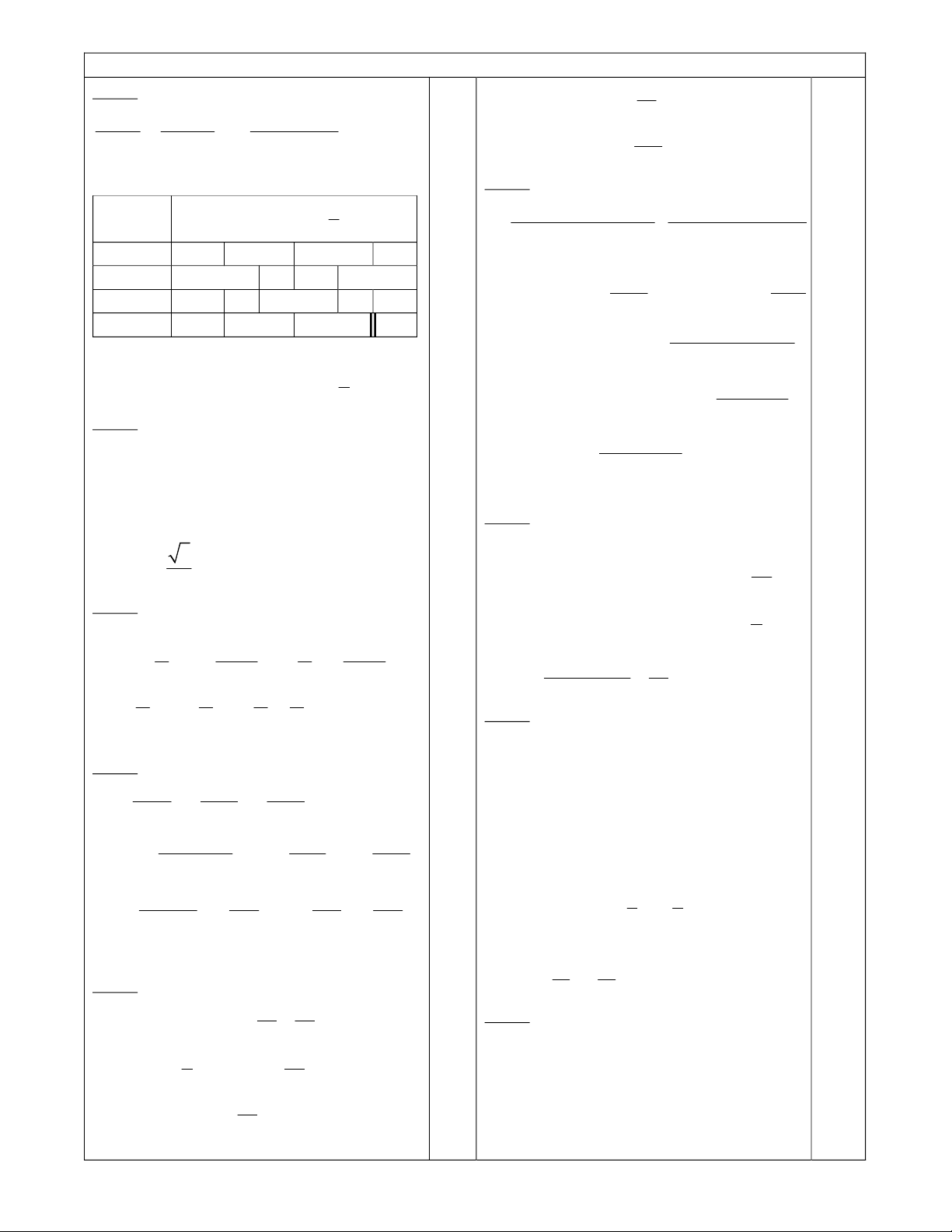
Ñaùp aùn ñeà 2
Caâu 1 (1 ñieåm)
2 2
3 2 2 3
4 2
x x
x x x
- -
£
- - Û
( )
2
2
5x x 6 0
x x 4
- + + £
-
Baûng xeùt daáu
x -¥ -2 -1 06
5 2 + ¥
2
5 6
x x - + + - - 0 + + 0 - -
2 4x - + 0 - - - - 0 +
x - - - 0 + + +
VT + - 0 + - 0 + -
Keát luaän : 6
2 x 1 hay 0 x hayx 2
5
- < £ - < £ >
Caâu 2 ( 1,0 ñieåm )
Haøm soá coù taäp xaùc ñònh laø R
Û
( )
2 2 2
2 4 1 1 2 0x m x m + - - + ³ , x R " Î
Û D £ 0
Û 4 2
16m 24m 9 0 - + £
Ûm3
2
= ±
Caâu 3 ( 1,0 ñieåm )
Trong tam giaùc ABC, ta coù : A+B+C = π
2 2
sin sin cot .cot
2 2 2 2
+ +
= + +
A B C B A C
P
=2 2
sin cos . .
2 2 2 2
+ +
A A B B
cot tg
= 1 + 1 = 2
Caâu 4 ( 1,0 ñieåm )
+ + +
4cos cos cos
2 2 2
a b b c c a
= æ ö
æ ö æ ö æ ö
+ + - +
÷
ç ÷ ÷ ÷
ç ç ç
÷
÷ ÷ ÷ +
ç ç ç ç
÷
÷ ÷ ÷
ç ç ç ç
÷ ÷ ÷
ç ç ç ÷
ç è ø è ø è ø
è ø
2
2 cos cos cos
2 2 2
a b c a c c a
= æ ö æ ö æ ö æ ö
+ + + - +
÷ ÷ ÷ ÷
ç ç ç ç
÷ ÷ ÷ ÷
+
ç ç ç ç
÷ ÷ ÷ ÷
ç ç ç ç
÷ ÷ ÷ ÷
ç ç ç ç
è ø è ø è ø è ø
2
2cos cos 2cos cos
2 2 2 2
a b c c a a c c a
=
( )
+ + + + + cos cos cos cos a b c b a c(ÑPCM)
Caâu 5 ( 1,0 ñieåm )
2 2 9 16
cos a 1 sin a 1 25 25
= - = - =
Þ 4
cosa 5
= - ( vì 3
a 2
p
p < < )
sin2a = 2sinacosa=24
25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,5
0,25
0,25
0,5
0,25
0,25
0,25
cos2a=2 7
1 2 sin
25
a - =
sin4a=2sin2acos2a=336
625
Caâu 6 ( 1,0 ñieåm )
3 3
2010cos x 2009cos3x 2010sin x 2009sin3x
A cosx sinx
- +
= +
2 2
cos3x sin3x
2010cos x 2009 2010sin x 2009
cosx sinx
= - + +
2 2 sin3xcosx cos3xsinx
2010cos x 2010sin x 2009 sinxcosx
æ ö
-
= + + ç ÷
è ø
( )
2 2 sin2x
2010 cos x sin x 2009 cosxsin x
æ ö
= + + ç ÷
è ø
2cosxsin x
2010 2009 cosxsinx
2010 2009.2 6028
æ ö
= + ç ÷
è ø
= + =
Caâu 7 ( 1,0 ñieåm )
Ta coù :2 2 2
17 9 4 24 4 a b c ab ac + + = +
( ) ( )
2 2
4
3
4 3 2 0
2
ì =
ï
ï
Û - + - = Û í
ï =
ï
î
a
b
a b a c a
c
2 2 2
b c a 37
cosA 2bc 48
+ -
= = .
Caâu 8 ( 1,0 ñieåm )
Goïi phöông trình ñöôøng troøn (C ) coù daïng:
2 2 2 2 0 x y ax by c + - - + =
Bieát A(-2;5), B(-4;1), C(1;2) naèm treân ( C)
Ta coù heä :
4 10 29
8 2 17
2 4 5
a b c
a b c
a b c
ì - + = -
ï - + = -
í
ï
- - + = -
î
Ta tìm ñöôïc :5 7 1
3 3
, ; a b c = - = =
Phöông trình (C ) caàn tìm :
2 2 10 14 1 0
3 3
x y x y + + - + =
Caâu 9 ( 1,0 ñieåm )
Goïi d laø ñöôøng thaúng trung tröïc cuûa ñoaïn
AB Þ d vuoâng goùc vôùi ñoaïn AB taïi
( )
1 3 ; I - laø trung ñieåm ñoaïn AB.
D coù VTPT
( ) ( )
10 4 2 5 2 ; ; AB = - = -
uuur
Pt ñt d coù daïng : 5x – 2y + C0 = 0
0,25
0,25
0,25
0,25
0,25
0,25
0,5
0,5
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
I Î d Þ C0 = 11
KL : Phöông trình d : 5x – 2y + 11 = 0
Caâu 10 ( 1,0 ñieåm )
Goïi D laø tieáp tuyeán cuûa (C) vaø D song
song vôùi d Þ D:x – 2y + c = 0 ( ÑK:c ¹0)
(C) coù taâm I(-2 ;3) vaø coù baùn kính R = 20
D laø tieáp tuyeán cuûa (C) Ûd(I, D) = R
Û
8
20
5
c - + = Û8 10
8 10
c
c
é- + =
ê
- + = -
ë
Û18
2
(Loaïi)
(Nhaän)
c
c
é =
ê = -
ë
KL : Phöông trình d : x – 2y -2 = 0
0,25
0,25
0,25
0,25
Heát.