
so GrAo DUC VA EAOTAO HA NQr
rnr-IoI.rc TIIPT CHU vAfq AN
{*.-
ne rlrt THU DAr Hec EOTTr NAvr zor r
MOn Toin - fndi A
Thdi gian ldm bdi: 180 phft, kh0ng td ttrOi gian giao d0.
OA ttri g6m 01 trang.
PHAN cIruNG (z iti6m)
B il (2 drd@.Cho hdm s5 y = ?4
x-l
i. Kh6o s6t vd vc dd thi cria hdm s6 da cho.
. 2. Gei r ra giao di6m't;ft;o't;;;e*;; cria r10 th!. rim di6m M tr€n d0 thi sao cho ti6p
tuy€n tgi M wdng g6c vdi IM.
Bii u (2 diam) lx-alvl+3 = 0
l. Giai hQ phuong trinh: ] - "'
[!/lo&,<-./iog,y=o'
2. Giaiphuong trinh, sit 2* n t-9t t* = tan x - cot x .
cosx smx
Bii III (1 die@. Tim th6 tfch kh6i trdn xoay dugc tpo thanh khi quay quanh t4rc Ox hinh ph8ng
gidi han bOi dd thi (C) cta hdm s5 y = *dt([*) vd ciic cfudrng thing y = 0, x = 1.
Bei W ( did@. Cho hinh ch6p S.ABC c6 d6y ld tam gi6c cAn (B = e - o)- C6c rludng thing SA,
SB, SC tpo vdi m[t phfrng ddy cdc g6c b].ng nhau. Ggi V, ua V, lAn luqt la th0 tfch cria hinh ch6p
vd th6 tich hinh n6n ngo4i tii5p hinh ch6p. Tinh theo cr ,y ,6 $.
'v2
(.
lxr+x+log21=8Y'+2Y+1
Bni V Q diA@. Giei he phuong trinh: ] Y
lu'-ro+1=o (vdix> o' Y> o)'
L" "4
PHAN fV CHQN Q itid@. Thi sinh )nt "npo mQt trong hai phb): Phdn A ho(e Phdn B.
Phin A:
Bii VIa Q diiim)
l. Trong mflt phEng tga ilQ Oxy, cho tluong trdn {C): (x-1)' +(y +2)2 =9 vd dutrng thing
(d):3x-4y+m=0.Timmd6tr6n(d)c6duynhfltdiOmPsaochotrlPc6thekedugchaiti6p
tuy6n PA, PB vdi dudng trdn vd tam gi6c PAB la 6m gi6c vudng (A, B ld cdcti€p diem).
2.Chohai ducrngth$ng d'*--1= yr 1 =t ^l vd A: x-2 = y, 3 =t --4 trongkhdng
212123
gian v6i hQ to4 dQ Oxyz. Bi6t rang d vd Acft nhau. HEy vi6t phuong trinh mf,t phing (P) chrla A
sao cho g6c gita dulng th6ng d vd m6t phing (P) l6n nh6t.
Bii YIIa (I di6m). Gi6i phuong trinh: 9x + 2(x - 2).3" + 2x - 5 = 0.
PhAn B:
Bni vlb (2 die@
1. Trong mlt ph&ng tqa dQ Oxy, cho dudng trdn (C): (x - l)t + (y + l)'? - 25 , diiSm M(7; 3).
Vi6t phucrng trinh ttuhng th&ng qua M c6t (C) tai hai di6m phAn biQt A, B sao cho MA = 3MB.
2. Tt cdc cht sd 2, 3, 4, 7, 8, g c6 th6 lflp tluqo. bao nhi€u si5 tu nhien 16 c6 s6u cht s6, trong
d6c6dungbachfr s6ZZ
BAi VIIb ( diim).Gi6i phuong trinh tr€n tflp ttsp f5 phttc: za - z3 + 6* - 8z - 16= 0.
HCt --------------
Hq vdtOnth{ sinh: .......,.. ..S6 Oao Oanh:
jimca97@yahoo.com sent to www.laisac.page.tl

Hr-l5Nc nAN cnA,r vn nrdu odu udx roAN - rsdl a
nnl u6r nuNc DIEM
BEi I
2d CAU L (1.25 ttiim)
a)TXD:x*1 0.25
b) Sg bi6n thi€n:
+ Nh6nh v6 cqc vd duirng tiOm cAn:
Iim y=2' lim y= 2:'Dd thi c6 tigm cQnngang y =),
x-)-00 x-)+co
lim y =-oo; lim y - .o: Dd thi c6 tiQm cAn drfurg x = 1
x-+I x-+l'
o,25
_1
+ Yt=--: ^ "
' (x -l)'
+ Bing bidn thit
F-
lY'
< 0,Vx * 1, do d6 hhm sd nghich bidn uOn (-co;
in
-oo 1 *co
I_
I
vd (1; +oo)
0,25
2
fco
+co
)
c) Dd thi:
Dd thicSt ox r?i didm A( j, ol,
c6tOy tai B(0, 1)
VE dfng, dep
0,50
Chu2 (0,75 ilidm)
Ta c61(L;2). Gi6 srt M(xo, yo), ta c6 hQ sd g6c ctra IM lb k = Y o -2 = --l - .
xo-1 (*o-1)t' 4,25
Tidp tuydn tai M vu0ng g6c vdi IM khi vd chi khi k.y'(x6) = -1
-1 1
e;---:r .--J= -1<> (xs -1)a = 1
(xo -l)' (xo -1)
o,25
TU d6 ta duoc M(2: 3) hodc M(0:1) a"25
Bni u
2d cau l, (1ili6m)
+ Didu kiQn x > 1, y ) 1. L{p ludn dua vd hg: [*-0, +3:0
[loga x =logzy 0.50
i*-ay+3=0
<+1 r
Ix=y" 0.25
+ GiAi ra c6 nshiOm (1: 1): (9: 3). o.25
Cilr2 (1diim)
+ Didu kion x *nL
'2 4,25
a-
+ Giai (2) ta duo.c *= * *k! no4c x = n +kLn
-tJ
_0al
o,25

+ Kgt hqp didu kiQn ta dugc x =tt+kZn 0,25
B}i IU
1-.I + LAp luan ra dugc y = *1G(i + *) khdng 0m tr6n tdp xdcdinh 11 [O;+*) ;0,25
I
+ Ldp luan ra duo. c thd r(ch ld v = n Ix2 h(l + x3)dx
0
0,25
+ Dung cong thrlc rich ph&n tungphdn dd bidn ddi tfch ph6n I = I*'h(l+ x3)dx :
0
l=4.m6**rlll -'r4.Ai d* =tn2-ti ,.t o'.
3 '10 d3l+xr 3 jl+xi
0,25
+rrnh dusc tichphan J= J** = i[.' *jd"
1-1rn z.ydvrhdrichcdntimld v= tr(21n2*r) .
33 3
=d-.!,nrt**rill
3 3 ',10 0,25
Bni w
1d + Ggi H ld chAn ducrng cao cta ch6p, chrlng minh duoc H ld tam duong trdn ngo?i
1!{p tamgi6c ABC. 0,25
+ Dat AB = AC = a; Tinh dugc dign tich tam gi6c ABC li, S, = 1a'sin2a;
2
0,25
+ Tinh dugc diQn tfch hinh trdn ngoai tiOp tam gidc ABC ld S, na'
=-
4sin2 s,
0,25
+Y _ SH.q/3 _ S, _
v2 sH.s2 /3 s2
4sin3 acosa o,25
Bni v
1d +(1) e x3 +x+ log, x -log, y = 8y' +2y+1
<+ x3 + x + log, x = (2y)' +2y +logr(2y) (q) 4,25
+ L4p lufln duo. c hbm sd f(t) = t3 + t + 1og2 t ddng bion tren (0;+oo) 0,25
+ Do d6 (3) <+ x=2y. 4,25
+ Thd x = 2y vio (2) vb kdt hqp didu ki0n ta duo.c nghi€m * = l,y = 1.
2o,25
Bii VIa
2d cau I (l rtidm)
+ Dudrng trbn d6 cho c6 Am I(L;1\, b6n kinh R = 3 ;0,25
+ Tam gi6c PAB luOn cAn tai P, do d6 ndu n6 wOng thi wdng t+i P; Khi dd trl
ei6c PAIB lb hinh vu0ns canh 3 vh do d6 PI = 3Ji 0,25
t*D€ t$l t+i duy nhdt didm P thi khotrng cdch tt I den (d) bing 3J2 4,25
lm+81
+ Trlc g Jil--J =3J2; GiAi ra ta duoc m = *8 xlsJt
5
0,25
cku? (1 tlicm)
r.Fgr{s"-q"--c-.eis-e-*".-qgr.q.r+s--4":s"A..l*"-M0;1-;"0-
; Ldt;:t5;tfi;rilaCa;cal"ifid"Klan dqr ie ** *-; -*t***-
hinh chidu cria A trcn (P) vd A. Ta c6 y
AH < AK suy ra lAlvftI< IAMK, ding , ','l , = ,
thrlc xAy ra khi vi chi khi H trung K, trlc li - / -r- / I Q/
AKI(P). / -.' / lr /
Nhu vay g6c gifia d vd @) lon nh6t khi / -.t I L1 /
vhchikhiAKJ-(P)t4iK. /ffi*r\
0,25
4,25
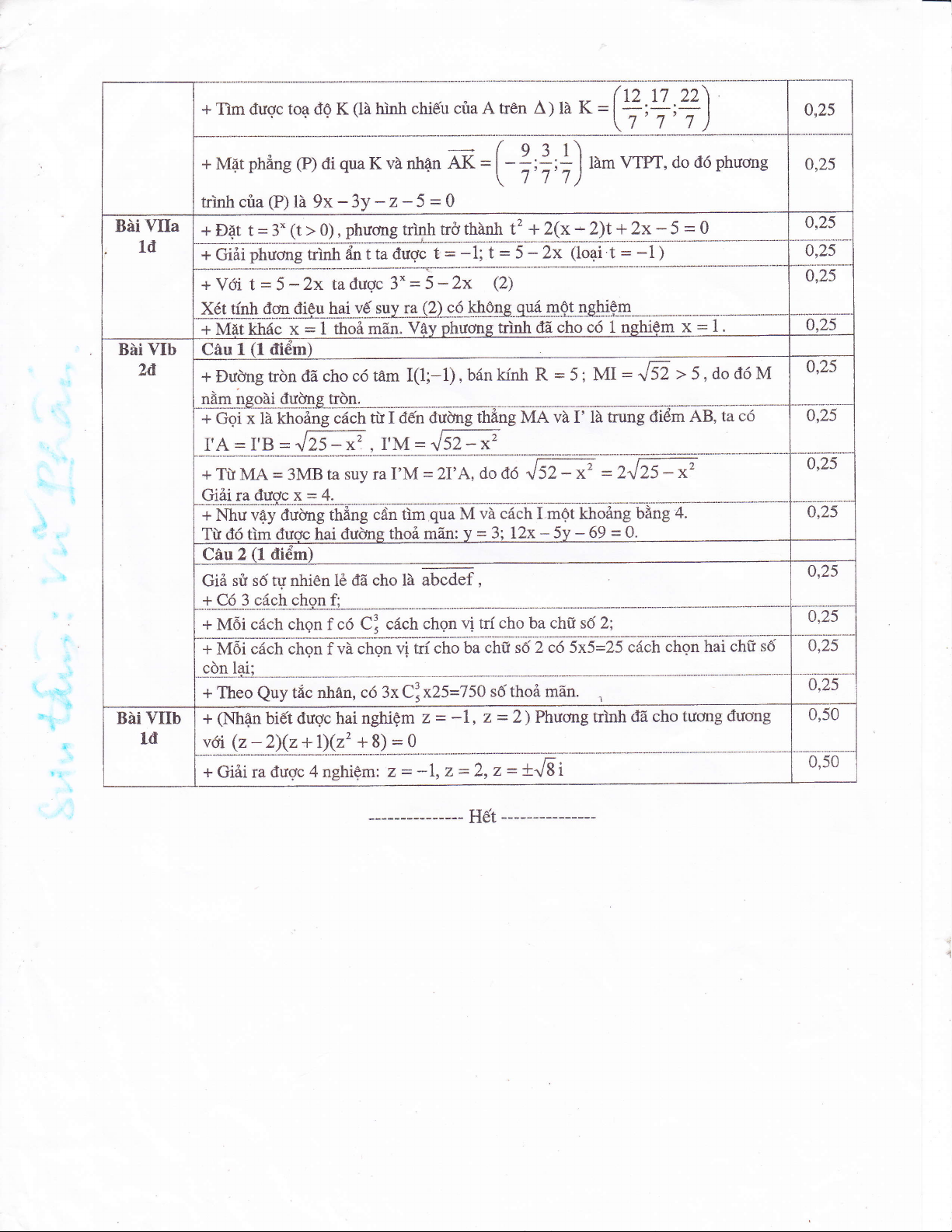
+ Tim duo.c toa dQ K (h hinh chieu ciia A tr€n A) h K =(*ry-,?\
.rvrrA)LqLr -[Zr 7t 7 )0,25
+ Mar phing (p) di qua K vd nhan AR = f-:t:,:l ldm vrPr, do d6 phuong
\. 7'7'7 )
trinh cria @) li 9x -3y - z - 5 = 0
4,25
Bii YIIa
kl + DAt t = 3" (t > 0), phuong trinh fiA thenh tz + 2(x *2)t +2x - 5 = 00,25
+ GiAiphuong trinh dnttadud.c t= -l; t = 5 -2x (1o4i t = -1) 0,25
+Vdi t = 5-2x tadugc 3* =5*2x (2)
X6t tfnh don diOu hai vd suv ra (2\ cd khOne qu6 m6t nshiOm
a,25
+ Mft kh6c x = 1 thoi mdn. VOy phuong trinh de cho c6 1 nghi€m x =-1-:- 0,25
Bii vlb
2d Ceu 1 (1 rliim)
+ Dudng trbn dd cho c6 am I(1;-1), b6n kinh R = 5; MI = Jn ,5, do d6 M
nf,m neodi dulne trbn.
Q,25
;Ceil Ie kh'A"s;a;,l';ti dsnA;dns;hAns MCil irittruns cidm An, ta co
I,A : I'B = fr5-;, I,M = J52 -7 o,25
+ Tt MA = 3MB ta suy ra I'M = 2I'A, do d6
Giiiraduo.cx=4.
0,25
; Nhtvat dnhnt ih&ng cdn tim qua M vb c6ch I-mQt khoAng bing 4.
TU d6 tim duoc hai duirne thoi m6.n: y = 3; LZx - 5y - 69 = 0.
a.25
Chu2 (l tliim)
Gi6 st sei tu nhicn 16 d5 cho ld abcdef ,
+ C6 3 cdch chqn f;
o,25
+ M6i c6ch chgn f c6 Cl c6ch chon vi tri cho ba cht sd 2; a,25
+ M6i c6ch chqn f vh chgn vi trf cho ba chfi sd 2 c6 5x5=25 c6ch cho:t hai cht sd
cbn lai:
0,25
+ Theo Quy t6c nhEn, cd 3xC3rx25=750 sd thoi mdn. ja,25
BEi VIIb
1d + (NhAn bidt duo.c hai nghi€m z = -1, z = 2) Phuong trinh di cho tudng duong
v6r (z-2)(z+I){2'?+ 8) = 0
+ Gi6i ra duoc 4 nghiom: z = -10 z = 2, z = XJS|
0,50
0;30
-- Hdt






















![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)



