…Hết…
(Cán bộ coi thi không giải thích gì thêm)
TRƯỜNG THPT
MAI ANH TUẤN
NGA SƠN _ THANH HÓA
ĐỀ THI THỬ ĐẠI HỌC LẦN II KHỐI A NĂM 2009
Môn: Toán
Thời gian làm bài 180 phút
PHẦN CHUNG CHO MỌITHÍ SINH
Câu I (2 điểm). Cho hàm số
3 2
3 ( 1) 1y x x m x
có đồ thị là (Cm)
1. Khảosátvà vẽ đồ thị hàm sốkhi m = 2.
2. Tìm những giá trị của m để đường thẳng
1y x
cắt đồ thị (Cm)tại 3 điểm phân biệt A(0; 1), B, C
sao cho các tiếp tuyếncủa (Cm)tại B và C vuông góc với nhau.
Câu II (2 điểm).
1. Giải hệ phương trình
3 3
3 3
x y
y x
2. Giải phương trình
23sin2sinsin 222 xxx
Câu III (2 điểm)
1. Tính thể tích vật thể tròn xoay sinh ra khi quay hình phẳng giớihạn bởi đường tròn tâm I(2; 2) bán
kính R = 1 quanh trụchoành.
2. Trong không gian cho hai điểm A, B cố định, độ dài đoạn AB = a > 0. Ax và By là hai nửa
đường thẳng vuông góc với nhau và cùng vuông góc với AB. Trên Ax và By lấy hai điểm M và N sao
cho MN = b (với b là một số cho trước và b > a).
a) Xác định tâm và bán kính mặt cầu ngoại tiếp tứ diện ABMN.
b) Xác định vị trí của M và N sao cho tứ diện ABMN có thể tích lớn nhất.
Câu IV (1 điểm). Tìm m để bất phương trình sau có nghiệm:
.
PHẦN TỰ CHỌN:Mỗi thí sinh chỉ chọn câu Va hoặc Vb
Câu Va (3 điểm). Chương trình cơ bản
1. Trong mặt phẳng tọa độ Oxy, cho điểm P(3; 1) và hai đường thẳng có phương trình là
1:2 1 0d x y
và
2: 2 3 0d x y
. Viết phương trình đường thẳng đi qua P và tạo với hai đường
thẳng
1 2
àd v d
một tam giác cân có đỉnh là giao điểm của
1 2
àd v d
.
2. Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
11 2 1
:2 1 1
x y z
21 2 3
:2 1 2
x y z
và mặt cầu (S): x2 + y2 + z2 + 4x -2y +6z + 5 = 0. Viết phương trình mặt
phẳng tếp xúc với mặt cầu (S) đồng thời song song với
1
và
2
.
3. Tìm phần thực của số phức
2009
1i
Câu Vb. (3 điểm). Chương trình nâng cao
1. Trong mặt phẳng tọa độ Oxy, cho elip
( )E
có phương trình
2 2 1
9 4
x y
và điểm M(- 1; 1)
Viết phương trình đường thẳng đi qua điểm M và cắt
( )E
tại hai điểm A, B sao cho M là trung điểm của
đoạn thẳng AB.
2. Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A(1; 3; - 2), B(0; 0; 1), C(2; 0; 1). Tìm tọa
độ của điểm M sao cho MA2 + MB2 + MC2 đạt giá trị nhỏ nhất.
3. Giải bất phương trình
2 4
0,5 2 16
log 4log 4 logx x x
…Hết…
(Cán bộ coi thi không giải thích gì thêm)
ĐÁP ÁN THANG ĐIỂM ĐỀ THI THỬ KHỐI A
Câu
ý
Nội dung
Điểm
2
1
1
TXĐ D =
Sự biến thiên : y’ = 3x2 + 6x + 3 = 3(x + 1)2
0x
Hàm số đồng biến trên
Hàm số không có cực trị
Giới hạn :
lim
xy
 
Bảng biến thiên
x

0

y’
+ 0 +
y


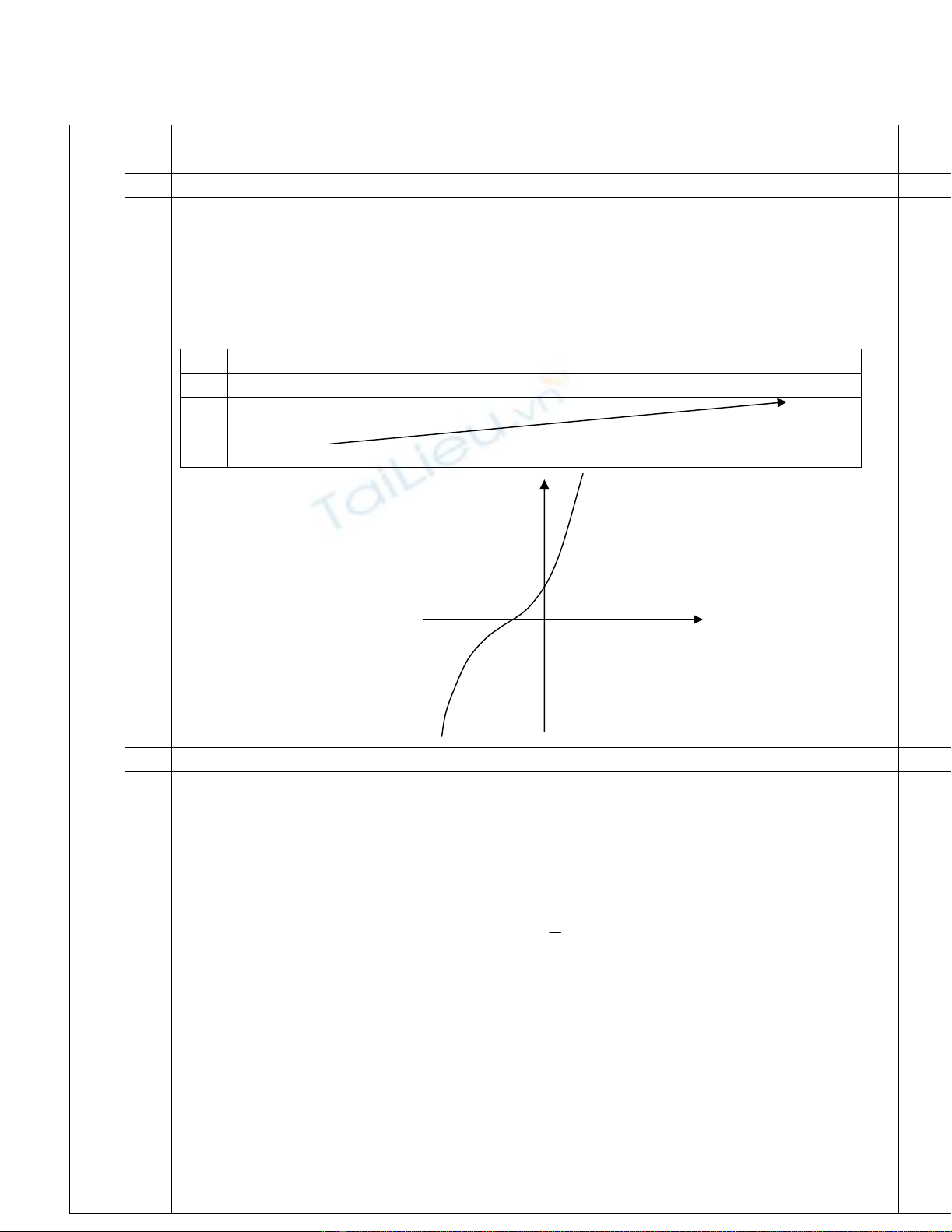
Đồ thị y
1
-1 O x
025
023
025
025
2
1
I
Phương trình hoành độ giao điểm của đồ thị (Cm) và đường thẳng y = x + 1
x3 + 3x2 + mx = 0
2
0
3 0
x
x x m
Đường thẳng y = x + 1 cắt đồ thị (Cm) tại 3 điểm phân biệt khi và chỉ khi
2
( ) 3 0g x x x m
có hai nghiệm phân biệt khác 0 khi và chỉ khi
9
0 9 4 0 4
(0) 0 0 0
mm
g m m
(*)
Khi đó hoành độ của B và C thỏa mãn
3
.
B C
B C
x x
x x m
(1)
Ta có f’(x) = 3x2 + 6x + m + 1
Hệ số góc các tiếp tuyến tại B và C là f’(xB) =
2
3 6 1
B B
x x m
,f’(xC) =
2
3 6 1
C C
x x m
Các tiếp tuyến tại B và C vuông góc khi và chỉ khi f’(xB). f’(xC) = -1
(
2
3 6 1
B B
x x m
).(
2
3 6 1
C C
x x m
) = - 1
(
2
3 6
B B
x x
)(
2
3 6
C C
x x
)+ (m + 1)(
2
3 6
B B
x x
+
2
3 6
C C
x x
) + (m + 1)2 = - 1
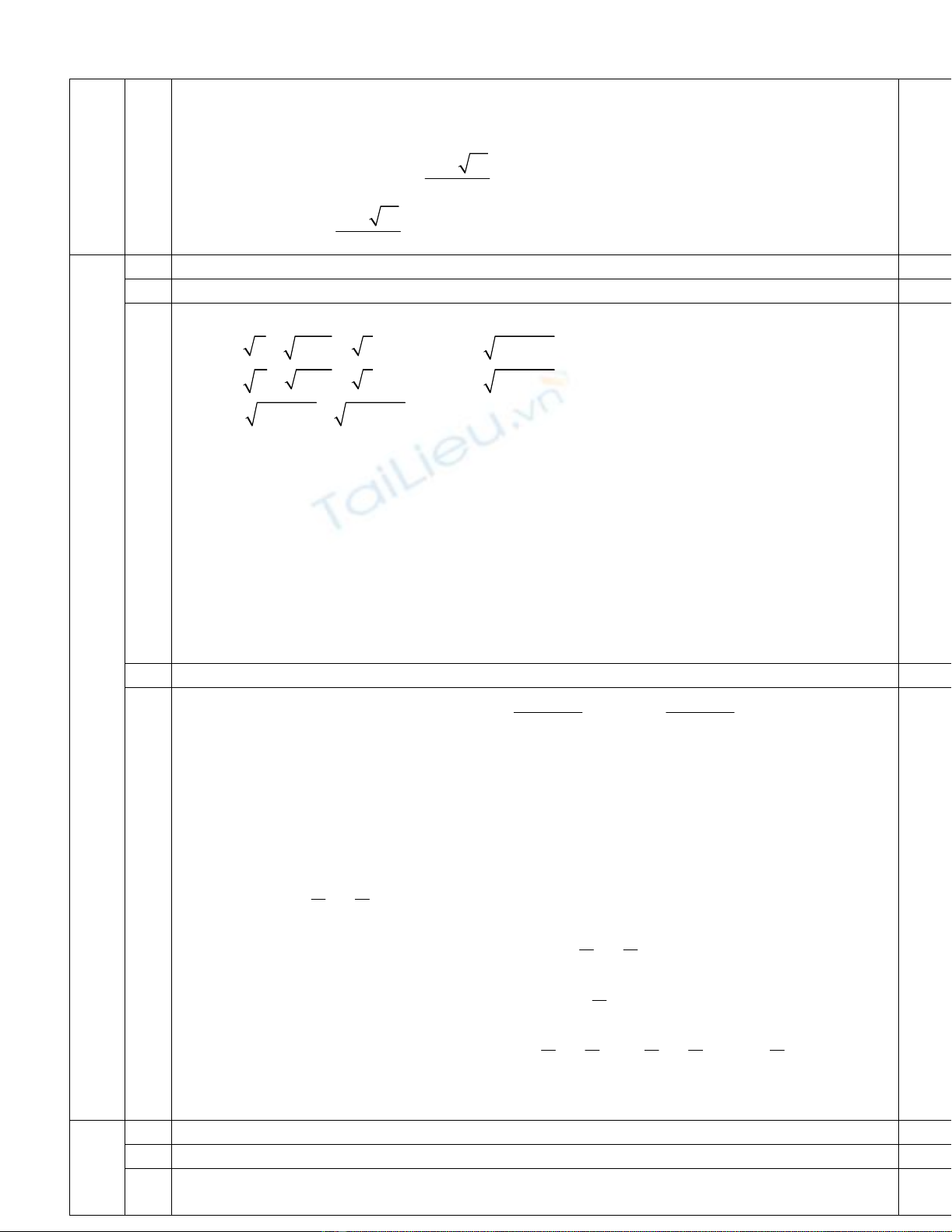
2 2
9( . ) 18 ( ) 36 3( 1)(( ) 2 3( ))
B C B C B C B C B C B C B C
x x x x x x x x m x x x x x x
025
025
025
…Hết…
(Cán bộ coi thi không giải thích gì thêm)
+m2 + 2m + 2 = 0
Kết hợp với (1) ta được
9m2– 54m + 36m + 3(9 – 2m - 9) + m2 + 2m + 2 = 0
5m2– 11m + 1 = 0
11 91
10
m
thỏa mãn điều kiện (*)
Kết luận: Với
11 91
10
m
thì thỏa mãn yêu cầu.
025
2
1
1
Điều kiện:
0 3,0 3x y
Ta có
3 3
3 3
x y
y x
2 (3 ) 0
2 (3 ) 0
x y x y
y x y x
(3 ) (3 ) 0
(3 ) 0
(3 ) 0
x y y x
x y
y x
0
0
3
3
x
y
x
y
Kiểm tra ta thấy
0 3
,
0 3
x x
y y
thỏa mãn.
Kết luận : Hệ có hệ có hai nghiệm
0 3
,
0 3
x x
y y
025
025
025
025
2
1
II
Ta có
23sin2sinsin 222 xxx
2
1 os2x 1 os6x
sin 2 2
2 2
c c
x
2
2
os2 os6 2(1 sin 2 ) 0
os2 . os4 os 2 0
os2 ( os4 os2 ) 0
c x c x x
c x c x c x
c x c x c x
os2 0c x
hoặc cos4x + cos2x = 0
os2 0 4 2
c x x k
,
cos4x + cos2x = 0
os4 os( 2 )c x c x
6 3
2
x k
x k
Kết luận: Phương trình có ba họ nghiệm
4 2
x k
,
à
6 3 2
x k v x k
025
025
025
025
2
1
1
III
Đường tròn tâm I(2; 1) bán kính R = 1 có phương trình : (x - 2)2 + (y - 1)2 = 1
…Hết…
(Cán bộ coi thi không giải thích gì thêm)
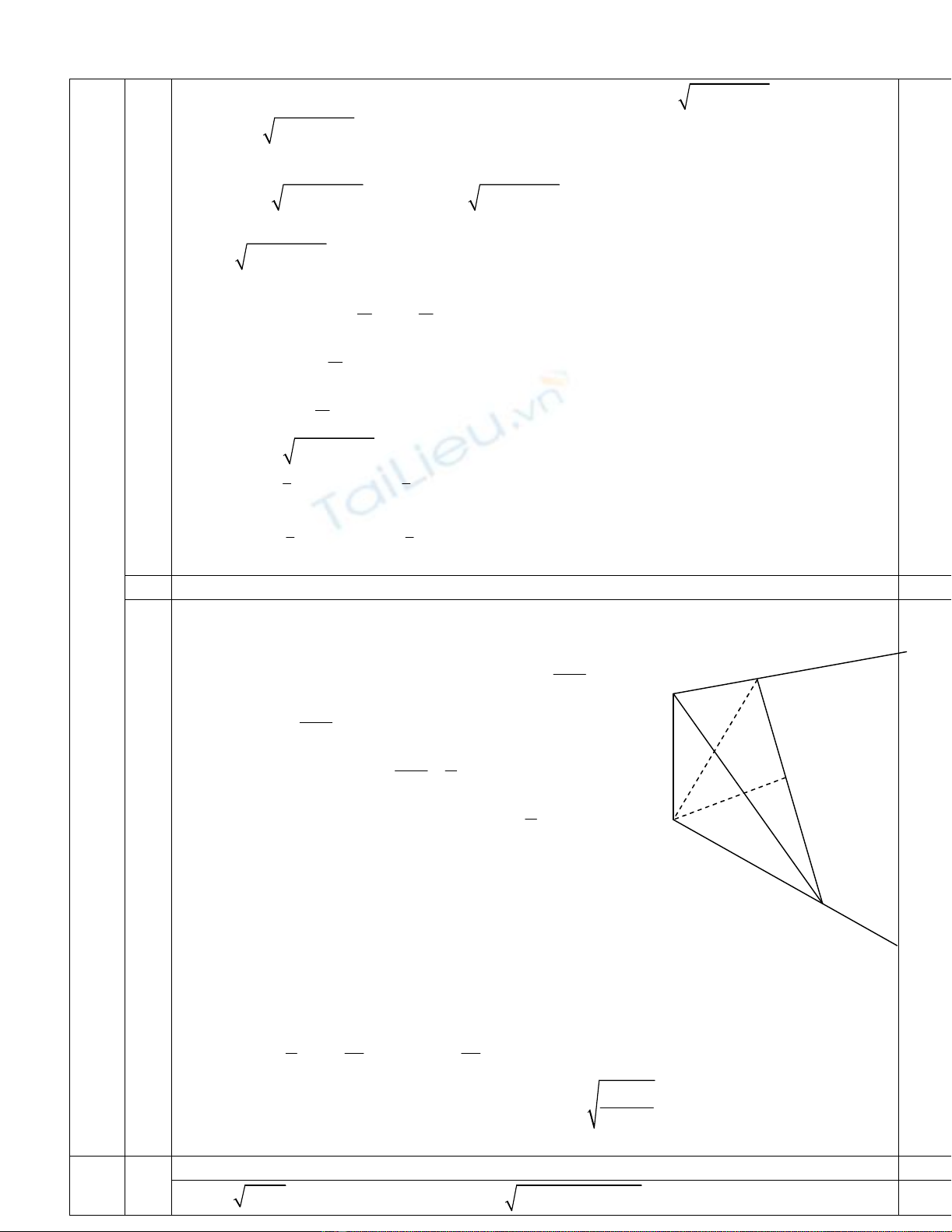
Điều kiện:
1 3x
. Từ phương trình đường tròn ta có
2
1 1 ( 2)y x
với
1y
Và
2
1 1 ( 2)y x
với
1y
.
Thể tích vật thể cần tìm
3 3
2 2
2 2
1 1
32
1
1 1 ( 2) 1 1 ( 2)
4 1 ( 2)
V x dx x dx
x dx
Đặt x – 2 = sint với
2 2
x
.
x = 1
t =
2
x = 3
t =
2
dx = costdt,
2
1 ( 2)x
= cost.
Vậy V =
22
2
4 osc tdt
=
22
2
2 (1 os2 ) 2c t dt
025
025
025
025
2
1
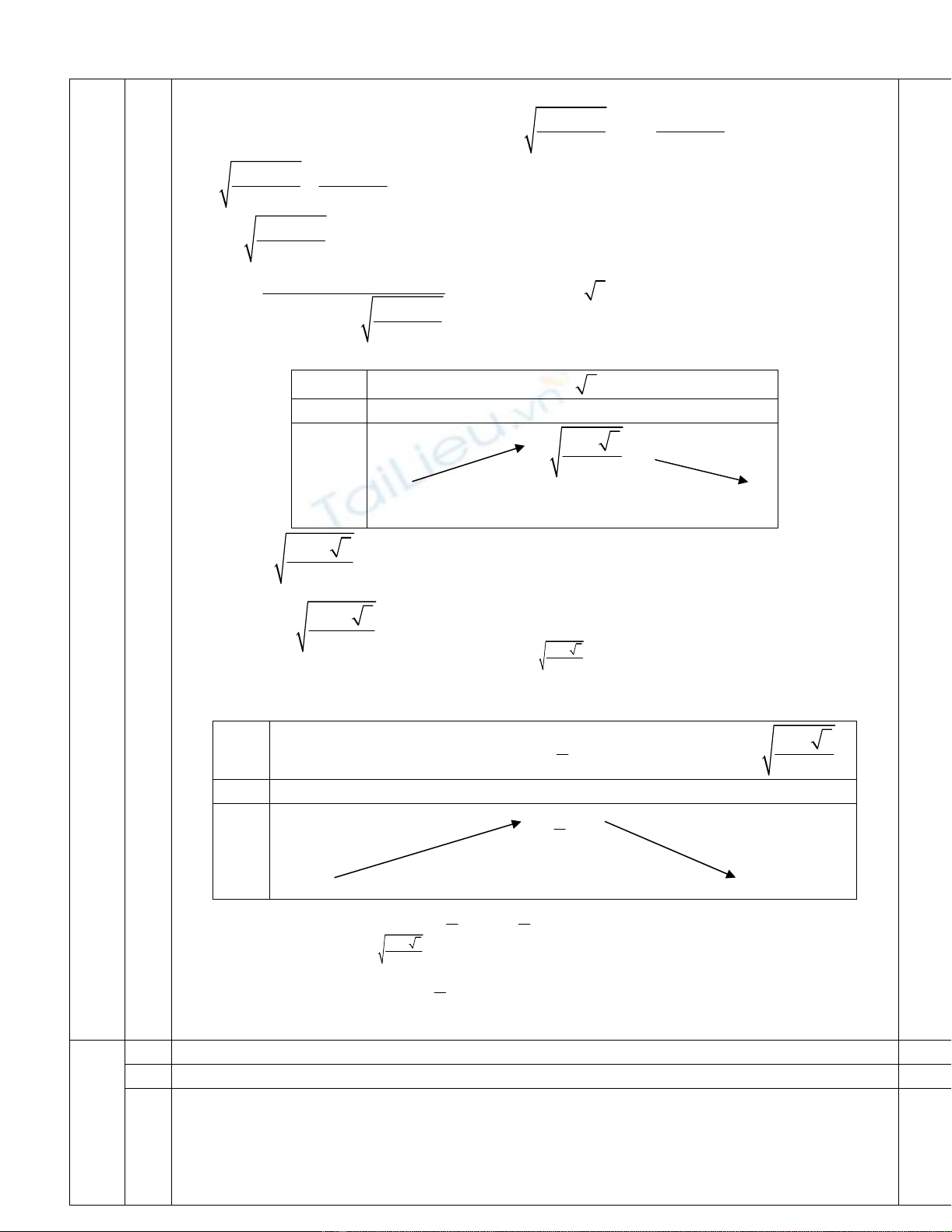
a) Gọi I là trung điểm của MN.
Ta có
,BN AB BN AM BN BM
x
do đó tam giác BMN vuông tại B suy ra BI =
2
MN
, A M
tương tự AI =
2
MN
.
Vậy AI = BI = MI = NI =
2
MN
=
2
b
I
Tâm mặt cầu ngoại tiếp là I, bán kính R =
2
b
B
b) Đặt AM = x > 0, BN = y > 0 N
Tam giác ABN vuông tại B nên AN2 = AB2 + BN2y
Tam giác AMN vuông tại A nên MN2 = AM2 + AN2
Suy ra b2 = MN2 = AM2 + AB2 + BN2 = x2 + a2 + y2
Do đó x2 + y2 = b2– a2 không đổi.
Tứ diện ABMN có đáy là ABM, đường cao BN.
Thể tích
2 2 2 2
1 1 1
ax ( ) ( )
6 12 12
V y a x y a b a
.
Thể tích tứ diện ABMN lớn nhất khi AM = BN =
2 2
2
b a
.
025
025
025
025
1
IV
Ta có
2 2
( 1)( 1) ( 1) ( 1)x x x m x x x
…Hết…
(Cán bộ coi thi không giải thích gì thêm)
Điều kiện
1x
Khi đó bất phương trình tương đương với
2 2
1 1
1 1
x x
m
x x x x
2 2
1 1
1 1
x x m
x x x x
(*)
Đặt t =
2
1
1
x
x x
, bất phương trình (*) có dạng : t – t2
m
(1)
Ta có
2
2 2 2
2 2
' , ' 0 1 3
1
2( 1) 1
x x
t t x
x
x x x x
.
Bảng biến thiên
x
-1
1 3

t’
+ 0 -
t
3 2 3
3
0 0
Vậy
11 7 3
0; 13
t
. Bất phương trình đã cho có nghiệm khi và chỉ khi (1) có
nghiệm
11 7 3
0; 13
t
khi và chỉkhi
11 7 3
[0; ]
13
ax ( )
t
M f t m
với f(t) = t – t2
f’(t) = 1 – 2t
Bảng biến thiên
t
0
1
2
3 2 3
3
f’(t)
+ 0 -
f(t)
1
4
Từ bảng biến thiên :
11 7 3
[0; ]
13
1 1
ax ( ) 4 2
t
M f t khi x
Vậy ycbt tương đương với
1
4
m
025
025
025
025
3
1
1
Va
Đường thẳng đi qua P(3 ; 1) có dạng
:ax 3 0by a b
Đường thẳng
tạo với hai đường thẳng
1 2
àd v d
một tam giác cân có đỉnh là giao của
1 2
àd v d
khi và chỉ khi
1 2
( , ) ( , )d d
1 2
os( ,d ) os( ,d )c c
025