>> http://tuyensinh247.com/ - Học là thích ngay! 1
TRƯỜNG THPT NGUYỄN TRUNG THIÊN
ĐỀ THI THỬ KÌ THI QUỐC GIA NĂM 2015
TỔ TOÁN
Môn TOÁN (lần 1)
Thời gian làm bài: 180 phút
Câu 1 ( ID: 83043 ) (2,0 điểm). Cho hàm số
a)Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1).
b) Chứng minh rằng đường thẳng luôn cắt (C) tại 2 điểm phân biệt A, B.
Tìm m để tọa độ đoạn AB = √ .
Câu 2 ( ID: 83044 ) (1,0 điểm). Giải phương trình: c
Câu 3 ( ID: 83045 ) (1,0 điểm). Tính tích phân ∫
Câu 4 ( ID: 83046 ) (1,0 điểm). Giải phương trình: √
Câu 5 ( ID: 83047 ) (1,0 điểm). Một tổ học sinh gồm có 5 học sinh nam và 7 học sinh nữ.
Chọn ngẫu nhiên 2 học sinh đi chăm sóc bồn hoa. Tính xác suất để học sinh được chọn đi
chăm sóc bồn hoa có cả nam và nữ.
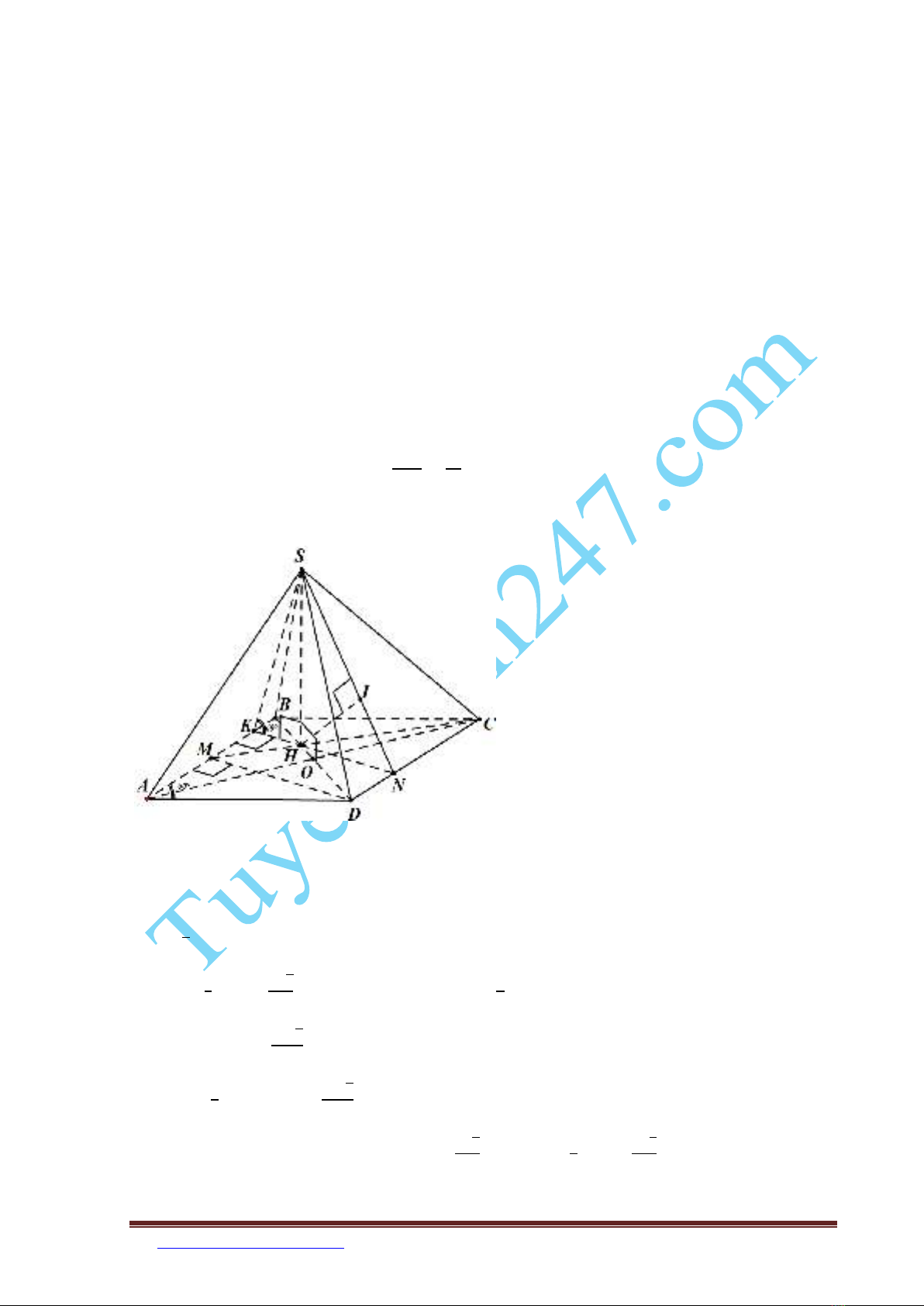
Câu 6 ( ID: 83048 ) (1,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a,
góc
. Hình chiếu vuông góc của đỉnh S lên mặt phẳng (ABCD) là trọng tâm
. Góc giữa mặt phẳng (ABCD) và mặt phẳng (SAB) bằng . Tính thể tịch khối chóp
S.ABCD và khoảng cách từ B đến mặt phẳng (SCD).
Câu 7 ( ID: 83049 ) (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có
trung điểm cạnh BC là Điểm nằm trên đường thẳng Δ chứa đường cao
qua đỉnh B. Đường thẳng AC qua . Tìm tọa độ các đỉnh của có đường kính AD
với .
Câu 8 ( ID: 83050 ) (1,0 điểm): Giải phương trình: (√ )
(√ )
Câu 9 ( ID: 83051 ) (1,0 điểm). Cho là ba số thực dương thỏa mãn .
Tìm giá trị nhỏ nhất của biểu thức sau:
>> http://tuyensinh247.com/ - Học là thích ngay! 2
ĐÁP ÁN
Câu 1 (2,0 đ)
a). (1 điểm)
+ Tập xác định:
.
+ Sự biến thiên:
-Chiều biến thiên:
. (0,25đ)
Hàm số nghịch biến trên từng khoảng
và
-Giới hạn, tiệm cận:
=> tiệm cận ngang của đồ thị là y =
(0,25đ)
=> Tiệm cận đứng của đồ thị là x =
-Bảng biến thiên: (0,25đ)
-Đồ thị: (0,25đ)
b) (1 điểm)
Số giao điểm của đường thẳng và đồ thị bằng số nghiệm của PT:
x
y’
y
>> http://tuyensinh247.com/ - Học là thích ngay! 3
(1)⇔{
⇔ 5đ
Phươ trì h có b ệt thức có
nghiệ phâ b ệt ê uô cắt (C) tạ đ ể phâ b ệt A, B 5đ
Gọi thì à h ệm của PT và
=> √ √ √ . Mặt khác:
(0,25đ)
Từ đó ta có: √ ⇔ ⇔ ⇔ .
Vậy (0,25đ)
Câu 2 (1,0 đ)
c ⇔ c c (0,25đ)
⇔ c c ⇔ c 5đ
⇔c
⇔
. 5đ
Phươ trì h có các h ệ à :
, 5đ
Câu đ
Đặt {
{
5đ
]
∫*
+
(0,25đ)
=
(0,25đ)
= (
)
(0,25đ)
Câu 4 (1,0 đ)
√
Điều kiện √ (0,25đ)
>> http://tuyensinh247.com/ - Học là thích ngay! 4
(*)⇔
⇔ ] 5đ
⇔ ⇔*
5đ
Đối chiếu đ ều kiệ thì phươ trì h có h ệm 5đ
Câu 5 đ
Gọi à khô a ẫu: A à b ến cố “ học h được chọn gồm cả a và ữ” 5đ
Số phần tử khô a ẫu:
5đ
Số trường hợp thuận lợ ch A à
5 5đ
Xác uất của biến cố A à
5 5đ
Câu đ
Gọi H là trọng tâm ΔABC, K là hình chiếu của H lên AB suy ra:
. DM là đường cao tam giác ABD => HK // DM
=>
√
ta
(0,25đ)
√
.
√
(0,25đ)
Kéo dài KH cắt DC tại N => √
√
(0,25Đ)
>> http://tuyensinh247.com/ - Học là thích ngay! 5
Gọi IH là đường cao của ΔSHN => ( ) . Ta có
√
√
Vậy ( )
√
(0,25đ)
Câu 7 (1,0 đ)
Gọi H là trực tâm ΔABC => BDCH là hình bình hành
=> M là trung điểm của DH => H (2; 0) (0,25đ)
Đường thẳng AC đi qua F (1; 3) và nhận
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
làm véc tơ pháp tuyến nên phương
trình của AC là: . Đường cao BH qua H và E nên phương trình của BH là:
(0,25đ)
Gọi tọa độ của B, C là:
Do M là trung điểm BC nên ta có hệ:
,
⇔,
5 Vậy B (1; -1) C(5;-1) (0,25đ)
Đường cao AH đi qua H và vuông góc với BC nên AH có phương trình: x = 2. Tọa độ A thỏa
mãn hệ:
{
{
Vậy A(2;2)
Câu 8 (1,0 đ)
Phương trình biến đổi thành: (√ ) √ (0,25đ)
Đặt . Xét hàm số √ , phương trình trở thành