Phan Hòa Đại Đề thi toán vào 10 Lê Quý Đôn -Bình Định
SỞ GIÁO DỤC – ĐÀO TẠO KỲ THI TUYỂN SINH VÀO LỚP 10 THPT NĂM HỌC 2013-2014
BÌNH ĐỊNH TRƯỜNG THPT CHUYÊN LÊ QUÝ ĐÔN
Đề chính thức Môn thi: Toán ( Chuyên toán - tin )
Ngày thi: 15/6/2013 Thời gian làm bài: 150’
Bài 1: ( 2,5 đ) Cho biểu thức:
x 2 x 2
Q x x
x1
x 2 x 1






( Với x ≥ 0 ; x ≠ 1)
1. Rút gọn Q
2.Tìm các giá trị nguyên của x để Q nhận giá trị nguyên
Bài 2: (2 đ) Giải hệ phương trình:
x 2 3 13
x 3 y 1 10
3 2y 4 11
x 3 y 1 6



Bài 3: (1,5 đ) Cho a,b,c là các số thực dương. CMR :
bc ca ab a b c
a b c
.
Bài 4: (3 đ) Cho đường tròn (O,R) và đường thẳng (d) không đi qua O cắt đường tròn tại hai
điểm A,B. Lấy một điểm M trên tia đối của tia BA kẻ hai tiếp tuyến MC, MD với đường tròn (
C,D là các tiếp điểm). Gọi H là trung điểm của AB.
1. CMR các điểm M,D,O,H cùng nằm trên một đường tròn.
2. Đoạn OM cắt đường tròn tại điểm I. CMR I là tâm đường tròn nội tiếp ∆MCD.
3. Đường thẳng qua O, vuông góc với OM cắt các tia MC, MD theo thứ tự tại P và Q. Tìm
vị trí điểm M trên (d) sao cho diện tích ∆ MPQ bé nhất.
Bài 5: (1 đ) : Không dùng máy tính, hãy rút gọn biểu thức:
A 7 13 7 13 2
---*---
Phan Hòa Đại Đề thi toán vào 10 Lê Quý Đôn -Bình Định
HƯỚNG DẪN GIẢI
Bài 1: ( 2,5 đ) Cho biểu thức:
x 2 x 2
Q x x
x1
x 2 x 1






( Với x ≥ 0 ; x ≠ 1)
1.Rút gọn Q
2
2
x 2 x 2 x 2 x 2
Q x x x x 1
x1
x 2 x 1 x 1 x 1
x1
x 2 x 1 x 2 x 1 x x 2 x x 2 2x
. x x 1 . x x1
x 1 x 1
x 1 x 1






 





2.Tìm các giá trị nguyên của x để Q nhận giá trị nguyên:
Q=
2x 2
2 Q x 1 U(2)= 2; 1;1;2 x 1;0;2;3
x 1 x 1

Kết hợp với điều
kiện =>
x 0;2;3
Vậy với
x 0;2;3
thì Q nhận giá trị nguyên.
Bài 2: (2 đ) Giải hệ phương trình:
x 2 3 13 1 3 13 1 3 3
1
x 3 y 1 10 x 3 y 1 10 x 3 y 1 10
3 2y 4 11 3 2 11 3 2 1
2
x 3 y 1 6 x 3 y 1 6 x 3 y 1 6

( ĐK x ≠ 3; y ≠ -1)
Đặt a =
; b=
1
y1
ta được hệ :
11
31
a 3b a x 13
x 3 10
10 10
... (TMDK)
11
1 1 y 14
3a 2b b y 1 15
6 15




Vậy hệ pt có nghiệm duy nhất (x;y) = (13;14)
Bài 3: (1,5 đ) Cho a,b,c là các số thực dương. CMR :
bc ca ab a b c
a b c
.
a,b,c là các số thực dương => Theo BĐT Cô-Si ta được:
bc ca bc ca
2 . 2c
a b a b
ca ab ab ca bc ca ab bc ca ab
2 . 2a 2 2. a b c a b c
b c c b a b c a b c
bc ab bc ab
2 . 2b
a c a c




Bài 4: (3 đ)
1. CMR các điểm M,D,O,H cùng nằm trên một đường tròn.
HA=HB => OH AB ( đường kính đi qua trung điểm một dây không đi qua tâm) =>
OHM
= 900
Lại có
ODM
= 900 ( Tính chất tiếp tuyến)
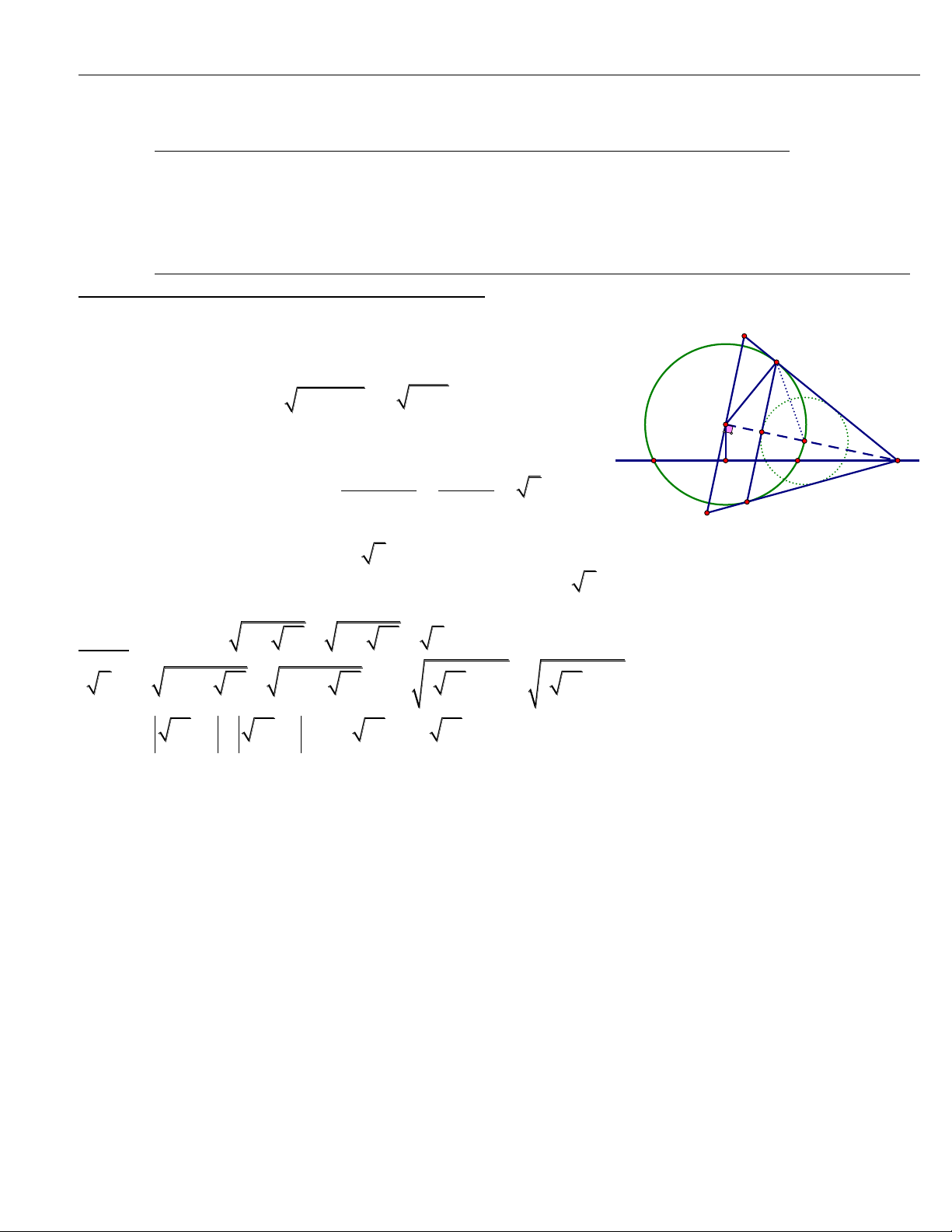
Phan Hòa Đại Đề thi toán vào 10 Lê Quý Đôn -Bình Định
(
d
)
P
Q
I
H
C
D
B
A
O
M
Suy ra
OHM
=
ODM
= 900 => H,D cùng nhìn đoạn OM dưới 1 góc vuông => H,D cùng nằm trên
đường tròn đường kính OM => các điểm M,D,O,H cùng nằm trên đường tròn đường kính OM
2. Đoạn OM cắt đường tròn tại điểm I. CMR I là tâm đường tròn nội tiếp ∆MCD.
Ta có:
COI DOI
( Tính chất hai tiếp tuyến cắt nhau)=>
CI DI
=>
CDI DIM
=> DI là phân
giác trong của ∆ MCD (1)
Lại có MI là đường phân giác trong của ∆ MCD ( Tính chất hai tiếp tuyến cắt nhau) (2)
Từ (1) và (2) suy ra I là tâm đường tròn nội tiếp ∆ MCD
3. Đường thẳng qua O, vuông góc với OM cắt các tia MC, MD theo thứ tự tại P và Q. Tìm vị trí
điểm M trên (d) sao cho diện tích ∆ MPQ bé nhất.
Ta có ∆MOD = ∆MOP (g-c-g) => S∆ MPQ= 2 S∆ MOQ =OD.MQ = R.MQ
=> S∆ MPQ nhỏ nhất MQ nhỏ nhất (3)
Theo BĐT Cô – si cho hai số không âm ,
ta có: MQ = MD+DQ ≥
2
2 MD.DQ 2 OD 2OD 2R
( Vì ∆ MOD vuông tại O có đường cao OD nên OD2=MD.DQ )
Dấu “=” xảy ra
MD= DQ
∆OMQ vuông cân tại O
0
OMD 45
OM
0
OD R 2.R
sin OMD sin 45
(Vì ∆ ODM vuông nên OD= OM.sinOMD )
Vậy MQmin = 2R
OM =
2
R (2)
Từ (3) và (4) suy ra khi M nằm trên (d) cách O một khoảng
2
R thì S∆ MPQ nhỏ nhất là R.2R=2R2 (
d.v.d.t)
Bài 5: (1 đ) :
A 7 13 7 13 2
.Ta có:
22
2.A 14 2 13 14 2 13 2 13 1 13 1 2
13 1 13 1 2 13 1 13 1 2 0
A0
