228
Chương 9
ĐỒ HỌA TRONG MATLAB
9.1 ĐỒ HỌA HAI CHIỀU
Rất nhiều các bài toán khoa học, kĩ thuật và kinh tế cần được diễn giải và
phân tích để rút ra các thông tin liên quan. Đặc biệt trong hầu hết lĩnh vực mô
phỏng các quá trình khoa học và công nghệ chúng ta phải đối mặt với những tập
dữ liệu rất lớn mà không thể phân tích mà thiếu các phần mềm biểu diễn dữ liệu.
Trong phần này chúng ta sẽ nghiên cứu các công cụ biểu diễn dữ liệu hai
chiều và quá trình biến đổi dữ liệu theo thời gian. Trong các chương trước, chúng
ta đã được làm quen với một số lệnh vẽ đồ thị 2 chiều như: plot, xlabel, ylabel,
text, gtext, loglog, semilogx, semilogy, axis, grid on, hold on, figure và legend.
9.1.1 Hệ toạ độ Semilogarithm
Các thủ tục loglog,semilogx, semilogy thích hợp các tập dữ liệu biến đổi
lớn, đặc biệt các quá trình biến đổi (tiệm cận) theo hàm mũ, hàm luỹ thừa.
Thí dụ 1. Vẽ đồ thị của hàm ( )
1
x
x
f x
e
bằng plot và semilogy:
Hình 9.1 Vẽ đồ thị hàm ( )
1
x
x
f x
e
bằng hàm PLOT
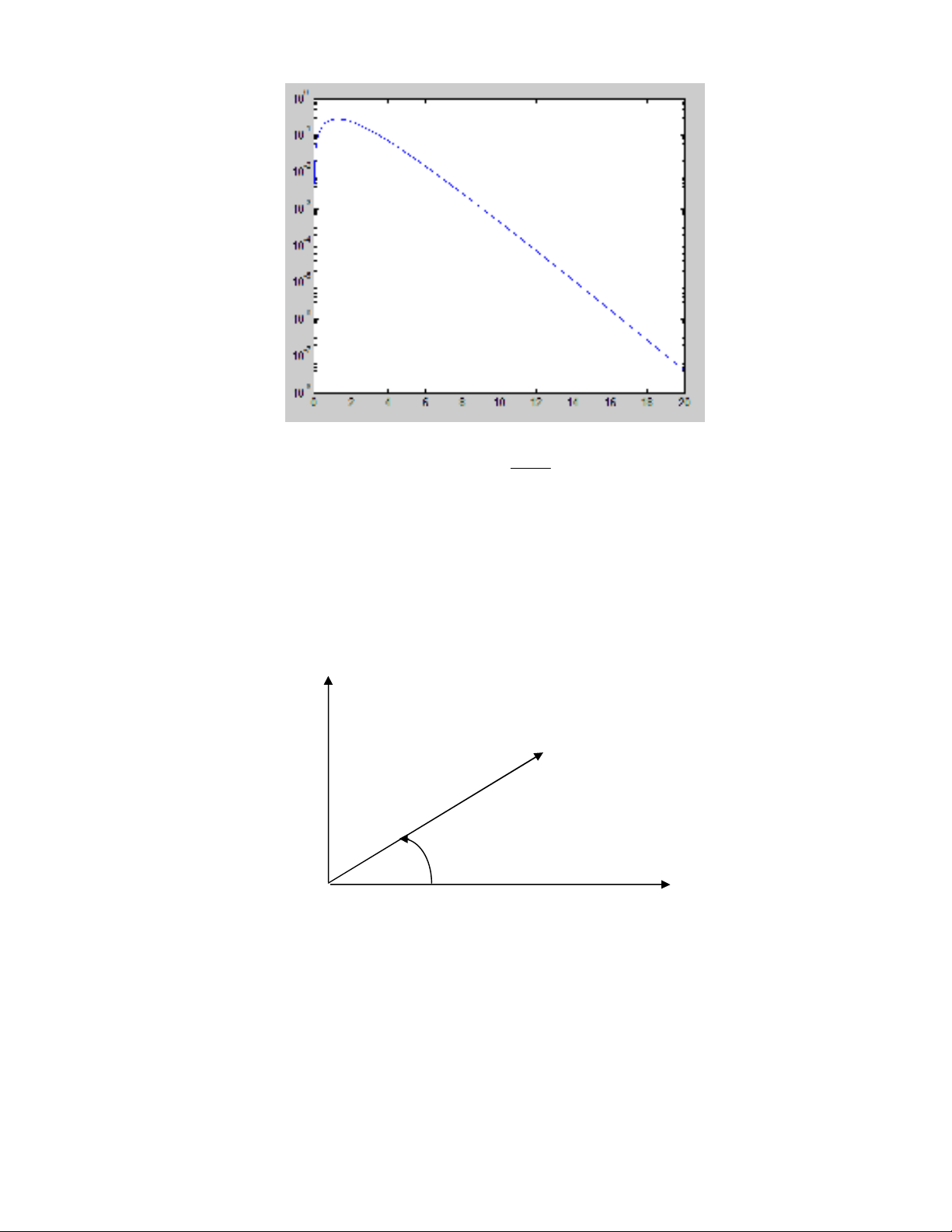
229
Hình 9.2 Vẽ đồ thị hàm ( )
1
x
x
f x
e
bằng hàm SEMILOGY
9.1.2 Hệ toạ độ cực
Trong một số ứng dụng, việc mô tả bài toán trong hệ toạ độ nào đó có lợi
hơn là mô tả dữ liệu trong toạ độ Đề-các chuẩn. Nó tạo cho ta cảm giác như
đang quan sát dữ liệu từ một hệ toạ độ xác định. Một trong các hệ toạ độ như vậy
là hệ toạ độ cực, trong đó dữ liệu được được cho bởi khoảng cách từ cực và các
góc giữa vector bán kính với một trục cố định. Thí dụ như nghiên cứu tốc độ của
thuyền buồm chịu ảnh hưởng của tốc độ và hướng gió.
y
M (x,y)
(r, )
r
O x
Hình 9.3 Hệ tọa độ Đề các và hệ tọa độ cực
Hàm POLAR
Cú pháp:
polar (Theta, R,Symbol)
230
Giải thích. Hàm POLAR vẽ đồ thị hàm số trong hệ tọa độ cực.
- Theta : vector trị số góc từ trục cố định đến bán kính, đơn vị đo là radian;
- R : giá trị của hàm R=R(Theta) ;
- Symbol là một xâu qui định kiểu vẽ (xem plot).
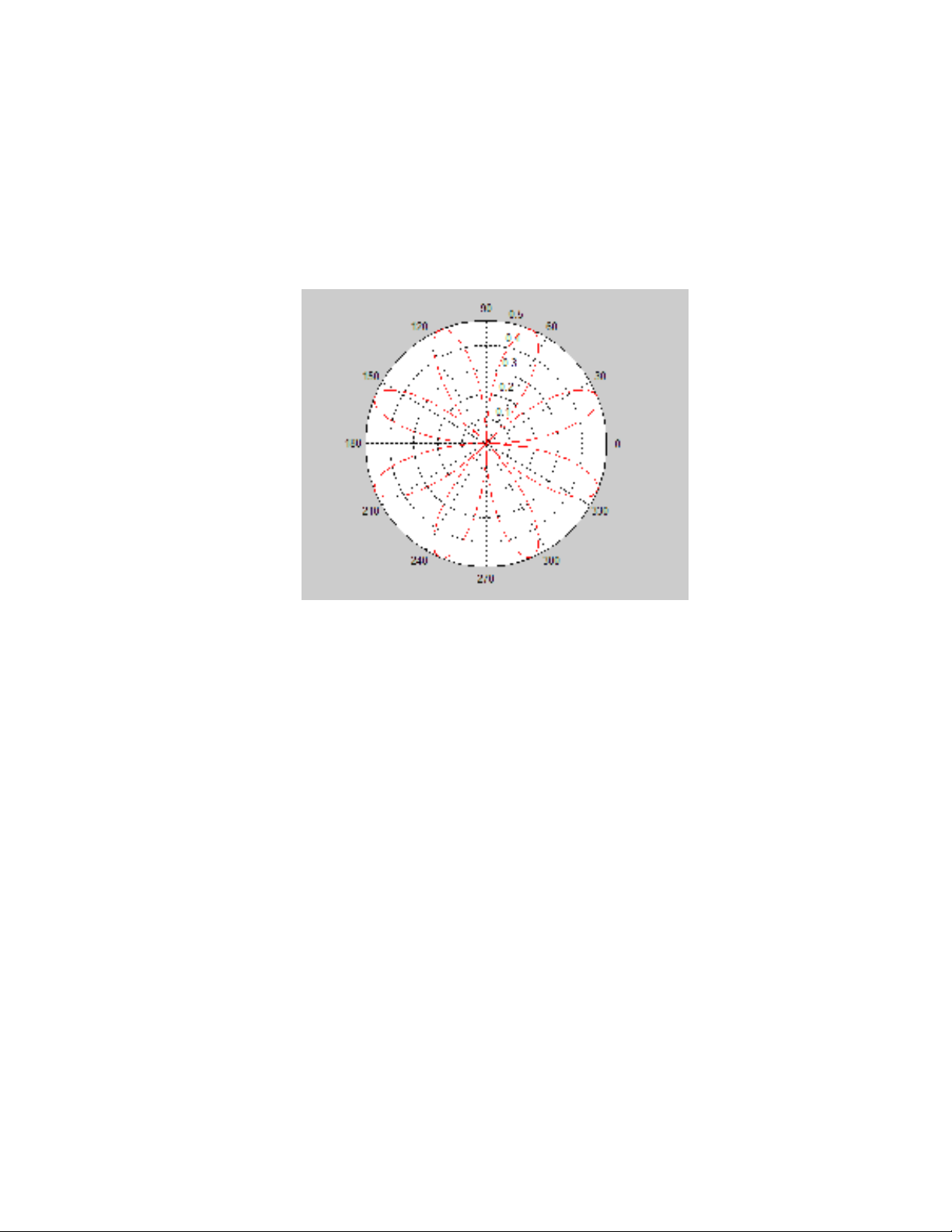
Thí dụ 2.
>> t = 0:.01:2*pi;
>> polar(t,sin(2*t).*cos(2*t),'--r')
Hình 9.4 Vẽ đồ thị hàm số bằng hàm POLAR
9.1.3 Lưu trữ đồ thị
Có thể lưu trữ đồ thị vào file hoặc in đồ thị bằng hàm PRINT.
Cú pháp:
print [-driver] [-options] [ filename]
Giải thích.
print : in đồ thị hiện tại ra máy in mặc định;
print –f2 hay print(2) : in đồ thị figure (2);
print <filename> : lưu đồ thị dưới dạng file PostScript, mặc định *.ps.
Tham số driver: thường bắt đầu bằng chữ ‘-d’.
-dwin : đưa figure hiện tại ra máy in đen trắng;
-dwinc : đưa figure hiện tại ra máy in màu;
-dbitmap : đưa figure vào clipboard dưới dạng Bitmap file;
231
-djpeg<nn> : đưa figure vào clipboard dưới dạng JPEG image với chất
lượng nn (mặc định nn=75).
-dps : đưa figure vào file PostScript (*.ps) dùng cho máy in đen trắng;
-dpsc : đưa figure vào file PostScript (*.ps) dùng cho máy in màu;
-deps : đưa figure vào file Encapsulated PostScript (*.eps) dùng máy in đen
trắng;
-depsc : Đưa figure vào file Encapsulated PostScript (*.eps), máy in màu.
Tham số options: chỉ sử dụng cho PostScript driver.
-append : thực hiện append, không overwrite đối với PostScript file;
-r<n> : xác định độ phân giải dpi cho hình vẽ. Mặc định là -r150.
Thí dụ 3.
>> print -depsc -r300 Matine %% Lưu Figure hiện tại với độ phân giải
%% 300 dpi vào file Matine.eps.
Có thể sử dụng lệnh print như gọi một hàm:
print(‘-device’,’-options’,’ filename’)
Thí dụ 4.
>> print(‘-depsc’,’-r300’,’Matin’)
9.1.4 Biểu đồ (Bar chats)
Khi xử lí các dữ liệu thống kê, có thể biểu diễn chúng dưới dạng một biểu
đồ bằng hàm BAR như là một đồ thị 2 chiều.
Các phương án sử dụng hàm BAR:
bar(X,Y) : vẽ biểu đồ các cột của một ma trận Y cỡ M×N như M nhóm dữ
liệu của N bộ số liệu. Vector X phải đơn điệu tăng hoặc giảm.
bar(Y) : mặc định của X là 1:M.
bar(X,Y,width) hoặc bar(Y,width) : width xác định độ rộng của các cột trên
biểu đồ. Mặc định của width là 0.8. Nếu width > 1 thì các cột biểu đồ sẽ chồng
ken vào nhau.
bar(X,Y,'grouped') : vẽ biểu đồ theo nhóm cột đứng (mặc định).
bar(X,Y,'stacked') : vẽ biểu đồ theo nhóm xếp đống .
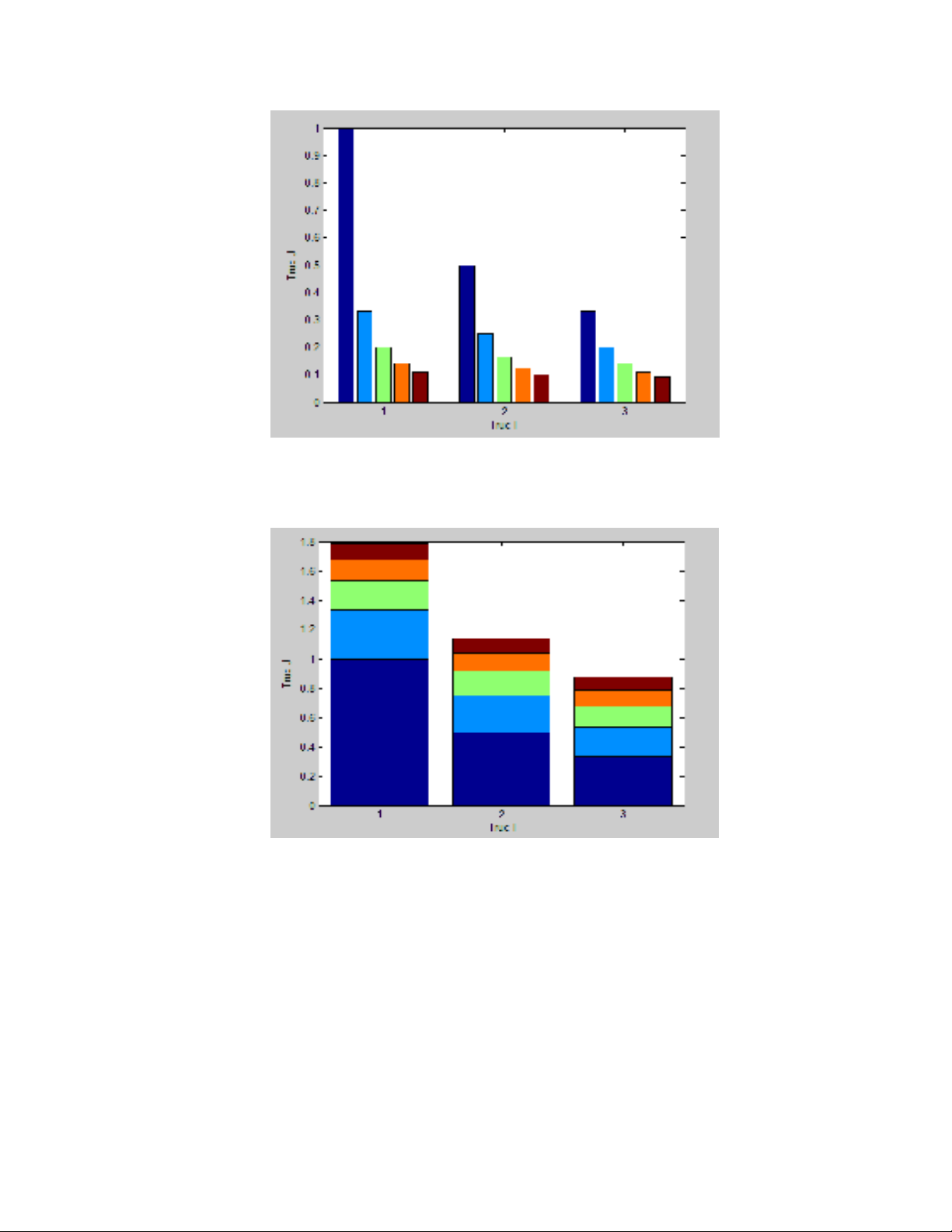
Thí dụ 5.
>> Y=hilb(10); y=Y([1:3],[1:2:9]);
>> figure(1), bar(y);
>> xlabel(‘ Truc I’);ylabel(‘Truc J’);
>> figure(2), bar(y,’stacked’);
>> xlabel(‘ Truc I’);ylabel(‘Truc J’);
232
Figure 1
Hình 9.5 Đồ thị bar ‘group’
Figure 2
Hình 9.6 Đồ thị bar ‘stacked’
9.1.5 Biểu diễn sai số ( Error Bars)
Khi xử lí dữ liệu, ta thường quan tâm đến mức độ thiếu chính xác của chúng
do dung sai thiết bị hay sự không hoàn hảo của môi trường thực nghiệm. Để mô
tả sai số có thể sử dụng hàm ERRORBAR .