0
K
KỸ
ỸTHU
THUẬ
ẬT L
T LẬ
ẬP TRÌNH
P TRÌNH
KỸTHUẬT PHÁT TRIỂN CHƯƠNG TRÌNH
NỘI DUNG
Hàm và Thủtục
Phát triển chương trình bằng phương pháp tinh
chỉnh dần từng bước.
Định nghĩa và sửdụng hàm trong ngôn ngữC
Hàm/thủtục đệ quy
1
H
HÀ
ÀM V
M VÀ
ÀTH
THỦ
ỦT
TỤ
ỤC
C
Thủtục (Procedures) và Hàm (functions) thểhiện
hai dạng của chương tình con (subprograms)
Cho phép lặp đi lặp lại một đoạn code hoặc một tính
toán nhất định.
Hàm/thủtục có thể được gọi từnhiều chỗkhác nhau
trong chương trình.
–Bằng cách thay thếmột dãy các chỉthịbởi một lệnh duy nhất
(lệnh gọi hàm/thủtục) sẽgiúp mã nguồn dễ đọc và dễduyệt lỗi
hơn.
Hàm có kết quảtrảvềcòn thủtục thì không.
2
Đối sốvà Tham biến (Arguments and Parameters)
Ví dụ
{ Cộng num1 và num2 rồi ghi kết quảvào biến sum}
Procedure Adder(num1 : real; num2 : real; var sum : real);
begin
sum := num1 + num2;
end;
Phạm vi của các biến:
•biến cục bộ trong chương trình con
•biến toàn cục
3
Vài điểm quan trọng về đối và tham biến của chương trình con:
Số lượng đối sốhay tham sốthực sự(arguments) nhất thiết phải
bằng sốtham biến (parameters)
Thứtựlà quan trọng. Đối số đầu tiên tương ứng với tham biến đầu
tiên, đối sốthứ k tương ứng với tham biến thứk, …
Kiểu dữliệu của mỗi đối sốphải tương thích với kiểu dữliệu của
tham biến tương ứng.
Tên không quan trọng. Tên của đối sốkhông nhất thiết phải giống
với tên tham biến tương ứng của nó.
Phân biệt hai cách truyền dữliệu cho hàm/thủtục: truyền theo
tham chiếu ( by reference ) hay truyền theo trị(by value)
4
Truyền theo tham chiếu: vịtrí trong bộnhớ (địa chỉ)
của đối số được truyền cho chương trình con, cho phép
chương trình con truy nhập tới biến thực sựvà thay đổi
nội dung của nó.
Truyền theo trị: giá trịcủa đối số được truyền cho
chương trình con, cho phép chương trình con truy nhập
đến “bản sao” của biến. Truyền theo trịbảo toàn nội
dung của biến ban đầu.
5
Ưu điểm của các hàm/thủtục
•Chia tách và kiểm soát (“Chia để trị”)
–Khả năng quản lý chương trình và phát triển
•Khả năng sửdụng lại các hàm/thủtục
–Sửdụng các hàm/thủtục đã có sẵn, chạy ổn định để xây
dựng các khối chương trình mới
–Tính trừu tượng: che dấu các chi tiết bên trong hàm
–Tránh phải lặp lại một đoạn chương trình (code)
6
C
Cá
ác bư
c bướ
ớc th
c thự
ực hi
c hiệ
ện ph
n phá
át tri
t triể
ển chương tr
n chương trì
ình
nh
Hiểu rõ yêu cầu bài toán: có thểdiễn đạt lại bài toán
bằng ngôn ngữ đặc tả, các kí hiệu toán học hay các
công thức.
•Mục tiêu chung của chương trình là gì?
•Chương trình cần dữliệu vào là gì?
•Dữliệu ra của chương trình là gì? sẽ như thếnào? kết xuất ra
đâu? (màn hình, máy in, đĩa?)
•Công thức tính hay cách xửlý thếnào để có kết quả(dữliệu)
ra?
•Dữliệu vào và ra nên ở định dạng nào?
7
C
Cá
ác bư
c bướ
ớc th
c thự
ực hi
c hiệ
ện ph
n phá
át tri
t triể
ển chương tr
n chương trì
ình
nh
Hình thành ý tưởng vềcách giải bài toán
•Chương trình có thể được phân tách thành các quá trình rời
rạc (các mô đun) như thếnào?
•Chương trình chính sẽsửdụng các mô đun này như thếnào?
Các mô đun giao tiếp với nhau như thếnào?
•Những mô đun này có cần tách thành các phần chức năng nhỏ
hơn?
8
Thiết kếthuật toán bằng phương pháp tinh chỉnh dần
từng bước.
Cài đặt chương trình theo thuật toán
•Viết chương trình chính (việc viết các mô đun như thếnào sẽ
hoàn thiện sau. Thay vào đó, có thểtạm đưa ra những lệnh
giả định để chương trình có thểhọat động. Điều này cho
phép thửnghiệm tính logic của chương trình chính).
•Cuối cùng, viết các mô đun. Kiểm nghiệm và duyệt lỗi từng mô
đun thật kỹrồi trước khi đưa vào chương trình chính. Nếu mô
đun được phân tách thành nhiều tiến trình nhỏ hơn thì phải
viết mã (code) cho các tiến trình này trước, thửnghiệm và
duyệt lỗi cẩn thận rồi mới ghép lại thành mô đun.
9
PHƯƠNG PH
PHƯƠNG PHÁ
ÁP TINH CH
P TINH CHỈ
ỈNH T
NH TỪ
ỪNG BƯ
NG BƯỚ
ỚC
C
Chiến lược thiết kếtừtrên xuống (top - down)
•Thiết kếgiải thuật từtổng thể đến chi tiết
•Module hoá bài toán
–Chia bài toán (module chính) thành các module con cho đến khi
mỗi module con là một bài toán đã biết cách giải quyết
•“Chia để trị”
–Chia (Divide): Chia bài toán lớn, thành nhiều bài toán nhỏ
–Trị(Conquer): Sửdụng thuật toán đệ quy để giải từng bài toán
nhỏ
–Kết hợp (Combine): Tạo ra lời giải cho bài toán cuối cùng bằng
cách sửdụng thông tin từkết quảgiải các bài toán nhỏ.
10
PHƯƠNG PH
PHƯƠNG PHÁ
ÁP TINH CH
P TINH CHỈ
ỈNH T
NH TỪ
ỪNG BƯ
NG BƯỚ
ỚC
C
Stepwise refinement
Tinh thần: module hoá bài toán, thiết kếkiểu top-down
•Bước 0. Trình bày ý chính của giải thuật bằng ngôn ngữtự
nhiên.
?Làm cái gì?
•Bước 1 trở đi: Chi tiết hoá dần những ý trong giải thuật, sử
dụng nhiều ngôn ngữgiảcode (giảmã − pseudo code) hơn.
Kết quảcuối cùng của quá trình tinh chỉnh là chương trình viết
trên ngôn ngữlập trình đã chọn trước với cấu trúc dữliệu dạng
lưu trữ, cài đặt cụthể.
?Làm như thếnào?
11
PHƯƠNG PH
PHƯƠNG PHÁ
ÁP TINH CH
P TINH CHỈ
ỈNH T
NH TỪ
ỪNG BƯ
NG BƯỚ
ỚC
C
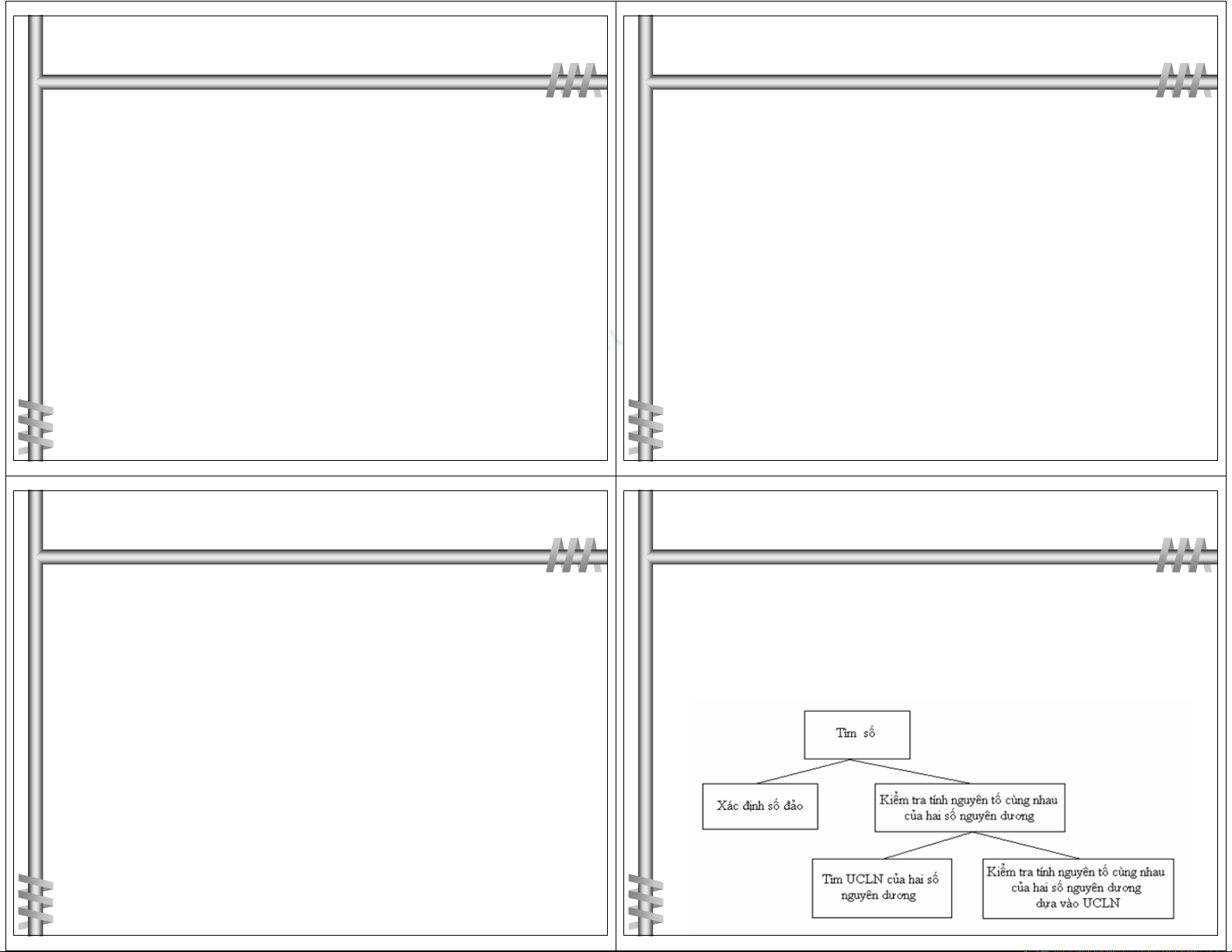
Bài toán: Tìm các sốcó 2 chữsốmà khi đảo trật tựcủa
hai số đósẽ được một sốnguyên tốcùng nhau với số
đã cho.
Bước 0:
12
PHƯƠNG PH
PHƯƠNG PHÁ
ÁP TINH CH
P TINH CHỈ
ỈNH T
NH TỪ
ỪNG BƯ
NG BƯỚ
ỚC
C
Bước 1.
•Dữliệu vào:
•Dữliệu ra:
•Ý tưởng thuật toán:
–Tìm các sốtừ 10 đến 99 thoảmãn yêu cầu và ghi vào mảng S và n
là số lượng các sốtìm được.
–Hiển thịkết quảtừmảng S.
13
PHƯƠNG PH
PHƯƠNG PHÁ
ÁP TINH CH
P TINH CHỈ
ỈNH T
NH TỪ
ỪNG BƯ
NG BƯỚ
ỚC
C
Bước 2.
Function Tim
•Vào:
•Ra: mảng S và n
•Biến nguyên n lưu số lượng các sốtìm được
1. n := 0;
2. Với mỗi sốx trong [10..99],
Kiểm tra xem x có số đảo là nguyên tốcùng nhau hay không, nếu
đúng thì đưa x vào mảng S và n := n + 1;
14
PHƯƠNG PH
PHƯƠNG PHÁ
ÁP TINH CH
P TINH CHỈ
ỈNH T
NH TỪ
ỪNG BƯ
NG BƯỚ
ỚC
C
Bước 3. Hàm tìm số đảo
•Function Sodao
–Vào: x là số nguyên dương
–Ra: Số đảo của x
–Ý tưởng: Từx, lần lượt lấy các chữsốtừbên phải của x để tạo số
y từtrái sang phải.
1. Khởi đầu y:=0
2. Với x> 0, lặp quá trình lấy chữsốhàng đơn vịcủa x bổsung
vào bên phải y
Tính y := y * 10 + (x mod 10) rồi x := x div 10
3. Trảvềsố đảo là y
15
PHƯƠNG PH
PHƯƠNG PHÁ
ÁP TINH CH
P TINH CHỈ
ỈNH T
NH TỪ
ỪNG BƯ
NG BƯỚ
ỚC
C
Bước 4. Kiểm tra xem x và số đảo của nó có nguyên tố
cùng nhau hay không
Function NTCN
•Vào: x là số nguyên dương
•Ra: True, nếu x và số đảo nguyên tốcùng nhau
False, nếu ngược lại.
•Ý tưởng: x là nguyên tốcùng nhau với số đảo của x khi và chỉ
khi UCLN(x, Sodao(x)) = 1.
if UCLN(x, Sodao(x)) = 1 then Return True
else Return False;
16
PHƯƠNG PH
PHƯƠNG PHÁ
ÁP TINH CH
P TINH CHỈ
ỈNH T
NH TỪ
ỪNG BƯ
NG BƯỚ
ỚC
C
Bước 5. Tìm UCLN của hai số nguyên dương: Thuật toán Euclid
•Function UCLN
•Vào: m, n nguyên (m >= n>= 0)
•Ra: UCLN là ước chung lớn nhất của m,n
•Biến r là số nguyên dương
1. Nếu m>n thì chuyển sang bước 2, ngược lại, hoán chuyển giá trịcủa m và
n.
2. Nếu n bằng 0 thì trảvềUCLN = m và kết thúc thuật toán
Ngược lại, chuyển sang bước 4.
3. Tính r là phần dư của phép chia m cho n.
4. Gán giá trịcủa n cho m và của r cho n. Quay lại bước 2.
17
PHƯƠNG PH
PHƯƠNG PHÁ
ÁP TINH CH
P TINH CHỈ
ỈNH T
NH TỪ
ỪNG BƯ
NG BƯỚ
ỚC
C
Bước 6.
•Hàm tìm UCLN
Function UCLN(a,b: integer) : integer;
Var r: integer;
Begin
If m < n then
Begin r := m; m := n; n := r; end;
While n > 0 do
Begin
r := m MOD n;
m := n; n := r;
end;
UCLN := m;
End;
18
PHƯƠNG PH
PHƯƠNG PHÁ
ÁP TINH CH
P TINH CHỈ
ỈNH T
NH TỪ
ỪNG BƯ
NG BƯỚ
ỚC
C
•Function Sodao(x: integer): integer;
Var y: integer;
Begin
y := 0;
while x > 0 do
begin
y := 10*y + (x MOD 10);
x := x DIV 10;
end;
Sodao := y;
End;
19
PHƯƠNG PH
PHƯƠNG PHÁ
ÁP TINH CH
P TINH CHỈ
ỈNH T
NH TỪ
ỪNG BƯ
NG BƯỚ
ỚC
C
•Function NTCN (x: integer): Boolean;
Begin
If UCLN(x, Sodao(x)) = 1 then NTCN := True
Else NTCN := false;
End;