Lý Thuyết Đàn Hồi
36
Chương III
LÝ THUYẾT BIẾN DẠNG
Dưới tác dụng của các lực ngoài, vật thể đàn hồi thay đổi hình dáng. Sự thay đổi hình dáng này có
thể định lượng thông qua chuyển vị của các điểm vật chất của vật thể. Giả thuyết liên tục (the continuum
hypothesis) tạo cơ sở cho sự tồn tại của một trường chuyển vị trong vật thể đàn hồi. Mỗi trường chuyển vị
tương ứng với một trường biến dạng xác định. Mục đích của chương này là đưa ra các định nghĩa cơ bản
của chuyển vị và biến dạng, xác lập các quan hệ giữa biến dạng và chuyển vị cũng như nghiên cứu các
yêu cầu bảo đảm tính liên tục và duy nhất của chuyển vị. Các quan hệ cơ bản của lý thuyết đàn hồi tuyến
tính được xây dựng trên cơ sở của lý thuyết biến dạng bé.
§3.1 Chuyển vị và biến dạng
Khảo sát vật thể đàn hồi dưới tác dụng của lực ngoài. Trước khi tác dụng lực, vật thể có cấu hình
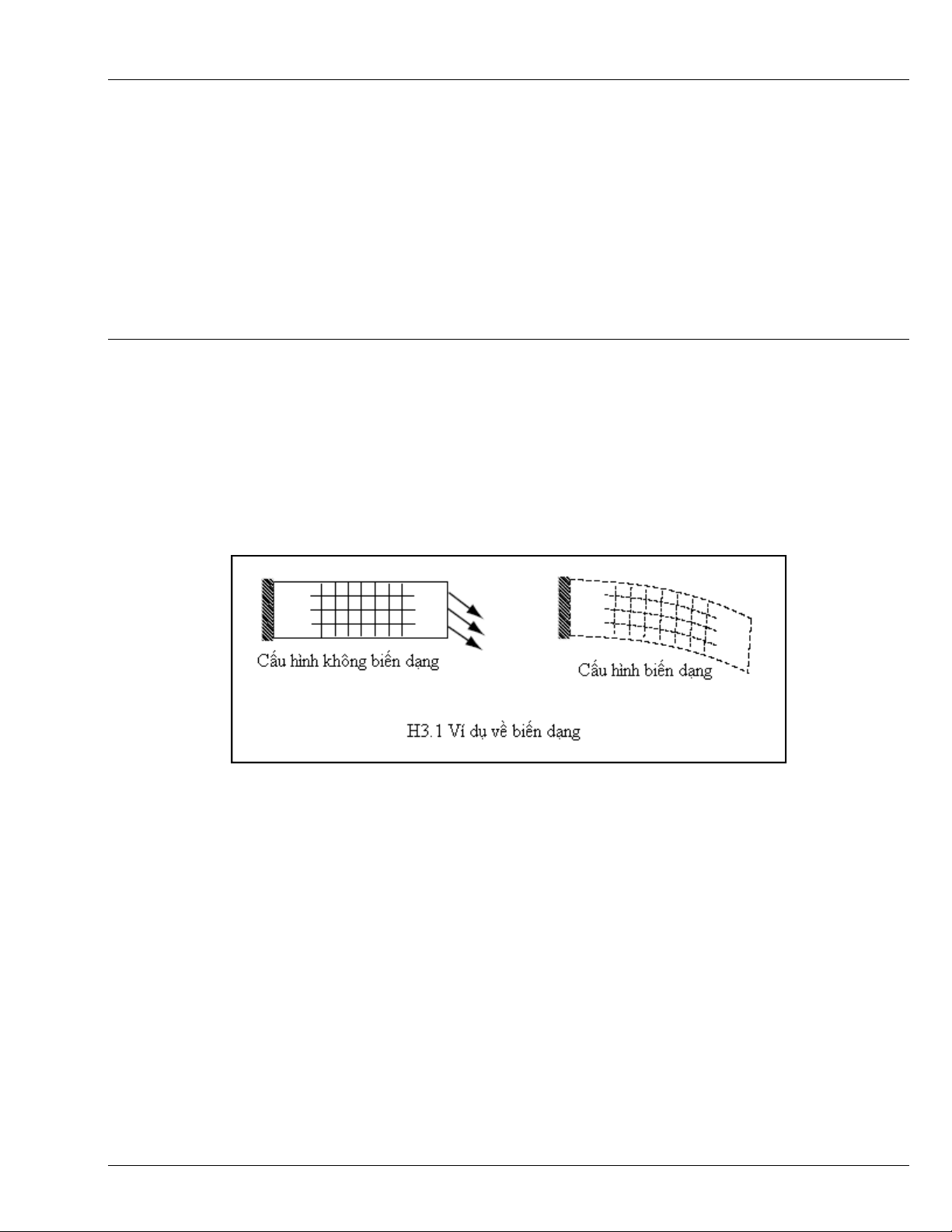
xác định. Sau khi chịu lực tác dụng, cấu hình vật thể thay đổi chút ít. Lấy minh họa từ trường hợp dầm
conson chịu tác dụng của các lực ngoài (H3.1 biểu thị): Cấu hình không biến dạng thể hiện ở lưới hình
chữ nhật, bên trái. Tác dụng của lực ngoài làm cho các điểm của dầm di chuyển, khiến cho dầm biến dạng,
như trên hình vẽ. So sánh các hình chữ nhật con trong hai cấu hình cho thấy cách thức mà các phân tố bên
trong vật thể biến dạng: chúng bị căng và bị lệch dạng (trượt). Biến dạng của vật thể đàn hồi phát sinh là
do có chuyển vị tương đối giữa các điểm bên trong vật thể. Chuyển vị loại này tương phản với chuyển vị
rắn, là chuyển vị bảo toàn khoảng cách giữa hai điểm của vật thể.
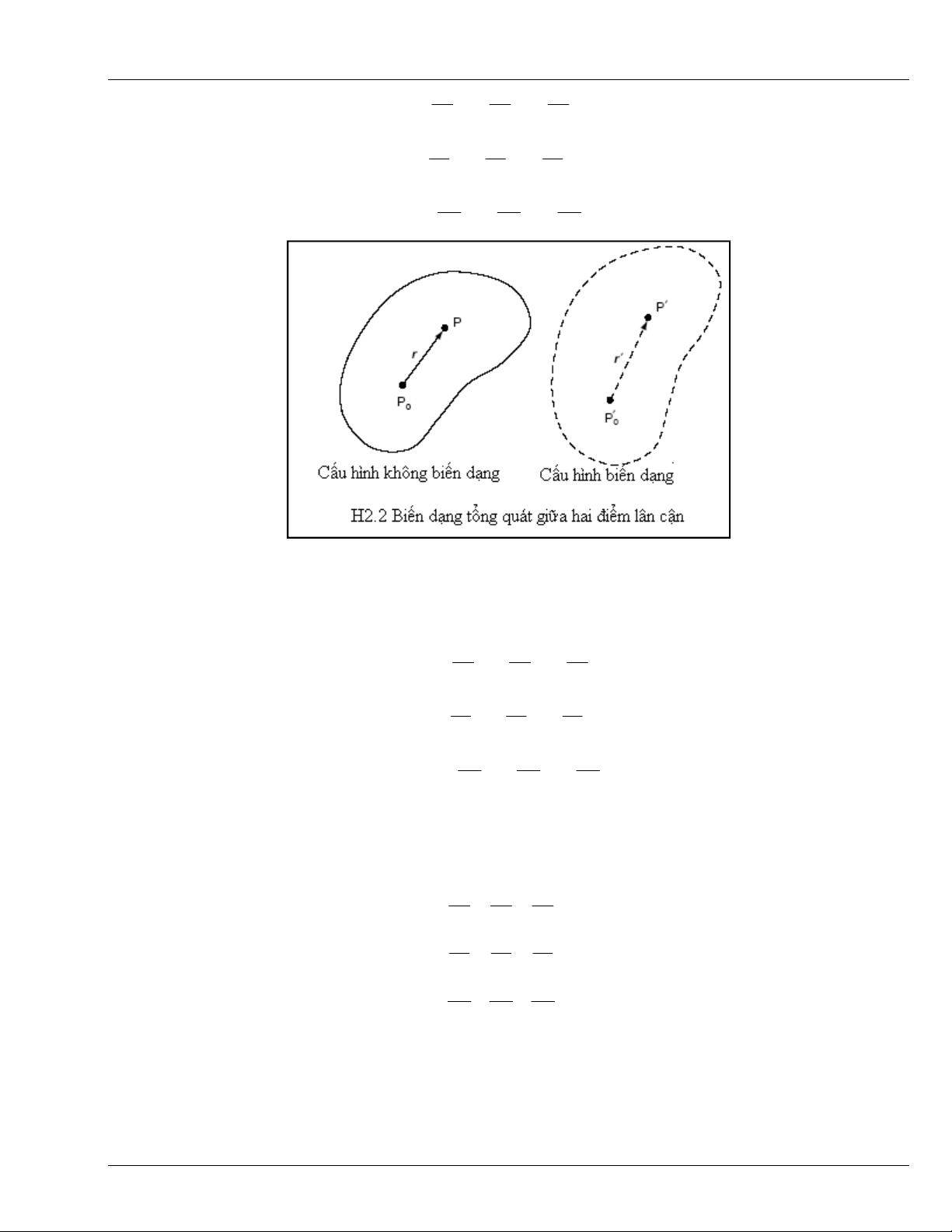
Để định lượng biến dạng, hãy xét hình H3.2. Trong cấu hình không biến dạng, chú ý đến hai điểm
P
0
và P cạnh nhau, xác định vector định vị tương đối r. Trong cấu hình biến dạng, các điểm này chiếm các
vị trí
'
0
P
và
'
P
. Trong lý thuyết biến dạng lớn/ hữu hạn, sự sai khác giữa cấu hình không biến dạng và cấu
hình biến dạng là đối tượng xem xét. Tuy nhiên, trong phạm vi của lý thuyết đàn hồi truyến tính, ta chỉ sử
dụng lý thuyết biến dạng bé, nên sự sai khác giữa cấu hình không biến dạng và cấu hình biến dạng được
bỏ qua. Sử dụng hệ tọa độ Đề-Các và định nghĩa vector chuyển vị tương đối của các điểm P
0
và P, tương
ứng, bởi u
0
và u.
Chuyển vị của các điểm trong vật thể đàn
hồi là hàm liên tục của các tọa độ, do đó, chuyển vị
) , ,( wvur
của điểm P lân cận với điểm P
0
có thể xác
định qua chuyển vị ),,(
0000
wvu ucủa điểm P
0
nhờ khai triển Taylor, bỏ qua các số hạng bậc cao vì các
thành phần của
r
là bé:
Lý Thuyết Đàn Hồi
37
.
;
;
0
0
0
zyx
zyx
zyx
r
z
w
r
y
w
r
x
w
ww
r
z
v
r
y
v
r
x
v
vv
r
z
u
r
y
u
r
x
u
uu
∂
∂
+
∂
∂
+
∂
∂
+=
∂
∂
+
∂
∂
+
∂
∂
+=
∂
∂
+
∂
∂
+
∂
∂
+=
(3.1)
S
ự
thay
đổ
i c
ủ
a vector v
ị
đị
nh t
ươ
ng
đố
i
(
((
(
)
))
)
zyx
rrr
,,r
do bi
ế
n d
ạ
ng
đượ
c xác
đị
nh b
ở
i
0
uurr'r −
−−
−=
==
=−
−−
−=
==
=∆
.
T
ừ
đ
ó,
.
;
;
0
0
0
zyxz
zyxy
zyxx
r
z
w
r
y
w
r
x
w
wwr
r
z
v
r
y
v
r
x
v
vvr
r
z
u
r
y
u
r
x
u
uur
∂
∂
+
∂
∂
+
∂
∂
=−=∆
∂
∂
+
∂
∂
+
∂
∂
=−=∆
∂
∂
+
∂
∂
+
∂
∂
=−=∆
(3.2)
Có th
ể
vi
ế
t (3.2) g
ọ
n h
ơ
n, d
ướ
i d
ạ
ng ký hi
ệ
u ch
ỉ
s
ố
:
jjii
r
ru
,
=∆
. (3.3)
Tensor
ji
u
,
có tên là tensor gradient chuy
ể
n v
ị
và có th
ể
đượ
c vi
ế
t d
ướ
i d
ạ
ng
∂
∂
∂
∂
∂
∂∂
∂
∂
∂
∂
∂∂
∂
∂
∂
∂
∂
=
z
w
y
w
x
w
z
v
y
v
x
v
y
u
y
u
x
u
ji ,
u
. (3.4)
Trên c
ơ
s
ở
các phép tính tensor, có th
ể
phân tích tensor gradient chuy
ể
n v
ị
thành t
ổ
ng c
ủ
a hai thành ph
ầ
n
đố
i x
ứ
ng và ph
ả
n x
ứ
ng nh
ư
sau
ijijji
ωeu +=
,
, (3.5)
trong đó,
Lý Thuyết Đàn Hồi
38
(
((
(
)
))
)
.
2
1
,, ijjiij
uue +
++
+=
==
=
; (3.6)
(
((
(
)
))
)
ijjiij ,,
2
1uuω−
−−
−=
==
=
(3.7)
Tensor
ij
e
được gọi là tensor biến dạng còn tensor
ij
ω
là tensor xoay.
Như vậy là theo lý thuyết biến dạng bé, sự thay đổi của vector vị trí tương đối giữa các điểm lân cận
nhau có thể biểu diễn dưới dạng tổng của các thành phần biến dạng và các thành phần xoay. Với việc
chọn chuyển vị
ii
dx≡r, trên cơ sở của các công thức (3.3) và (3.5) có thể biểu diễn dưới dạng tổng quát
jijjijii
dxdx ωeuu +
++
++
++
+=
==
=
0 . (3.8)
Chuyển vị kết quả trên bao gồm cả các biến dạng lẫn chuyển động - vật rắn. Để xác định phần chuyển
động - vật rắn, hãy sử dụng kết quả ở bài tập 1-13, trong đó, vector đối ngẫu (dual vector)
i
ω của tensor
xoay
ij
ω
được xác định bởi
jkijki
ωεω
2
1
−=
.
Nhờ đó tìm được
∂
∂
−
∂
∂
==
∂
∂
−
∂
∂
==
∂
∂
−
∂
∂
==
2
1
1
2
213
2
3
3
1
132
3
2
2
3
321
2
1
;
2
1
;
2
1
x
u
x
u
x
u
x
u
x
u
x
u
ωω
ωω
ωω
(3.9)
Các thành phần của vertor trên biểu thị chuyển vị xoay-vật rắn của các phần tử quanh các trục tọa độ.
Các phương trình (3.9), xác định phần chuyển động-vật rắn, còn có thể biểu diễn cô đọng dưới dạng
vector như sau
(
uωX
∇
=
21
(3.10).
Các kết quả thu được trên đây cho thấy rằng biến dạng của vật thể được biểu thị qua tensor biến dạng
ij
e
,
còn tensor này lại được tính theo gradient chuyển vị. Điều này xác lập mối quan hệ giữa các thành phần
của tensor biến dạng với các yếu tố hình học của chuyển vị của các điểm trên vật thể.
§3.2 Lý thuyết biến dạng bé
Các biến đàn hồi và các phương trình là những trường được định nghĩa tại từng điểm trong môi
trường liên tục. Tuy nhiên, việc xác lập các phương trình thường bắt đầu bằng việc khảo sát dáng điệu của
một phân tố có các cạnh vô cùng ngắn, sau đó, bằng kỹ thuật qua giới hạn, co phân tố về một điểm. Theo
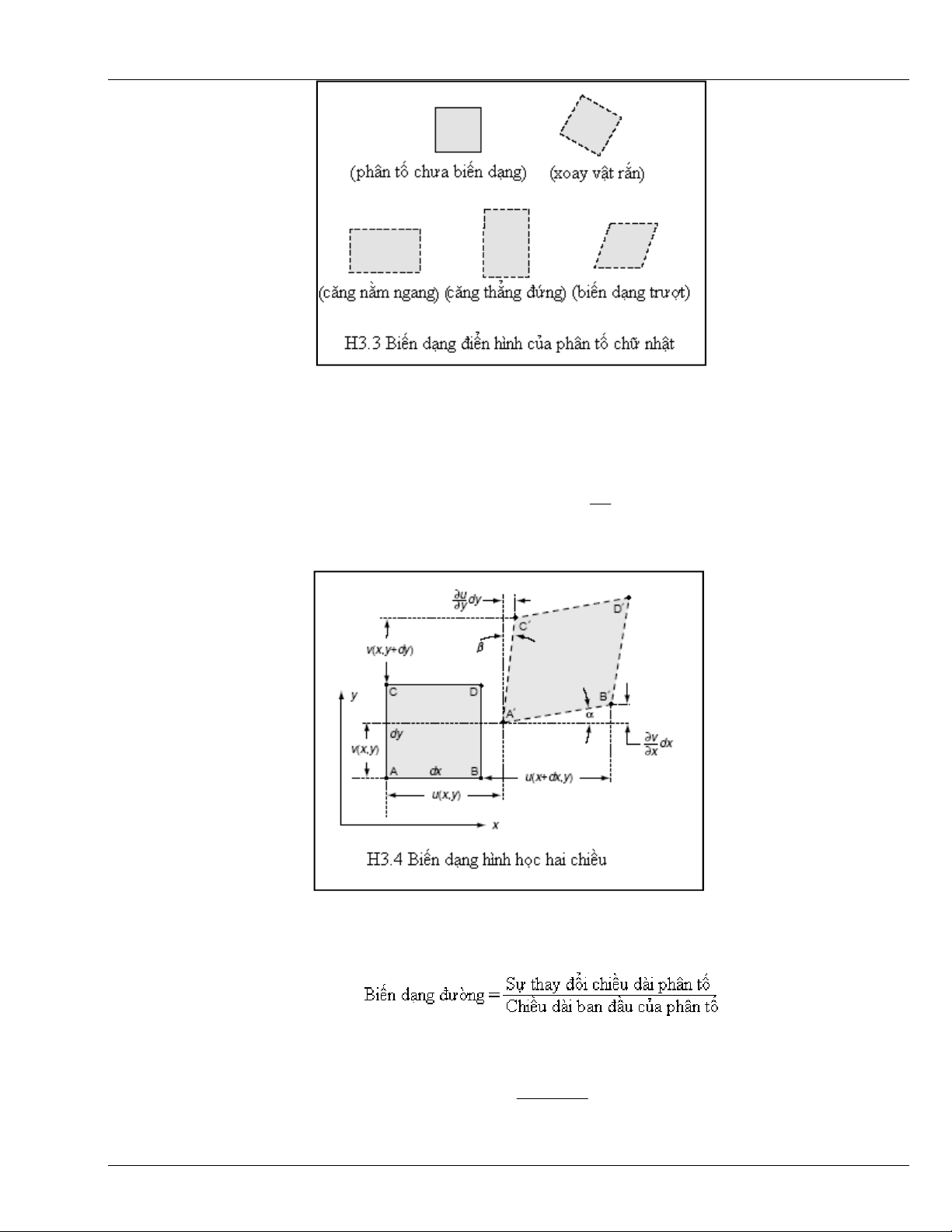
cách này, ta khảo sát biến dạng của một phân tố hình chữ nhật, như trên hình H3.3.
Chuyển vị tổng hợp của phân tố bao gồm:
• chuyển vị xoay vật rắn,
• biến dạng căng và
• biến dạng cắt,
như minh họa trên hình vẽ.
Chuyển động vật rắn không tham gia vào trường biến dạng, và do đó, chúng không có ảnh hưởng
đến ứng suất. Vì thế, ta chỉ tập trung vào biến dạng căng và biến dạng trượt.
Lý Thuyết Đàn Hồi
39
Hình 3.4 minh họa trợ giúp cho việc định lượng các biến dạng nói trên. Vị trí ban đầu (chưa biến
dạng) là ABCD còn vị trí sau biến dạng là A’B’C’D’. Tọa độ của điểm A là (x, y). Tọa độ của điểm B là
(x, y+dy), … .Các thành phần chuyển vị tại điểm bất kỳ là hàm liên tục của các tọa độ điểm này. Chẳng
hạn, các thành phần chuyển vị của điểm A:
(
)
yxvvyxuu
AA
,;,
=
=
. Theo lý thuyết biến dạng bé, các
thành phần chuyển vị của điểm B có thể tính theo dạng khai triển Taylor, bỏ qua các số hạng bậc cao:
( ) ( )
dx
x
u
yxuydxxuu
B
∂
∂
+=+= ,,
.
Tương tự như vậy cho thành phần còn laị cũng như cho các thành phần của các điểm còn lại.
Thành phần biến dạng dạng đường (hay biến dạng căng, biến dạng pháp tuyến), theo phương n,
được định nghĩa là sự thay đổi chiều dài trên một đơn vị chiều dài của một sợi vật chất theo phương n.
Biến dạng pháp đường là dương khi chiều dài của sợi dài ra, là âm khi ngắn lại. Trên hình H3.4, có
thể xác định biến dạng pháp tuyến tại điểm A theo phương x như sau
AB
ABBA
x
−
=''
ε
.
Cũng với những ký hiệu trên hình H3.4, tính được
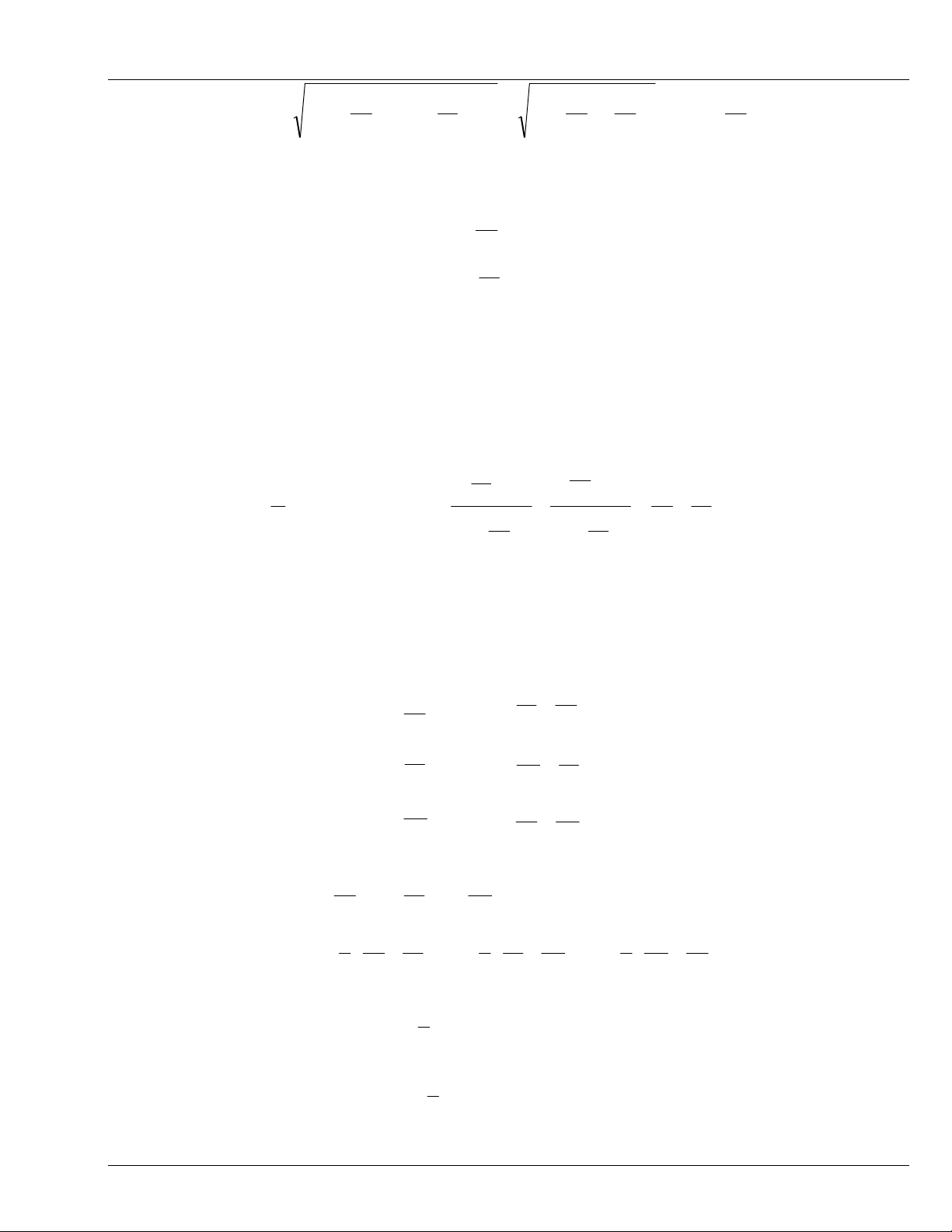
Lý Thuyết Đàn Hồi
40
dx
x
u
dx
x
u
x
u
dx
x
v
dx
x
u
dxBA
∂
∂
+≈
∂
∂
+
∂
∂
+=
∂
∂
+
∂
∂
+= 121''
222
trong
đ
ó các s
ố
h
ạ
ng b
ậ
c cao
đượ
c b
ỏ
qua, d
ự
a trên lý thuy
ế
t bi
ế
n d
ạ
ng bé.
V
ớ
i AB = dx, có th
ể
tính
đượ
c bi
ế
n d
ạ
ng pháp tuy
ế
n theo ph
ươ
ng x. C
ũ
ng ti
ế
n hành t
ươ
ng t
ự
theo ph
ươ
ng
y. K
ế
t qu
ả
, thu
đượ
c:
x
u
x
∂
∂∂
∂
∂
∂∂
∂
=
==
=
ε
(3.11)
y
v
y
∂
∂∂
∂
∂
∂∂
∂
=
==
=
ε
(3.12)
Thành ph
ầ
n bi
ế
n d
ạ
ng th
ứ
hai, bi
ế
n d
ạ
ng c
ắ
t hay còn g
ọ
i bi
ế
n d
ạ
ng tr
ượ
t
đượ
c
đị
nh ngh
ĩ
a là s
ự
thay
đổ
i c
ủ
a góc gi
ữ
a hai h
ướ
ng v
ố
n vuông góc nhau trên v
ậ
t th
ể
. M
ộ
t cách chính xác,
đ
ây là
đị
nh ngh
ĩ
a bi
ế
n
d
ạ
ng c
ắ
t k
ỹ
thu
ậ
t. Trong lý thuy
ế
t
đ
àn h
ồ
i, nh
ằ
m m
ụ
c
đ
ích tensor hóa cách th
ứ
c trình bày, bi
ế
n d
ạ
ng c
ắ
t
đượ
c
đị
nh ngh
ĩ
a b
ằ
ng m
ộ
t n
ử
a, (1/2), s
ự
thay
đổ
i góc gi
ữ
a hai tr
ụ
c vuông góc nhau [xem công th
ứ
c (3.7)].
Đơ
n v
ị
đ
o bi
ế
n d
ạ
ng c
ắ
t là radian. Bi
ế
n d
ạ
ng c
ắ
t là d
ươ
ng khi góc gi
ữ
a hai h
ướ
ng d
ươ
ng c
ủ
a hai tr
ụ
c
gi
ả
m, âm khi ng
ượ
c l
ạ
i. V
ậ
y là d
ấ
u c
ủ
a bi
ế
n d
ạ
ng c
ắ
t ph
ụ
thu
ộ
c vào h
ệ
t
ọ
a
độ
trong khi d
ấ
u c
ủ
a bi
ế
n d
ạ
ng
đườ
ng là
độ
c l
ậ
p. Nh
ư
trên hình H3.4, bi
ế
n d
ạ
ng c
ắ
t k
ỹ
thu
ậ
t có th
ể
xác
đị
nh b
ở
i
x
v
y
u
dy
y
v
dy
dy
y
u
dx
x
u
dx
dx
x
v
BAC
xy
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
≈+=∠−=
βα
π
γ
'''
2 (3.13)
trong quá trình bi
ế
n
đổ
i
đ
ã s
ử
d
ụ
ng các quan h
ệ
g
ầ
n
đ
úng trên:
β
β
α
α
tan ,tan
≈
≈
và các s
ố
h
ạ
ng b
ậ
c
cao trong gradient c
ũ
ng
đượ
c b
ỏ
qua, d
ự
a trên c
ơ
s
ở
gi
ả
thi
ế
t bi
ế
n d
ạ
ng bé. L
ư
u ý th
ấ
y r
ằ
ng, các
đạ
o hàm
riêng trên
đ
ây là d
ươ
ng khi các c
ạ
nh AB và AC xoay vào trong, nh
ư
trên H3.4. N
ế
u nh
ư
, ch
ỉ
đơ
n gi
ả
n,
đổ
i
ch
ỗ
hai tr
ụ
c x và y c
ũ
ng nh
ư
u và v, bi
ế
n d
ạ
ng c
ắ
t là không
đổ
i, t
ứ
c
yxxy
γγ
=
. Trong tr
ườ
ng h
ợ
p 3D, c
ũ
ng
b
ằ
ng các l
ậ
p lu
ậ
n và tính toán t
ươ
ng t
ự
nh
ư
đ
ã làm trên
đ
ây, ta thu
đượ
c các k
ế
t qu
ả
t
ổ
ng quát sau:
;
;
;
z
w
y
v
x
u
z
y
x
∂
∂
=
∂
∂
=
∂
∂
=
ε
ε
ε
.
;
;
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
=
x
w
z
u
z
v
y
w
y
u
x
v
zx
yz
xy
γ
γ
γ
(3.14)
S
ử
dung ký hi
ệ
u ch
ỉ
s
ố
(tensor), có th
ể
bi
ể
u di
ễ
n các quan h
ệ
trên d
ướ
i d
ạ
ng
∂
∂∂
∂
∂
∂∂
∂
+
++
+
∂
∂∂
∂
∂
∂∂
∂
=
==
=
∂
∂∂
∂
∂
∂∂
∂
−
−−
−
∂
∂∂
∂
∂
∂∂
∂
=
==
=
∂
∂∂
∂
∂
∂∂
∂
−
−−
−
∂
∂∂
∂
∂
∂∂
∂
=
==
=
∂
∂∂
∂
∂
∂∂
∂
=
==
=
∂
∂∂
∂
∂
∂∂
∂
=
==
=
∂
∂∂
∂
∂
∂∂
∂
=
==
=
z
u
x
w
e
y
w
z
v
e
x
v
y
u
e
z
w
e
y
v
e
x
u
e
zxyzxy
zyx
2
1
,
2
1
,
2
1
;,,
hay d
ướ
i d
ạ
ng tensor:
)
ijjiij ,,
2
1uue +=
, (3.15)
trong khi n
ế
u s
ử
d
ụ
ng cách vi
ế
t d
ướ
i d
ạ
ng vector/ma tr
ậ
n, có
( )
[
]
T
uue ∇+∇=
2
1
. (3.16)