
www.truongthi.com.vn Lớp học qua mạng
Bài 14 - MẠCH XOAY CHIỀU CÓ R, L, C (TIẾP)
A- Trả lời các câu hỏi kỳ trước:
1- Có phảI khi cộng hưởng thì UL, UC đều cực đại?
- Như bài trước ta đã nhận xét: để tạo ra cộng hưởng, phải làm
cho ZL=ZC 1
LC
ω
ω
⇒= do đó có 3 cách tạo ra cộng hưởng.
+ Nếu thay đổi L, giữ nguyên C và
ω
thì ZC không đổi do đó khi
cộng hưởng thì axmCC
Z
UIZ⇒=cũng đạt cực đạI còn
.
L
Z
L
ω
=bị thay đổi theo L do đó UL=IZL nói chung không đạt cực
đại lực cộng hưởng
+ Tương tự: nếu thay đổi C, giữ nguyên L và
ω
thì khi cộng hưởng
UL=IZL sẽ đạt cực đại còn UC=IZC nói chung không cực đại.
+ Nếu giữ nguyên L, C mà thay đổI
ω
thì cộng hưởng I max còn
ZL, ZC đều bị thay đổI nên nói chung cũng không đạt cực đại.
- UL và UC lúc cộng hưởng không nhất thiết phải lớn hơn U
chung. Quan hệ giữa UL, UC v à U lúc cộng hưởng còn tuỳ thuộc
giá trị của R với ZL, ZC do đầu bài cho.
2- Có trường hợp nào I khi cộng hưởng lại gần bằng I lúc bình thường ko?
Trường hợp này có thể xảy ra nếu điện trở thuần R của mạch lớn hơn
nhiều so với ZL,ZClúcchưacộnghưởng.
Ví dụ: Mạch R, L, C nối tiếp có U=100V, R= 400
Ω
; ZL=60 ; ZΩC=20
Ω
.
Thay đổi L để xảy ra cộng hưởng: so sánh IC lúc đầu với I lúc cộng
hưởng. - Ban đầu:
()
2
2
400 60 402Z20
=
+− ≈Ω
120 0, 2985
402
U
I
A
Z
== ≈
- Khi cộng hưởng: max max
120
I0,3
400
UAI
RI
=
== ⇒=
-
UI . Hiện tượng này gọi là cộng
hưởng tù.
ax ax . 0,3.20 6 120
Cm m C
Z VU===<<=V
Môn Vật Lý Thầy giáo Đỗ Lệnh Điện
Trường PTTH Hà Nội – Amsterdam.
www.truongthi.com.vn Lớp học qua mạng
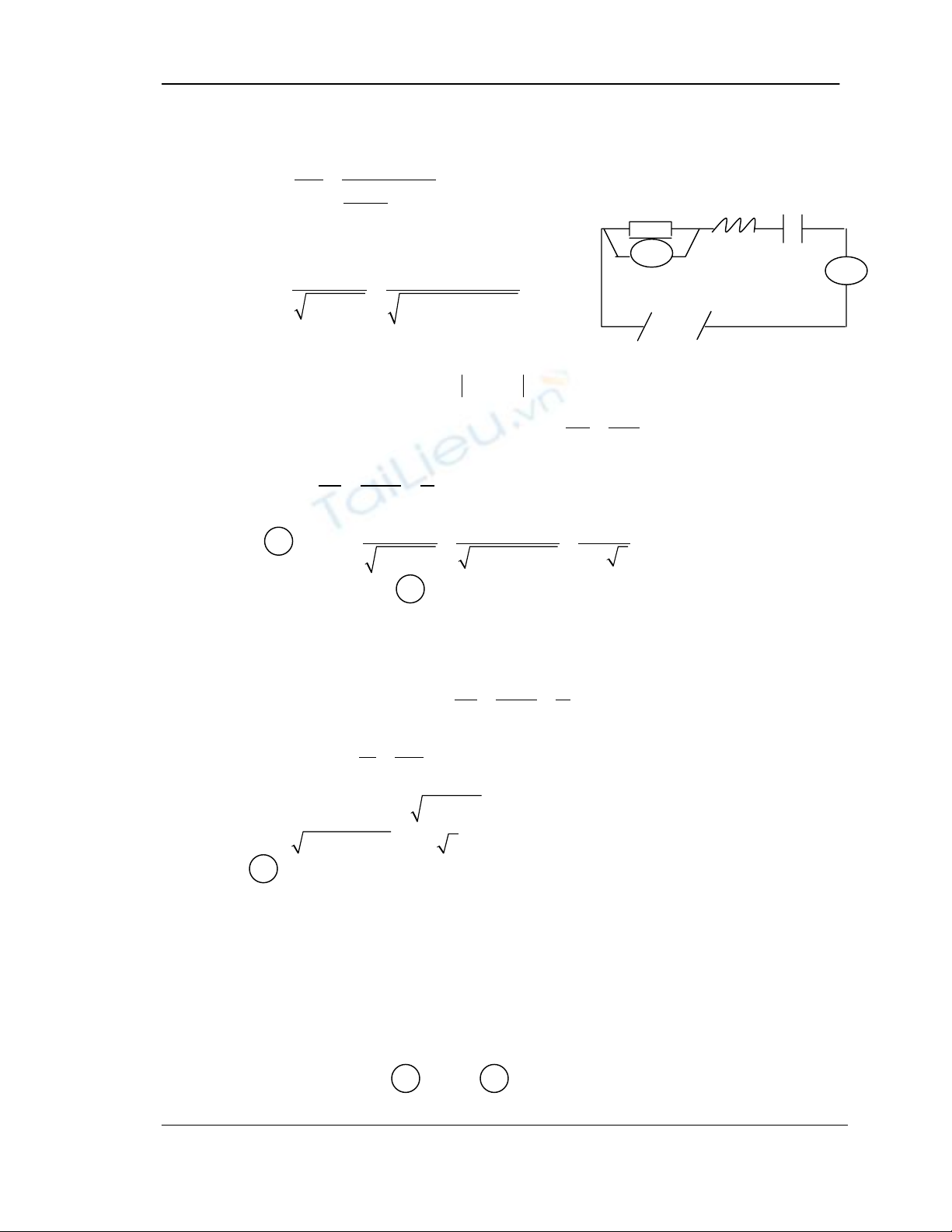
B- Bài tập
11
200
10 4 .100
2
C
ZC
ωπ
π
== =
−Ω
L B
RC
V
U ∼
A
A
a- Tính L và số chỉ Ampe
-
()
22 2
AB
LLC
UU
IRZ RZZ
==
++−2
Theo giả thiết: UAB =U=120V
()
()
2
2
200
2 100
22
LLC LLC
C
LLC LCL
ZZZ ZZZ
Z
ZZZ ZZZ
⇒= − ⇒=−
⇒=− − ⇔ =⇔= = =Ω
Vậy 100 1
100
L
Z
LH
ω
ππ
== =
- chủ 22 2 2
120 120 0,54
100 5
200 100
AB
L
U
I
A
RZ
== =≈
++
A
b- Tính L và số chỉ khi UC max
V
Từ UC=I . ZC => khi thay đổi L và ZC không đổi => UC max
Khi Imax => xảy ra cộng hưởng.
200 2
200 100
L
LC
Z
Z
ZL H
ω
ππ
⇒== Ω⇒= = =
Lúc này Imax = 120 1, 2
100
UA
R==
22
max max
22
.
1, 2 100 200 120 5 268,3
AB AB L
UIZIRZ
V
==+
=+==
chỉ 268,3V
V
B- Bài giảng: Giải bài toán dòng điện xoay chiều bằng cách lập hệ nhiều
phương trình.
1- Nguyên tắc: Nếu trong mạch xoay chiều ta đã biết tất cả các số liệu về R,
L, C và biết hiệu điện thế U đặt vào mạch thì chúng ta sẽ tách được tất cả
các đại lượng trong mạch như I, U, P…
Nếu có 1 trong các đại lượng trên chưa biết thì đầu bài phải cho thêm một
điều kiện bổ sung n số chỉ , số chỉ , góc lệch pha
ϕ
….
hư
A
V
Môn Vật Lý Thầy giáo Đỗ Lệnh Điện
Trường PTTH Hà Nội – Amsterdam.
www.truongthi.com.vn Lớp học qua mạng
Số điều kiện cho thêm phải đúng bằng số đại lượng còn thiếu thì bài toán
mới đủ điều kiện để giải.
2- Cách giải: Sử dụng các điều kiện đầu bài đã cho để lập hệ phương trình.
Số phương trình cần lập phải đúng bằng số ẩn còn thiếu.
U
R
A
C
D
B
L
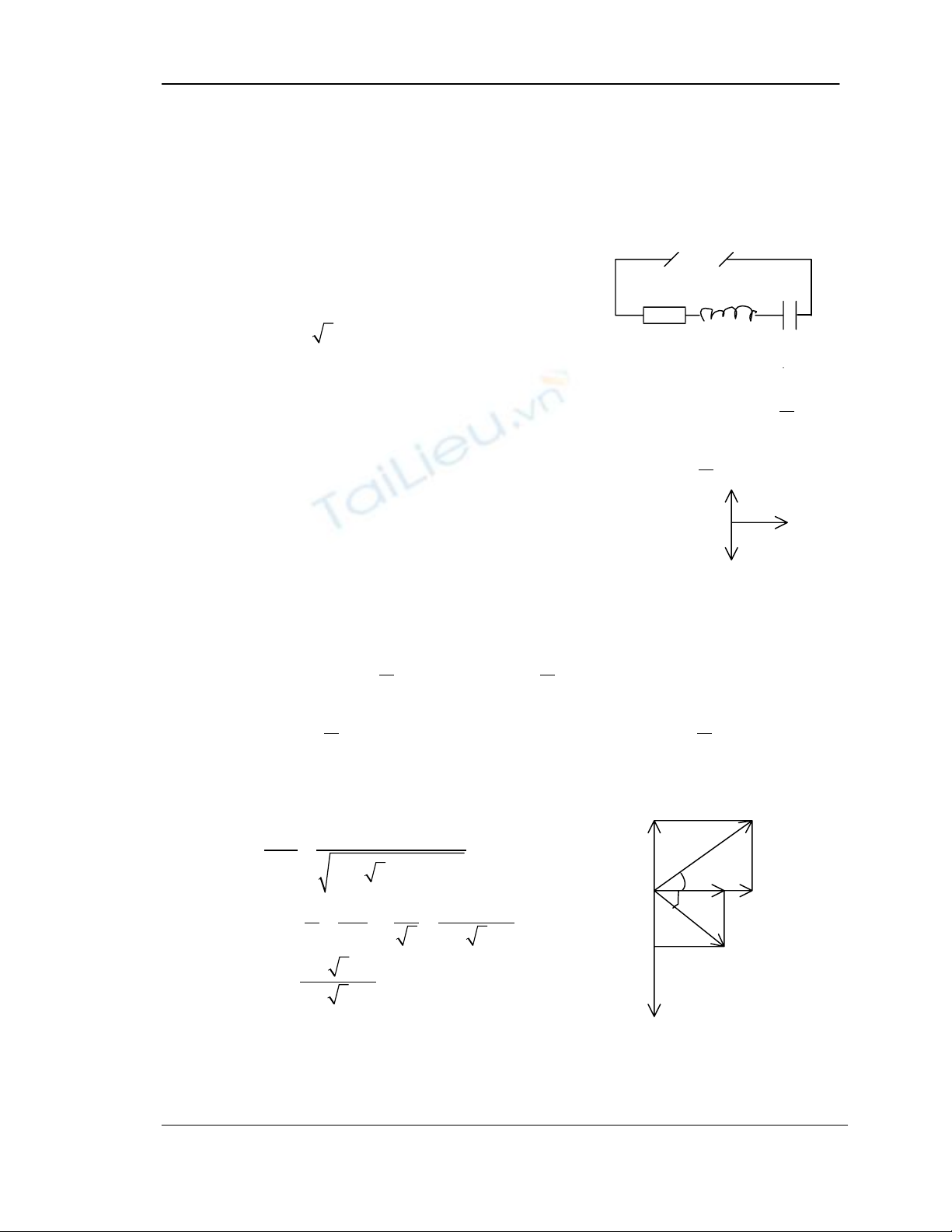
Ví dụ 1: Cho mạch điện như hình vẽ
U=U0sin100 t
π
(V)
100 3R=Ω
Dùng vôn kế có điện trở rất lớn:
- Mắc vào A,C thì vôn kế chỉ 200V và mắc vào UAC sớm pha hơn i: 6
π
C
- Mắc vào B, D thì vôn kế chỉ 173,2V và UBD trễ pha hơn i: 3
π
a- Chứng minh rằng cuộn dây có điện trở r
b- Tính r, L, C và U0
c- Viết biểu thức của i và của U ở hai đầu cuộn dây
GIẢI
a- Chứng minh cuộn dây có r: Giả sử cuộn dây không có điện trở. Khi đó UL
sớm pha hơn i: 2
π
. UC trễ pha hơn i: 2
π
=> UL ngược pha với UC => UBD sẽ
lệch pha 2
π
so với i => trái với giả thiết là lệch pha so với i: 3
π
. Vậy cuộn
dây phải có r
UAC
2
ϕ
1
ϕ
Ur
""#
L
U
"
"#
Rr
U
"""#
BD
U
""""#
C
U
"""#
I
#
C
U
"""#
L
U
""#
b- Tính r, L, C, U0
-
()
22
1
200 (1)
100 3
1
63 100 3
100 3 (2)
3
AC
AC L
LL
Br
L
U
IZrZ
UZ
tg Ur
r
Z
π
==
++
⇒=
tg
ϕ
==
+
+
⇔=
Môn Vật Lý Thầy giáo Đỗ Lệnh Điện
Trường PTTH Hà Nội – Amsterdam.

www.truongthi.com.vn Lớp học qua mạng
Thay (2) vào (1) ta có:
() ()
2
2
200 200 3 (3)
100 3 .2
100 3
100 3 3
Ir
r
r
==
+
+
++
-
()
2
2
100 3 (4)
BD
BD CL
U
ZrZZ+−
I== . Theo giả thiết UBD trễ pha hơn i => ZC > ZL
2
r
33
3
CL CL CL
UU ZZ
tg tg Z Z r
Ur (5)
π
ϕ
−−
== ⇒= ⇔−=
Thay (5) vào (4):
()
2
2
100 3 100 3 (6)
2
3
Ir
rr
==
+
Từ (3) và (6): 200 3 100 3 2 100 3 100 3
2
2(100 3 )
Irr
r
r
==⇔=+⇔=
+rΩ
- Từ (2):
100 3 100 3 100 3 200
33
200 2
100
L
L
r
Z
Z
LH
ωππ
++
== =
== =
Ω
- Từ (5):
5
3 3.100 3 300
300 300 200 500
112
.10
500.100
CL
CL
C
ZZ r
CF
Z
ω
ππ
−
−= = = Ω
=+=+=Ω
⇒= = =
ZZ
- Từ (6):
()( )
()
()
2
22
00
100 3 100 3 0,5
22.100 3
200 3 500 200
100 12 9 100 21
0,5 2.100 21 50 42 648
CL
IA
r
rZZ
UIZ V
== =
=++− = +−
=+=Ω
== = $
2
ZR
c- Viết biểu thức i và UBC
- 020,52
I
IA==
Môn Vật Lý Thầy giáo Đỗ Lệnh Điện
Trường PTTH Hà Nội – Amsterdam.
www.truongthi.com.vn Lớp học qua mạng
Góc lệch pha giữa U và i là
ϕ
200 500 300 3
2
100 3 100 3 200 3
0,714
LC
ZZ
tg Rr
rad
ϕ
ϕ
−−−
== ==
++
⇒=−
−
ϕ
<0 chứng tỏ U trễ pha hơn i => i sớm pha hơn U
Vậy 0,5 2 sin(100 0,714)
π
=+it A
- Hiệu điện thế ở hai đầu cuộn dây
()
2
22 2
0
r
r 0,5 100 3 200
0,5.100 3 4 50 7
2 50 14 187
200 2
' ' 0,857
100 3 3
BC L
BC BC
LL
UI Z
UU V
UZ
tg Ur
ϕϕ
=+= +
=+=
==
=== =⇒=
$
BC
U
U
"
#
ϕ
I
UC
URr
Ur
UL
=> UBC sớm pha hơn U ' 0,857 0,714 1,571 2
π
ϕϕ
+= + = $
Vậy 187 sin 100 2
BC
π
π
=+
Ut V
BÀI TẬP VỀ NHÀ
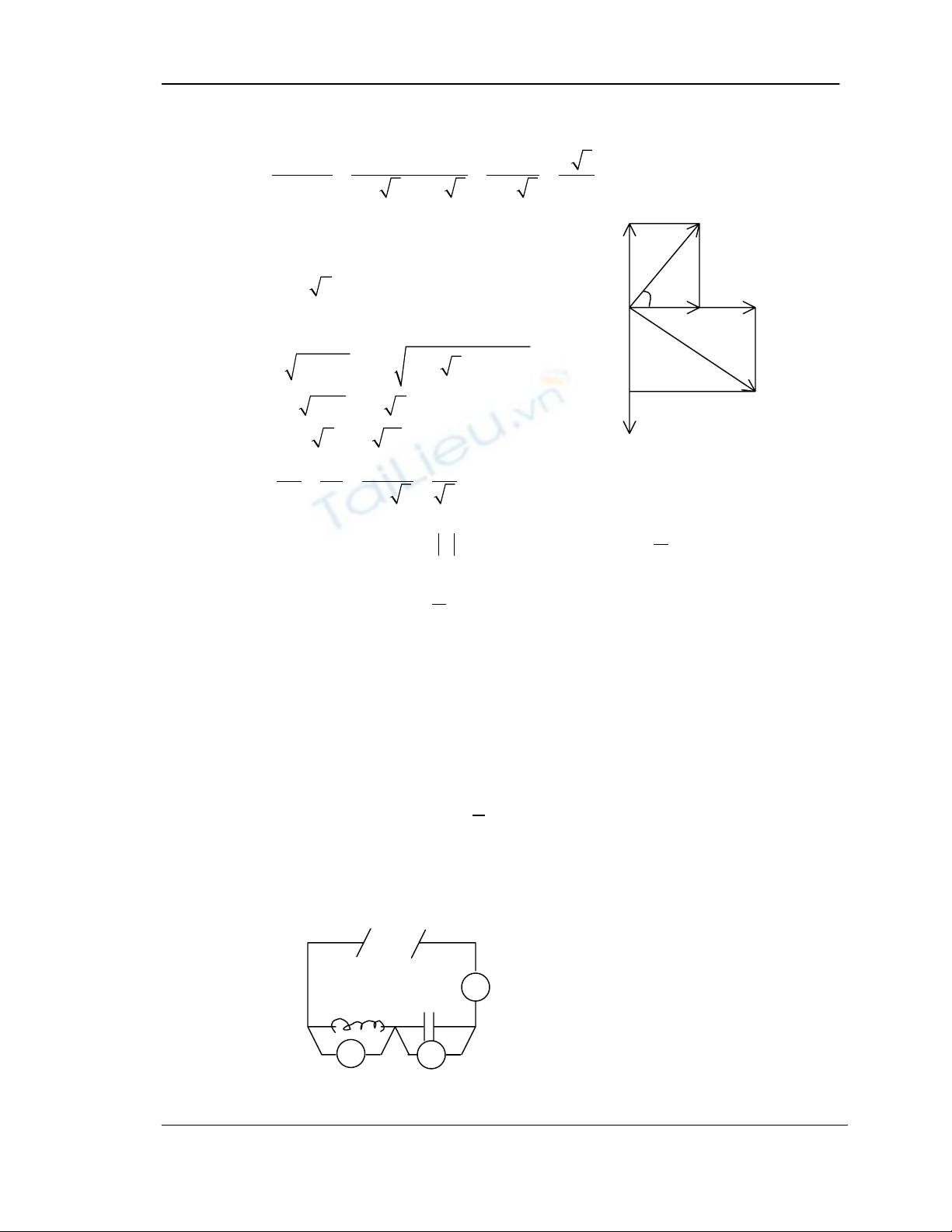
1- Cho mạch điẹn như hình vẽ. Các vôn kế có điện trở rất lớn, ampe kế có điện
trở không đáng kể. Am pe kế chỉ 0,4A, vôn kế 1 chỉ 100V, vôn kế 2 chỉ 48V. UAB
sớm pha hơn i góc 1
ϕ
với 1
4
3
ϕ
tg
=
a- Tính R, ZL, ZC và U
b- Thay đổi f đến giá trị 100 Hz thì ZL=10Zc. Tính L, C và f0 ban đầu.
U∼
A
V2
V1
Môn Vật Lý Thầy giáo Đỗ Lệnh Điện
Trường PTTH Hà Nội – Amsterdam.


























