MÔ HÌNH HOÁ ĐỘNG CƠ KHÔNG ĐỒNG BỘ MỘT PHA
CÓ MỘT VÒNG NGẮN MẠCH
MODELING SINGLE PHASE INDUCTION MOTORS WITH ONE SHORTED
SHADING LOOP ON THE POLE
TRẦN VĂN CHÍNH
Trường Đại học Bách khoa, Đại học Đà Nẵng
TÓM TẮT
Bài báo trình bày kết quả xây dựng mô hình toán học của động cơ không đồng bộ một pha
mở máy bằng vòng ngắn mạch với giả thiết mạch từ của máy không bão hoà. Trên cơ sở mô
hình toán học này, một sơ đồ mô phỏng dựa trên phần mềm Matlab được xây dựng. Từ kết
quả mô phỏng có thể nhận thấy ảnh hưởng của các thông số của vòng ngắn mạch đến đặc
tính làm việc của động cơ. Trên cơ sở đó có thể hiệu chỉnh vòng ngắn mạch để đạt được đặc
tính động cơ mong muốn.
ABSTRACT
This paper shows the mathematical model of induction motors with one shorted shading loop
on the pole. The simulation schema is developed on the basis of the model. The impact of the
short-circuit shading loop on the motor characterictics is derived from the simulation results.
The parameters of the short-circuit shading loop will be corrected to attain the desirable
characteristics of motors.
1. Giới thiệu
Động cơ không đồng bộ một pha được dùng nhiều trong các thiết bị điện gia đình. Để
có thể tạo ra mô men quay, các động cơ loại này hoặc có cuộn dây phụ nối với tụ điện hoặc có
vòng ngắn mạch đặt trên cực từ. Loại động cơ thứ hai thường được dùng nhiều trong các máy
có công suất nhỏ do kết cấu đơn giản. Trong [1], các công thức tính toán thông số được trình
bày. Tuy nhiên khó dùng chúng để hiệu chỉnh động cơ nhằm đạt được tính năng mong muốn.
Việc mô hình hoá động cơ là một cách cho phép nhận được quan hệ giữa đặc tính làm việc
của động cơ và các thông số của vòng ngắn mạch. Các thông số này sẽ được thay đổi cho đến
khi nhận được đặc tính làm việc tốt nhất. Việc xây dựng mô hình toán học và sơ đồ mô phỏng
các dạng động cơ khác [2], [3], [4] được chú ý nhiều do tính phổ biến của chúng. Riêng mô
hình của động cơ một pha có vòng ngắn mạch còn ít được chú ý đến. Đây là một vấn đề có
tính ứng dụng cao vì phương pháp này giúp cho việc tối ưu hoá động cơ một pha có vòng
ngắn mạch được dễ dàng.
2. Xây dựng mô hình toán học
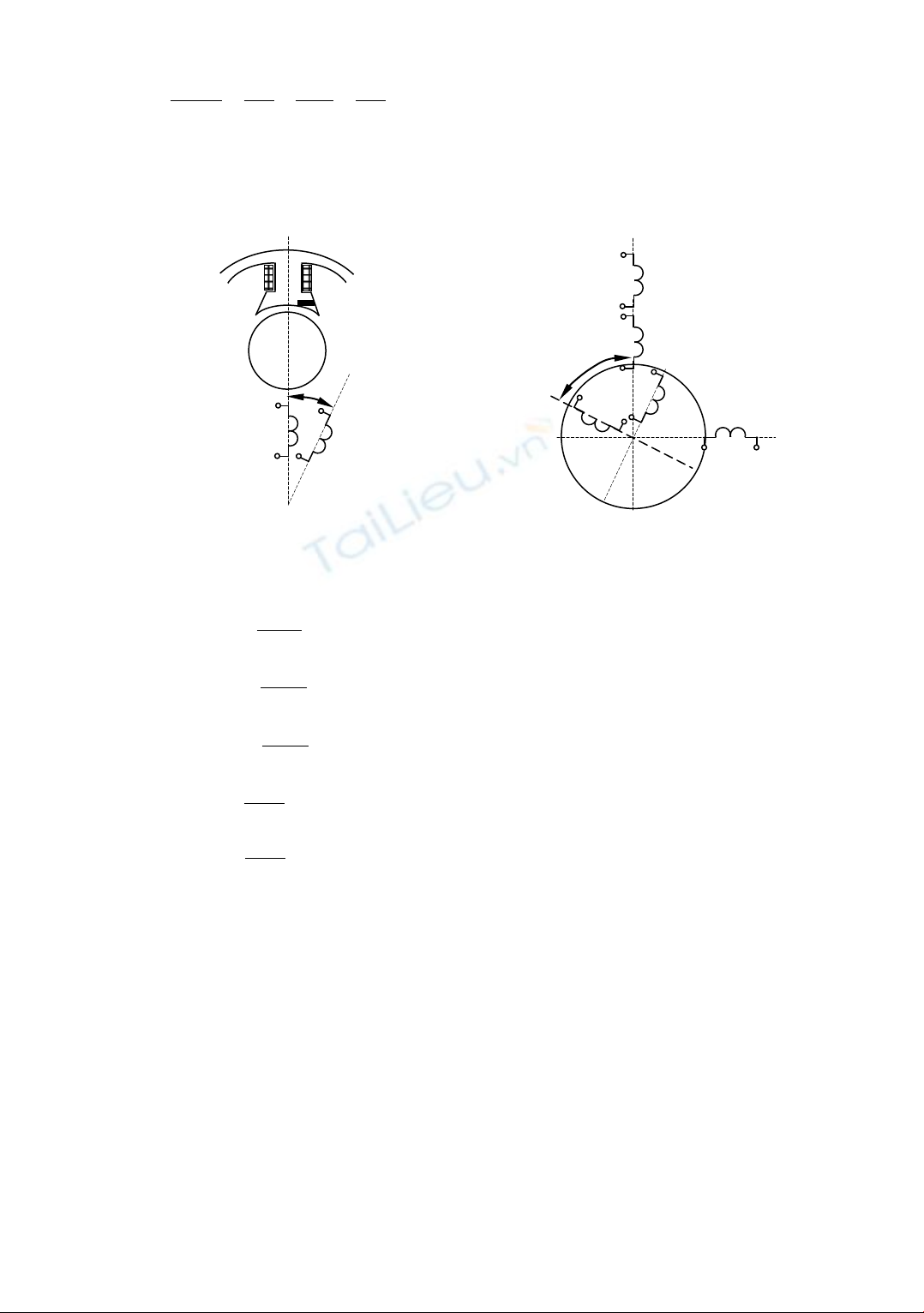
Các động cơ không đồng bộ một pha có một vòng ngắn mạch có cấu tạo khá đơn giản
nhưng mô tả toán học quá trình biến đổi năng lượng trong chúng tương đối phức tạp. Sơ đồ
cấu trúc của động cơ có một vòng ngắn mạch như hình 1. Mỗi cuộn dây tạo nên một từ trường
đập mạch và từ trường tổng trong khe hở không khí của máy là từ trường quay ellip. Từ
trường đập mạch của mỗi cuộn dây là tổng của hai từ trường quay thuận và nghịch theo hai
chiều ngược nhau. Ta phân tích cuộn dây ngắn mạch wB thành 2 cuộn dây vuông góc với
nhau là wBcos và cuộn dây wBsin. Các dây quấn roto đối xứng (hình 2). Mô hình này không
đối xứng cả về điện từ lẫn không gian. Cuộn dây wB có 1 vòng dây và hệ số dây quấn kB = 1.
Cuộn dây wA có hệ số dây quấn kA = 1. Như vậy hệ số quy đổi từ dây quấn B sang dây quấn
A là:
Bb d
BB
A A A Aa q
MM
wk 1
kw k w M M
(1)
Từ (1) ta suy ra:
q
d
MM
M kM
(2)
Phương trình cân bằmg điện áp của các dây quấn là:





qs1
qs1 qs1 qs1
qs2
qs2 qs2 qs2
ds2
ds2 ds2 ds2
qr
qr qr qr
dr
dr dr dr
d
u i r dt
d
u i r dt
d
u i r dt
d
u i r dt
d
u i r dt
(3)
Trong đó:
wqs1 = wA wqs2 = wBcos wqs1 = wBsin
Từ thông móc vòng với các dây quấn có thể biểu diễn bởi các phương trình sau:
 







 


qs1 qs1qs1 qs1qs2 qs1qr qs1dr
qs2 qs1qs2 qs2qs2 qs2qr qs2dr
ds2ds2 ds2qr ds2dr
ds2
qrqs1 r qrqs2 qrds2 qrqr
qr
drqs1 r drqs2 drd
dr
L L 0 L cos L sin
L L 0 L cos L sin
0 0 L L sin L cos
L cos L cos L sin L 0
L sin L sin L

















qs1
qs2
ds2
qr
s2 drdr dr
i
i
i
i
cos 0 L i
(4)
Các hệ số trong (4) cho bởi:
2 2 2
qs1qs1 qs1 qs1 g c c g ds2ds2 f g
qs1qr qs1 r g c r g qs1dr qs1 r g
L L W L W L L cos cos
L W W W W L W W
A
w
Hình 1: Cấu trúc động cơ
d
Hình 2: Mô hình động cơ
A
w
B
w cos
q
B
w sin
qr
w
dr
w
ds2qr ds2 r g r g ds2dr r g
L W W sin W L sin W


22
qrqr r r g drdr r r g
qs1qs2 qs1 qs2 g c g
L L W L L W
L W W W cos
Do các phương trình trên được viết cho hệ toạ độ tự nhiên gắn với các trục dây quấn stato và
roto nên để chuyển về hệ toạ độ stato ta dùng các ma trận sau:







qd
cos sin
T ( ) sin cos




 

1
qd
r
cos sin
T ( ) sin cos
(5)
Áp dụng (2) và (5), sau khi biến đổi toạ độ và quy đổi từ các dây quấn về dây quấn chính wqs1
ta nhận được hệ phương trình đối với từ thông và điện áp như sau:

s
qs1 qs1 qs1 mq qs1 qs2 qr
s
qs2 qs2 qs2 mq qs1 qs2 qr
s
ds2 ds2 ds2 mq ds2 dr
s s s
qr r qr mq qs1 qs2 qr
ss
dr r dr mq ds2
L i L (i i cos i )
L i L (i sin i cos i )
L i L (i sin i )
L i L (i sin i sin i )
L i L (i sin i s
dr )
(6)



qs1
qs1 qs1 qs1
qs2
qs2 qs2 qs2
ds2
ds2 ds2 ds2
s
qr
s s s r
qr qr r dr
s
s s s dr
r
dr dr r qr
d
u i r dt
d
u i r dt
d
u i r dt
d
d
u i r dt dt
d
d
u i r dt dt
(7)
Mô men điện từ của động cơ được bằng tốc độ thay đổi năng lượng từ trường trong các cuộn
dây:
s s s s s s s
em qr dr dr qr mq dr qs1 dr qs2 qr ds
pp
M i i L (i i sin i i sin i i )
22
(8)
hay:
ss
em ds2 qs1 ds2 qs2 qs1 ds2 qs2 ds2
b
p
M ( i sin i sin i i )
2
(9)
Phương trình chuyển động của động cơ được viết là:

rm em co cd
rb em co cd
d
J M M M
dt
d( / )
2H M M M
dt
(10)
Mô phỏng
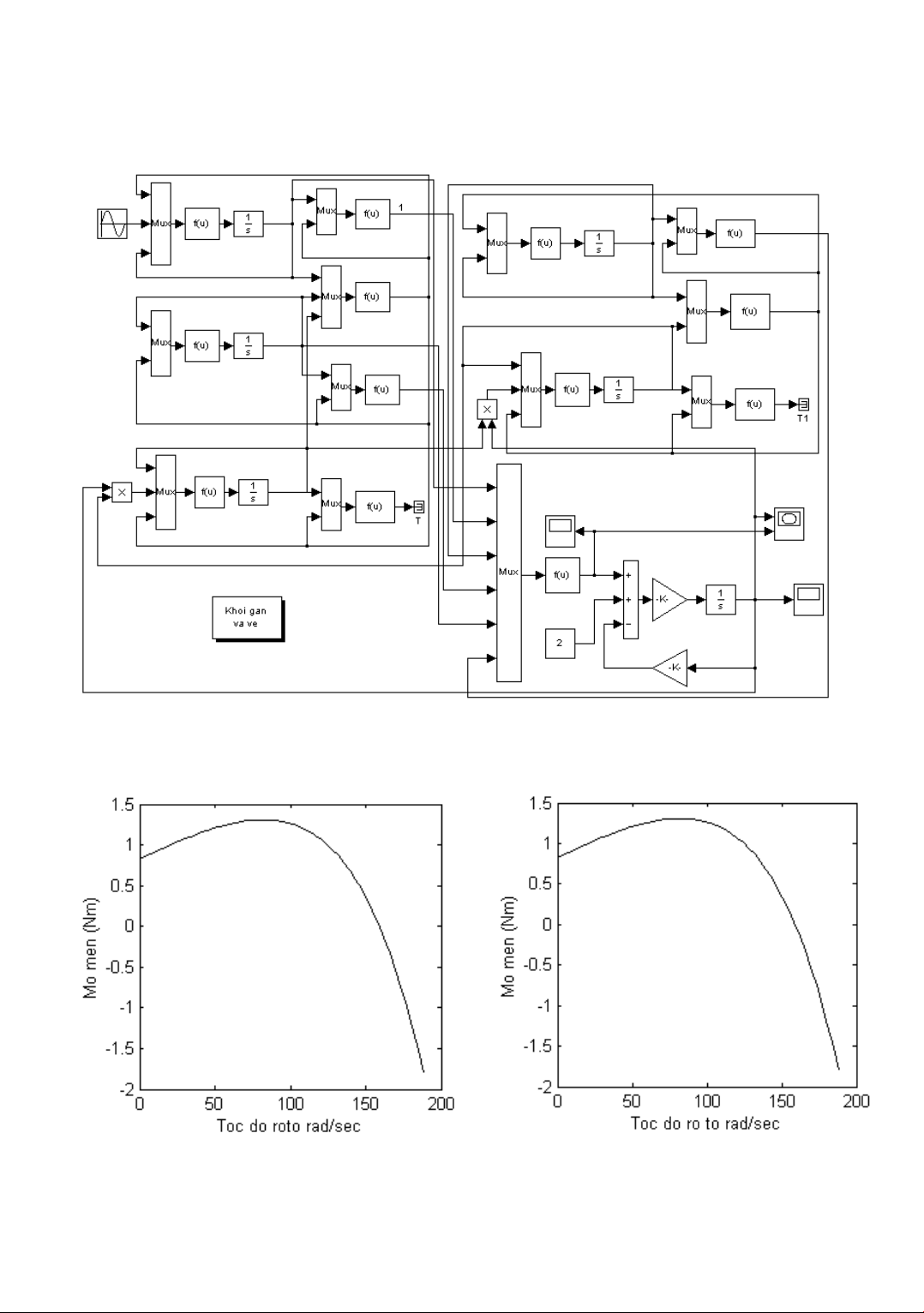
Sử dụng các phương trình (6) (10) ta xây dựng sơ đồ mô phỏng như hình 3:
Hình 3
Hình 4a
Hình 4b
Dùng sơ đồ này mô phỏng động cơ không đồng bộ một pha có một vòng ngắn mạch
có: P = 30W, U = 220V, xqs1 = 38,8, xqs2 = 26 , xmq = 104, rqs1 = 102, rqs2 =
48,3 ta nhận được đường cong mô men với các giá trị = 0.4 và = 0.55 như hình 4a và 4b.
4. Nhận xét và kết luận
Qua mô phỏng động cơ với các giá trị khác nhau ta nhận thấy đặc tính M() thay
đổi hầu như không đáng kể. Như vậy có nghĩa là vòng ngắn mạch chỉ có tác dụng tạo ra mô
men quay và ít ảnh hưởng đến tham số của máy. Nguyên nhân do vòng ngắn mạch thường chỉ
có thể chiếm một phần nhỏ của cực từ và từ thông qua đó thường không lớn. Khi tăng điện trở
của vòng ngắn mạch, mô men có xu hướng giảm nhưng không nhiều.
Trong quá trình mở máy, mô men của động cơ dao động nhiều khi lớn và giảm đi
khi ta giảm . Nguyên nhân là do khi tăng, điện kháng của vòng ngắn mạch tăng lên nên
dao động dòng điện tăng lên và dao động mô men cũng tăng lên.
TÀI LIỆU THAM KHẢO
[1] E.M.Lopukhina, G.X. Comikhina, Rastriot asynschronus microdvigachenlei
odnophasei triphase toca, Gosudastvenoie energitreskoie izdachelstbo, Moskva, 1961.
[2] W.N. Fu. P. Zou, D.Lin, S. Stanton, Z. J. Cendes, Modeling of Solid Conductors in
Two – Dimensional Transient Finite-Element Analysis and Its Application to Electric
Machines.
[3] Herbert De Gersem. Karen De Brabandere, Ronnie J. M. Belmans, Motional Time-
Harmonic Simulation of Slotted Single-Phase Induction Machines.
[4] Yosuke Nakagawa, Kenjiro Takemure, Takashi Maeno, The Frictional
Characteristics of Single-phase-drive type USM.
[5] Hamit A. Tolyat, Shailesh P. Waikar, Thomas A. Lipo, Analysis and Simulation of
Five Phase Synchronous Reluctance Machines Including Third Harmonic of Airgap
MMF.
[6] Kopylov. I. P. Mathematical Models of Electrical Machines, Mir Publishers, Moscow,
1984.