Ch ng 2ươ
Phân tích m ch đi n hình sin xác l pạ ệ ậ
Tóm t t lý thuy tắ ế
ch đ hình sin xác l p nh có bi n đ i ph c mà đi n áp c a m t nhánh g m 3Ở ế ộ ậ ờ ế ổ ứ ệ ủ ộ ồ
thông s m c n i ti p Rố ắ ố ế k, Lk, Ck là
∫
++= dti
C
1
dt
di
LiRu k
k
k
kkkk
tr thànhở
mk
k
mk
CkLkk
mk
k
kk
.
IZ
.
I)ZZR(
.
I)
Cj
LjR( =++=
ω
+ω+ 1
(2.1)
Nh v y toán t nhánh hình th cư ậ ử ứ Lk=
∫
++ dt
Cdt
d
LR
k
kk
1
tr thành t ng tr ph c:ở ổ ở ứ
ZK=Rk+jωLk+
k
Cjω
1
(2.2)
và toán t nhánh đ o L ử ả -1k tr thành t ng d n ph c:ở ổ ẫ ứ
YK=1/Zk (2.3)
Vì v y h ph ng trình tr ng thái d dàng đ c vi t d ng ph c v i s thay thậ ệ ươ ạ ễ ượ ế ở ạ ứ ớ ự ế
t ng ng: u, i, eươ ứ →
...
m
.
m
.
m
.
E,I,UhoÆcE,I,U
; Lkk, Lkl→ Zkk, Zkl ; L -1kk, L -1kl→ Ykk, Ykl.
Đo n m ch đi n th ng đ c đ c tr ng b i t ng tr ph c ho c t ng d n ph c:ạ ạ ệ ườ ựơ ặ ư ở ổ ở ứ ặ ổ ẫ ứ
jbgY
jXR
I
U
I
U
Z
.
.
m
.
m
.
+
==+===
11
(2.4)
T ng quát thì R, X, g, b đ u là hàm c a bi n t n s . Đ d c tr ng cho s ph thu cổ ề ủ ế ầ ố ể ặ ư ự ụ ộ
vào t n s c a m ch ng i ta đ a ra đ c tính t n s thông qua hàm truy n đ t ph cầ ố ủ ạ ườ ư ặ ầ ố ề ạ ứ
T(jω)=IT(jω)Iejθ(ω), là t s c a bi u di n ph c c a ph n ng trên bi u di n ph c c a tácỷ ố ủ ể ễ ứ ủ ả ứ ể ễ ứ ủ
đ ng. Đ th IT(jộ ồ ị ω) I g i là đ c tính biên đ t n s , đ th ọ ặ ộ ầ ố ồ ị θ(ω) g i là đ c tính pha t n sọ ặ ầ ố
c a m ch đi n.ủ ạ ệ
C ng h ng là đ c tr ng quan tr ng c a m ch đi n hình sin. M ch c ng h ng khi Xộ ưở ặ ư ọ ủ ạ ệ ạ ộ ưở
ho c b=0. Gi i ph ng trình X ho c b=0 s xác đ nh đ c ặ ả ươ ặ ẽ ị ượ các t n s c ng h ng c aầ ố ộ ưở ủ
m ch. ạM ch RLC n i ti p và song song đ c đ c tr ng b i các tham s t ng k t trong b ngạ ố ế ượ ặ ư ở ố ổ ế ả
2.1
Khi có h c m thì đi n áp trên 1 cu n c m Lỗ ả ệ ộ ả k s có đi n áp t c m là jẽ ệ ự ả ωLk
mk
.
I
và các
đáp h c m ỗ ả
ml
kl
.
IMjω±
, t c ứ
. D u c a các đi n áp h c m xácấ ủ ệ ỗ ả
đ nh theo c c cùng tên: n u dòng ị ự ế
mk
.
I
và
ml
.
I
cùng h ng vào hay cùng r i các c c cùng tênướ ờ ự
c a hai cu n c m Lủ ộ ả k và Ll thì l y d u “+”, ng c l i - d u “-”.ấ ấ ượ ạ ấ
41
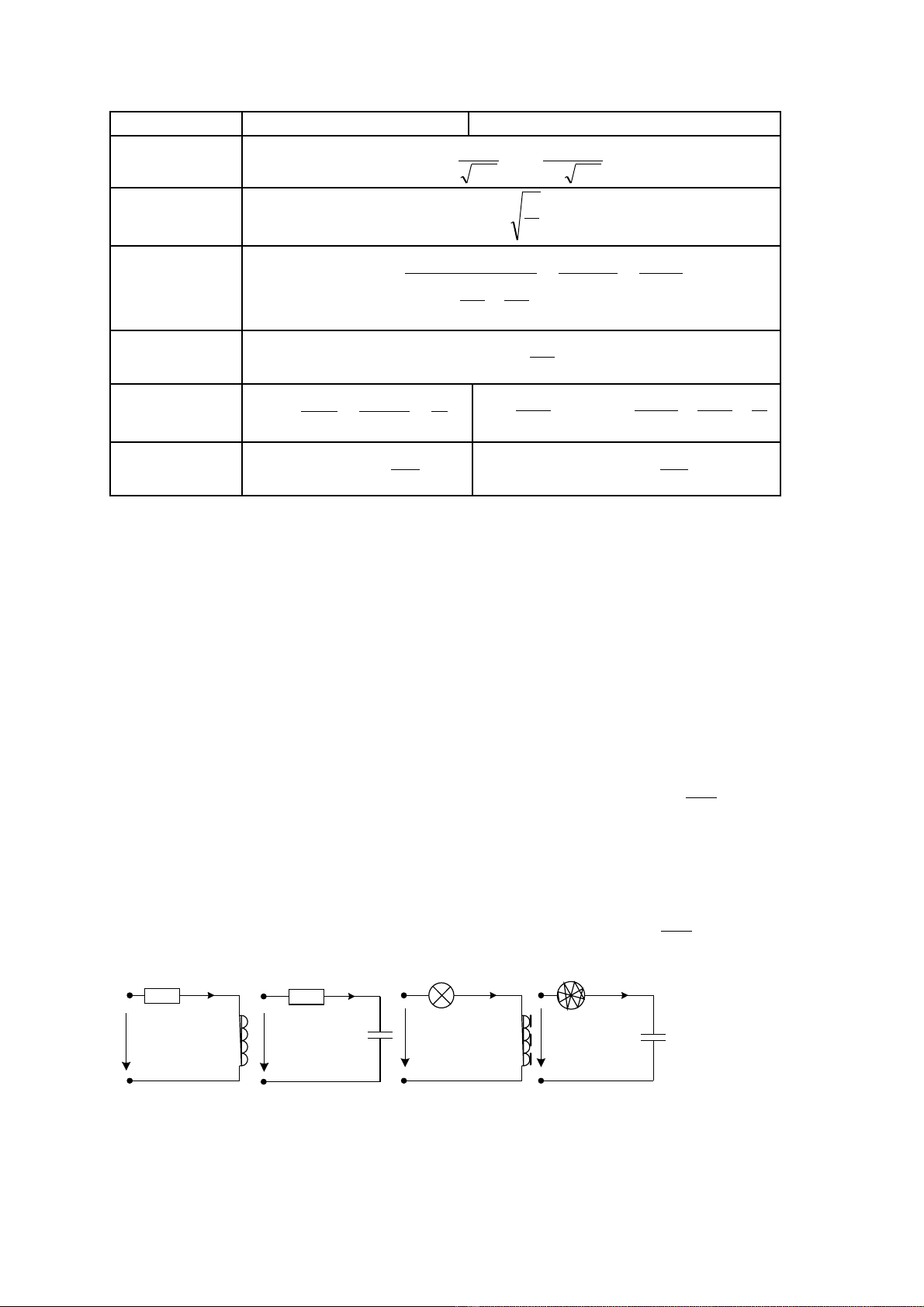
B ng2.1ả
Tham sốM ch RLC n i ti pạ ố ế M ch RLC song songạ
T n s c ngầ ố ộ
h ngưở
LC
f;
LC π
==ω 2
11
00
Tr khángở
sóng
C
L
=ρ
Hàm truy nề
đ t quyạ
chu nẩ
ξ+
=
ν+
=
ω
ω
−
ω
ω
+
=ω jjQ
)(jQ
)j(T
ˆ
1
1
1
1
1
1
0
0
D i thôngả
Q
,0
70
ω
=ω∆
H s ph mệ ố ẩ
ch tấ
RCRR
L
Qρ
=
ω
=
ω
=
0
01
ρ
=
ω
=
ω
=ω=
ω
=R
L
R
Lg
CR
g
C
Q
00
0
0
1
T ng tr ,ổ ở
t ng d n.ổ ẫ Z=R+j(
C
Lω
−ω 1
) Y=g+j(
L
Cω
−ω 1
)
BÀI T PẬ
2.1. Cho các đi n áp và dòng đi n:ệ ệ
1. u1(t)=220cos(2π.50t+250)[V] 2. u2(t)=60sin(108t+300)[mV]
3. i1(t)=1,25cos(2π.50t+250)[A] 4. i2(t)=100sin(1010t+0,785)[mA]
Hãy bi u di n các đi n áp và dòng đi n trên sang d ng:ể ễ ệ ệ ạ
a) Biên đ ph c. ộ ứ b) Hi u d ng ph c. ệ ụ ứ
2.2. Chuy n các dòng đi n ph c sau t d ng đ i s v d ng mũ:ể ệ ứ ừ ạ ạ ố ề ạ
]A[,jI.]A[,jI.
]A[,jI.]A[,jI.
m
.
m
.
m
.
m
.
88682548868253
88682528868251
43
21
−=−−=
+−=+=
2.3. Cho m ch đi n hình 2.1. Tìm hàm truy n đ t ph c d ng ạ ệ ề ạ ứ ạ
m
.
m
.
U
I
)j(T =ω
r i v đ c tínhồ ẽ ặ
biên đ t n s và đ c tính pha t n s t ng ng. Gi i thích t i sao khi t n s c c l n (ộ ầ ố ặ ầ ố ươ ứ ả ạ ầ ố ự ớ ω→∞)
thì đ c tính biên đ t n s ti n t i 0.ặ ộ ầ ố ế ớ
2.4. Cho m ch đi n hình 2.2. Tìm hàm truy n đ t ph c d ng ạ ệ ề ạ ứ ạ
m
.
m
.
U
I
)j(T =ω
r i vồ ẽ
H×nh 2.1
u(t)
i(t)
R
L
H×nh 2.2
u(t)
i(t)
R
C
H×nh 2.4
i(t)
C
qu¹ t
H×nh 2.3
L
bãng ®Ìn
220V
50Hz
220V
50Hz
đ c tính biên đ t n s và đ c tính pha t n s t ng ng. Gi i thích t i sao khi t n s b ngặ ộ ầ ố ặ ầ ố ươ ứ ả ạ ầ ố ằ
0 (ch đ m t chi u) thì đ c tính biên đ t n s ti n t i 0.ế ộ ộ ề ặ ộ ầ ố ế ớ
42
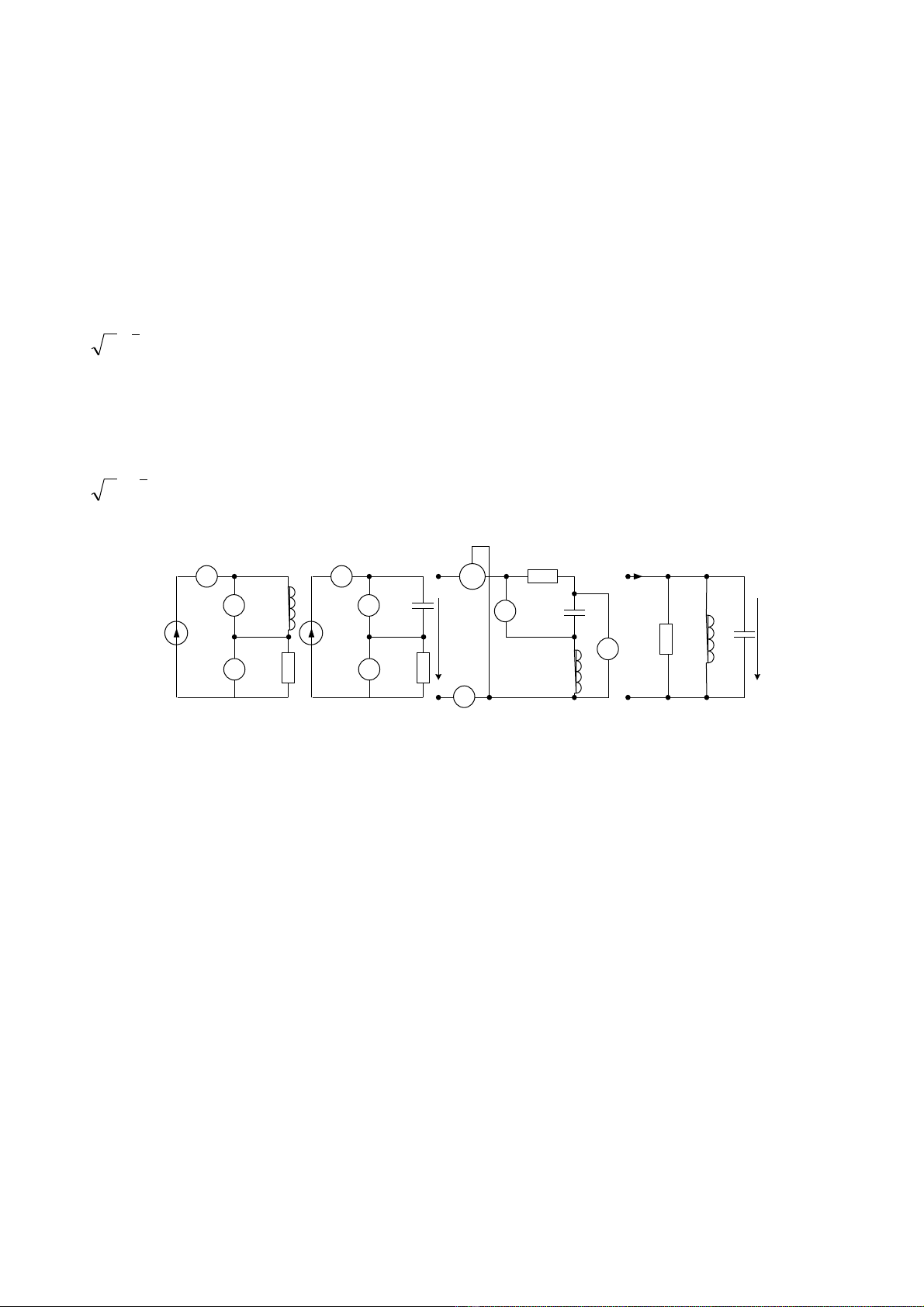
2.5. Trên m t bóng đi n th p sáng có ghi “80V-40W”. Nó đ c m c n i ti p v i m t cu nộ ệ ắ ượ ắ ố ế ớ ộ ộ
c m L vào m ng đi n 220V-50Hz nh hình 2.3. H i cu n c m L c n có tr s là bao nhiêuả ạ ệ ư ở ỏ ộ ả ầ ị ố
đ bóng đi n sáng bình th ng.ể ệ ườ
2.6. M t qu t đi n 110V-60W c n c m vào ngu n 220V-50Hz. Đ qu t không b cháy ph iộ ạ ệ ầ ắ ồ ể ạ ị ả
m c n i ti p qu t v i m t t C nh hình 2.4. H i t C c n có tr s là bao nhiêu đ qu tắ ố ế ạ ớ ộ ụ ư ở ỏ ụ ầ ị ố ể ạ
làm vi c bình th ng n u coi qu t nh m t đi n tr thu n tiêu tán công su t 60W. ệ ườ ế ạ ư ộ ệ ở ầ ấ
2.7. Xác đ nh ịchỉ s c a các d ng c đo (lý t ng) cho m ch đi n hình 2.5 trong hai tr ngố ủ ụ ụ ưở ạ ệ ườ
h p:ợ
a) Ngu n tác đ ng là hình sin có giá tr hi u d ng U=10V, bi t t ng tr ph c c a m ch là Z=ồ ộ ị ệ ụ ế ổ ở ứ ủ ạ
4
2
π
j
e
b) Ngu n tác đ ng là m t chi u Uồ ộ ộ ề 0=10V.
2.8. Xác đ nh ch s ị ỉ ố c aủ các d ng c đo (lý t ng) cho m ch đi n hình 2.6 trong hai tr ngụ ụ ưở ạ ệ ườ
h p:ợ
a) Ngu n tác đ ng là hình sin có giá tr hi u d ng U=10V, bi t t ng tr ph c c a m ch là Z=ồ ộ ị ệ ụ ế ổ ở ứ ủ ạ
4
2
π
−j
e
b) Ngu n tác đ ng là m t chi u Uồ ộ ộ ề 0=10V.
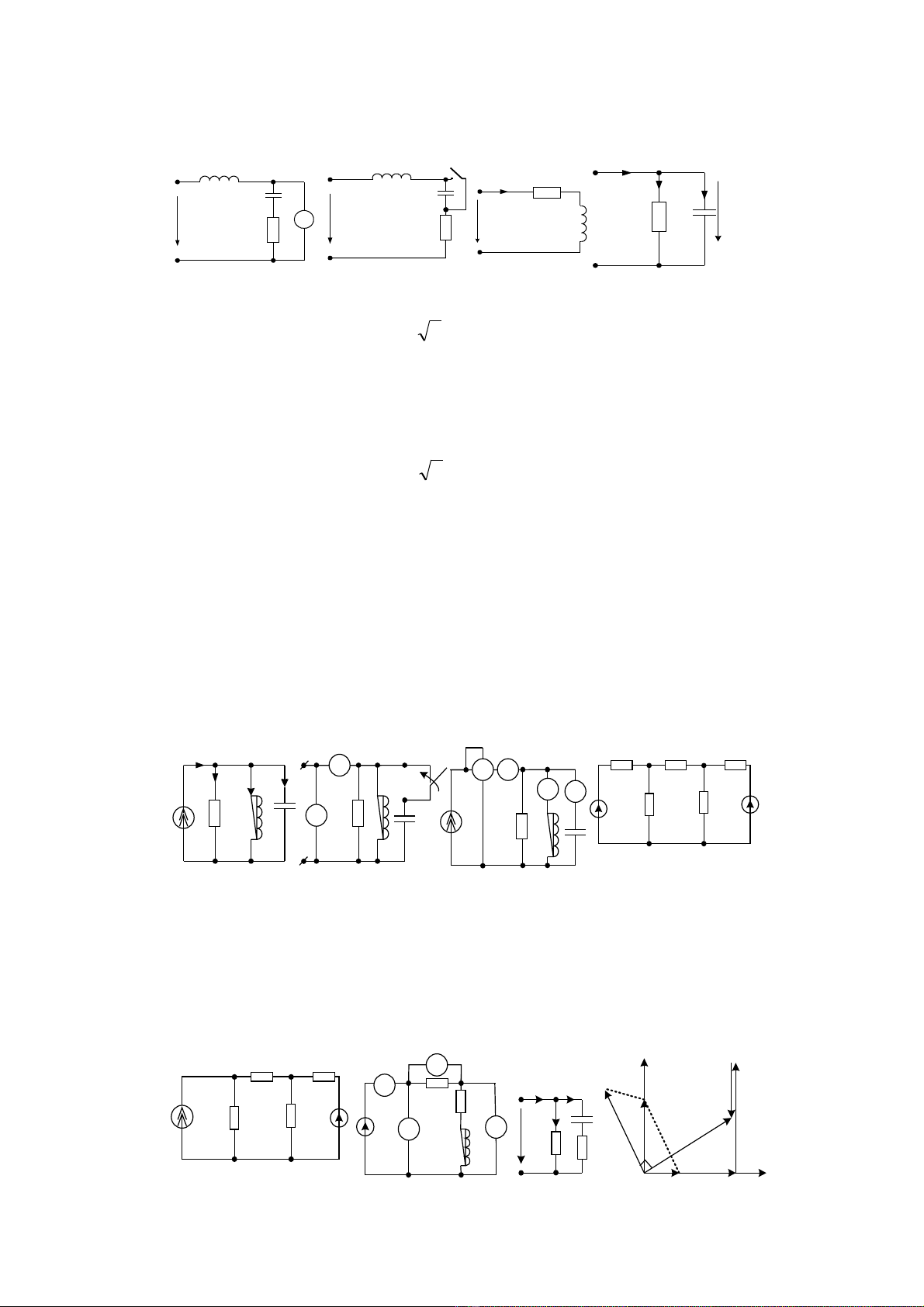
2.9. M ch đi n hình sin hình 2.7 bi t R=2ạ ệ ế Ω, L=20µH, C=2nF, đi n áp tác đ ng làệ ộ
u(t)=12cos(107t+120)[V]. Tính:
a) Các thông s c a m ch là t n s c ng h ng ố ủ ạ ầ ố ộ ưở ω0, tr kháng sóng ởρ, h s ph m ch t Q vàệ ố ẩ ấ
d i thông ả∆ω0,7.
b) Bi u th c t c th i c a dòng đi n và các đi n áp trên R, L, C.ể ứ ứ ờ ủ ệ ệ
c) Ch s c a các d ng c đo A, Vỉ ố ủ ụ ụ 1 và V2 và oat k W.ế
d) V đ th vect c a m ch.ẽ ồ ị ơ ủ ạ
2.10. M ch đi n hình sin hình 2.8 bi t R=20Kạ ệ ế Ω, L=2mH, C=0,2µF; dòng đi n tác đ ng làệ ộ
i(t)=10cos(107t+120)[mA]. Tính:
a) Các thông s c a m ch là t n s c ng h ng ố ủ ạ ầ ố ộ ưở ω0, tr kháng sóng ởρ, h s ph m ch t Q vàệ ố ẩ ấ
d i thông ả∆ω0,7.
b) Bi u th c t c th i c a đi n áp và các dòng đi n qua R, L, C. ể ứ ứ ờ ủ ệ ệ
c) V đ th vect c a m ch. ẽ ồ ị ơ ủ ạ
2.11. M ch đi n hình 2.9 có Xạ ệ L=6Ω; XC=3Ω; R=4Ω. Von k ch 100V. xác đ nh giá tr hi uế ỉ ị ị ệ
d ng c a đi n áp tác đ ng và góc l ch pha gi a đi n áp và dòng đi n trong m ch. ụ ủ ệ ộ ệ ữ ệ ệ ạ
2.12. M ch đi n hình 2.10 có R=6ạ ệ Ω; U=100V. Trong c hai tr ng h p đóng và h khoá Kả ườ ợ ở
ampe k đ u ch 10A. xác đ nh:ế ề ỉ ị
a) Các tr kháng XởL và XC.
H×nh 2.5
R
L
H×nh 2.7
C
V
V
A
1
2
H×nh 2.6
C
V
V
A
1
2
R L
R
W
V
1
V
2
u(t)
H×nh 2.8
u(t)
R L C
i(t)
A
43
b) Xây d ng đ th vect c a m ch trong c hai tr ng h p h và đóng khoá K. ự ồ ị ơ ủ ạ ả ườ ợ ở
2.13. Trong m ch đi n hình 2.11 công su t t c th i tính theo bi u th c:ạ ệ ấ ứ ờ ể ứ
]W[.t200cos55,2.t200cosSPu(t)i(t)p(t)
−=−==
Bi t đi n áp có bi u th c t c th i là u=ế ệ ể ứ ứ ờ
2
sin(100t+300). Tìm R và L.
2.14. M ch đi n hình 2.12 có dòng đi n iạ ệ ệ C(t)=10 cos(104t+300) [mA] và t ng d n ph c c aổ ẫ ứ ủ
m ch Y=0,01+j0,02ạ
a) Tìm bi u th c t c th i c a iể ứ ứ ờ ủ R(t), i(t) và u(t).
b) t n s nào thì dòng qua R và C có biên đ nh nhau.ở ầ ố ộ ư
2.15. Cho m ch đi n hình 1.13 bi t iạ ệ ế L=2
2
cos(5.103t), WM max=8.10-3Jun;
WE max=16.10-3Jun.
a) Xác đ nh các tham s R, L, C. ị ố
b) Tìm các dòng iR(t), iC(t), i(t).
2.16. Trong m ch đi n hình 1.14 khi đóng cũng nh h khoá K các d ng c đo đ u ch t ngạ ệ ư ở ụ ụ ề ỉ ươ
ng U=120V, I=10 A. Bi t R=15ứ ế Ω.
a) Xác đ nh XịL, XC.
b) Xây d ng đ th vect c a m ch trong c hai tr ng h p đóng và h khoá Kự ồ ị ơ ủ ạ ả ườ ợ ở
2. 17. Oát k trong m ch hình 1.15 ch 200W, Ampe k Aể ạ ỉ ế 1 ch 10 A, Ampe k Aỉ ế 2 ch 10 A,ỉ
Ampe k Aế3 ch 1,34 A. Tìm R, XỉL, XC. (ch d n:ỉ ẫ V đ th vect đ tính cho ti n).ẽ ồ ị ơ ể ệ
2.18. M ch đi n hình 2.16. bi t ạ ệ ế
,)22(
.
,)10
.
21 VjEVjE +==
Z1=(2+j2)Ω, Z2=(2-j2)Ω, Z3=(-
j2)Ω, Z4=j2Ω, Z5=j4Ω. Tính giá tr t c th i c a dòng qua nhánh Zị ứ ờ ủ 5.
2.19. Dùng d nh lý Theveneen-Norton tính đi n áp t c th i uị ệ ứ ờ ab(t) trong m ch hình 2.17. Bi t ạ ế
0
.
I
=1A, Z1=j Ω ; Z2=(1+j)Ω, Z3=(2-j)Ω, Z4=(1-j)Ω,
2
.
E
=(2j)V
u(t)
H×nh 2.9
L
C
H×nh 2.10
R
X
u(t)
V
X
H×nh 2.11
R
L
u(t)
C
K
u(t)
i(t)
R
L
H×nh 2.12
RC
i(t)
H×nh 2.13
R
C
i(t) LR
C
L
H×nh 2.14
A
V
RC
L
A
W
H×nh 2.15
A
A
1
23
Z
ZZ
ZZ
1 2
34
5
1
.
E
2
.
E
H×nh 2.16
K
H×nh 2.18
R
L
ZZ
ZZ
14
2
3
0
.
I
2
.
E
H×nh 2.17
VV
A
V
2
1
R
1
1
RR
C
u
H×nh 2.19
2
.
I
.
I
.
U
C
.
U
1
.
I
R
.
U
L
.
U
H×nh 2.20
a b II
I
1
2
44
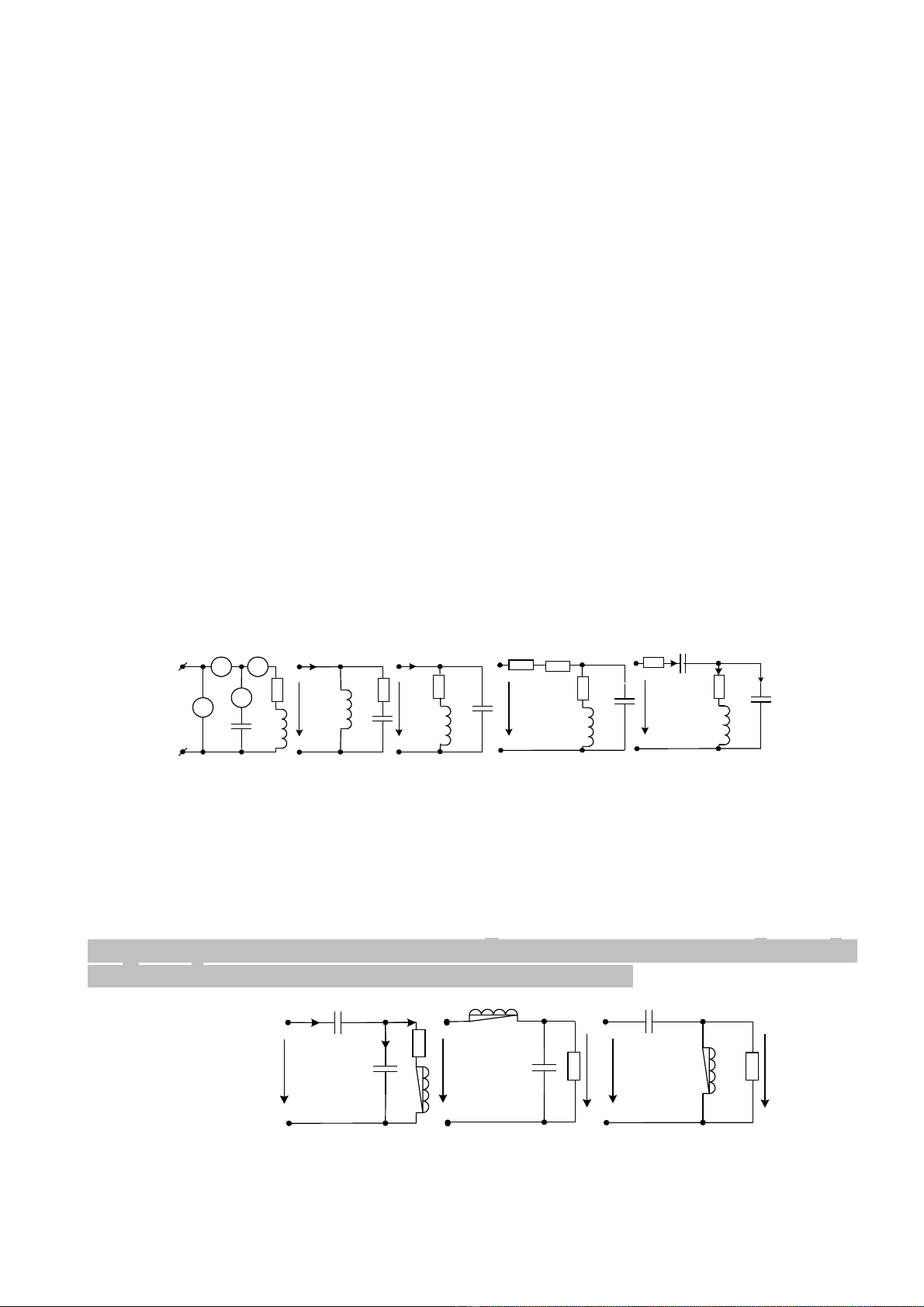
2.20. Các d ng c đo trên hình 2.18 ch nh sau: V ch 173V, Vụ ụ ỉ ư ỉ 1 ch 100V, Vỉ2 ch 100V, A chỉ ỉ
10A. Hãy xác đ nh:ị
a) R, R1, XL.
b) Công su t tiêu tán trên R. ấ
2.21. Trong m ch đi n hình 2.19 bi t Xạ ệ ế C=R và dòng đi n qua hai nhánh có cùng tr s hi uệ ị ố ệ
d ng. Hãy xây d ng đ th vect c a m ch, t đó xác đ nh góc l ch pha ụ ự ồ ị ơ ủ ạ ừ ị ệ ϕ gi a đi n áp vàữ ệ
dòng đi n trong m ch.ệ ạ
2.22. Hãy tìm m ch ng v i đ th vect trình bày trên hình 2.20. ạ ứ ớ ồ ị ơ
2.23. Các d ng c đo trên m ch hình 2.21 ch t ng ng U=200V, I=17,9 A, Iụ ụ ạ ỉ ươ ứ 1=I2=20A. Hãy
xác đ nh:ị
a) XC, R, XL
b) Công su t tiêu tán trong m ch. ấ ạ
2.24. Cho đo n m ch đi n hình 2.22 ch đ hình sin xác l p. Bi t R=10ạ ạ ệ ở ế ộ ậ ế Ω,
u(t)=40sin(300t-450) [V]
i(t)=3sin(300t-700) [A]
a) Tìm giá tr c a đi n dung C (ị ủ ệ tính b ng đ n v ằ ơ ị µF) và đi n c m L (ệ ả tính b ng đ n vằ ơ ị mH).
b) Tìm công su t tiêu tán trên đi n tr R.ấ ệ ở
2.25. Cho đo n m ch đi n hình 2.23 ch đ hình sin xác l p. ạ ạ ệ ở ế ộ ậ Bi t: R=8ếΩ,
u(t)=80 sin(500t-720) [V]
i(t)=3 sin(500t - 450) [A]
a) Tìm giá tr c a đi n dung C (ị ủ ệ tính b ng đ n v ằ ơ ị µF) và đi n c m L (ệ ả tính b ng đ n vằ ơ ị mH).
b) Tìm công su t tiêu tán trên đi n tr R.ấ ệ ở
2.26. Cho m ch đi n hình 2.24 bi t Rạ ệ ế 1=12,8Ω, R=4Ω, XL=4Ω, XC=6Ω.
a) Tìm tr s và tính ch t c a Xị ố ấ ủ 1 đ m ch đ t c ng h ng n i ti p.ể ạ ạ ộ ưở ố ế
b) Tìm công xu t tiêu tán trong m ch n u đi n áp tác đ ng có tr hi u d ng là 50V (khi c ngấ ạ ế ệ ộ ị ệ ụ ộ
h ng).ưở
2.27. Cho m ch đi n hình 2.25 bi t Rạ ệ ế 1=12,8Ω, XC1=2,4Ω; R=4Ω, XL=4Ω, XC2=6Ω. Công su tấ
tiêu tán trong m ch là P=2000W. Tìm tr s hi u d ng c a các dòng đi n trong m ch và c aạ ị ố ệ ụ ủ ệ ạ ủ
đi n áp tác đ ng.ệ ộ
2.28. M ch đi n hình 2.26 làm vi c t n s ạ ệ ệ ở ầ ố ω=105rad/s. Bi t UếC1=5V, C1=10µF, C2=5µF,
R=1Ω, L=20µH. Tìm tr s hi u d ng c a các đ i l ng U, I, Iị ố ệ ụ ủ ạ ượ 1, I2.
2.29. Cho m chạ
đi n hình 2.27ệ
a) Ch ng minhứ
r ng t n s c ngằ ầ ố ộ
h ng c a m ch cóưở ủ ạ
th đ c bi u di nể ượ ể ễ
b i công th c sau:ở ứ
H×nh 2.21
C
L
R
C
L
H×nh 2.22
A
R
2
VA
A
1
u(t)
i(t)
X
X
H×nh 2.24
R
u
XR
11
L
C
C
L
H×nh 2.25
R
U
C
2
1
II
I
2
1
C
H×nh 2.23
R
u(t)
i(t)
L
R
1
H×nh 2.28
L
R
C
1
.
U
2
.
U
L
H×nh 2.27
R
C
1
.
U
2
.
U
CR
C
.
U
H×nh 2.26
1
2
L
II
I
2
1
45