PHỤ LỤC A: TÍNH TOÁN HỆ SỐ HỒI QUY
Cao Văn Trường _ QG10_1051170069 Trang 1
PHỤ LỤC A: TÍNH TOÁN HỆ SỐ HỒI QUY
Mô hình phát sinh (P) và thu hút (A) chuyến đi được xây dựng là các hàm
hồi quy tuyến tính 3 biến với các biến là số lượng dân số, số lượng lao động và số
lượng học sinh sinh viên. Cụ thể kết quả tính toán như sau:
Mô hình phát sinh chuyến đi:
Pi = ai*Population + bi*Workers + ci*Students
Mô hình thu hút chuyến đi:
Aj = xj*Population + yj*Workers + zj*Students
Trong đó: Population : Dân số
Workers : Số lao động
Students : Số HSSV
ai, bi, ci, xj, yj, zj là tham số, hệ số hồi quy tương ứng.
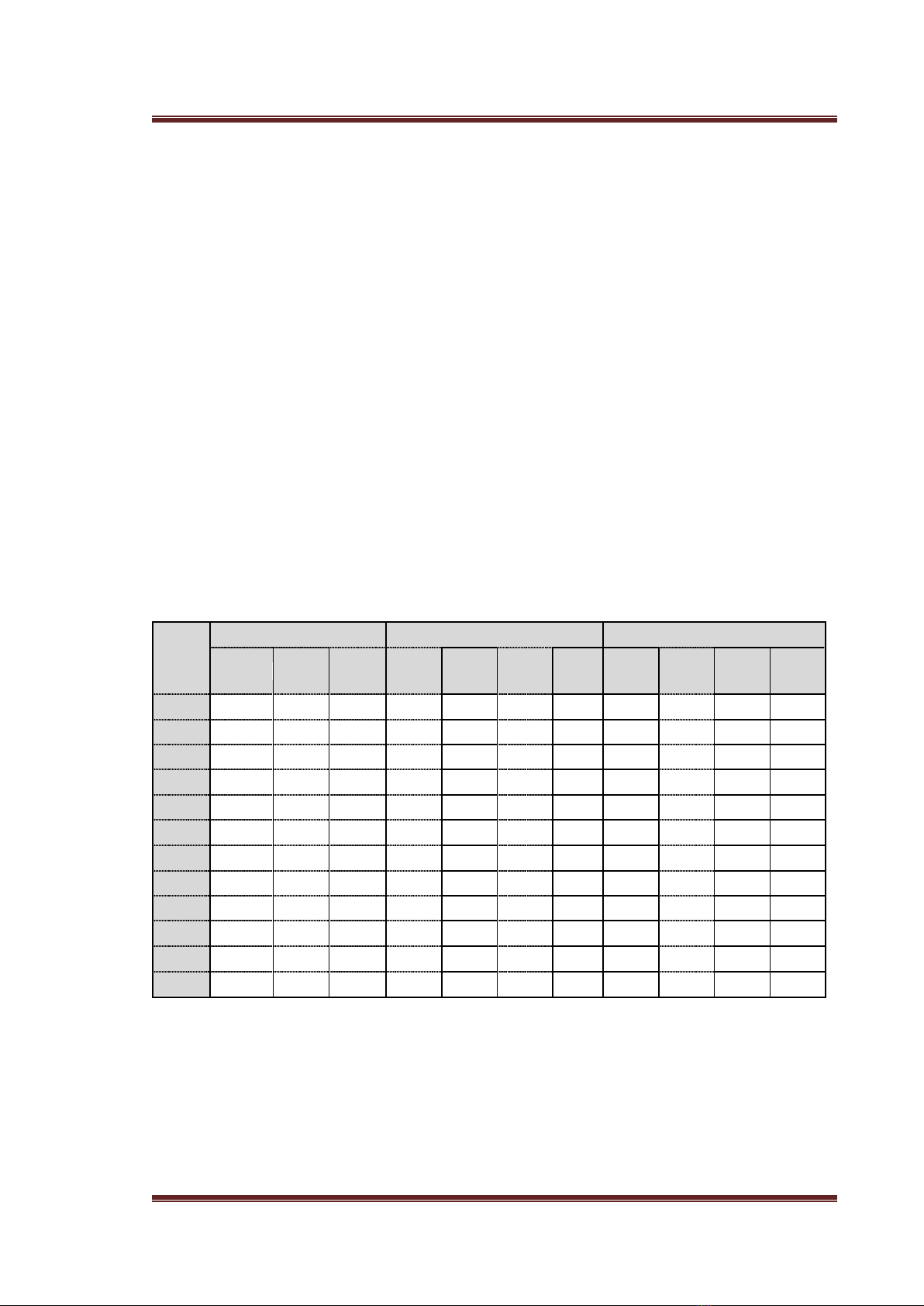
Các dự liệu đầu vào sử dụng hàm hồi quy được trình bày trong Bảng 1.
Bảng 1. Dữ liệu đầu vào hàm hồi quy
Zone
Các biến số
Phát sinh chuyến đi năm 2014
Thu hút chuyến đi năm 2014
Dân số
Lao
động
HSSV
HBW
HBO
NHB
HBS
HBO
NHB
1
15427
3350
4203
1190
5269
623
4203
1190
1020
2
24207
3910
1755
653
4518
1198
1755
653
1905
3
21868
3792
5952
1224
2448
233
5952
1224
2507
4
15691
4465
4898
2418
1582
220
4898
2418
1846
5
10144
2718
1487
635
2365
388
1487
635
494
6
15577
4646
4750
2575
3829
660
4750
2575
1848
7
17903
3100
4305
1786
1939
306
4305
1786
2449
8
20776
3056
6295
916
3148
1259
6295
916
4063
9
36178
7830
9775
4245
5488
569
9775
4245
3313
10
20072
5613
7168
2434
2816
382
7168
2434
2339
11
16157
3415
1887
980
4214
539
1887
980
1519
Tổng
214000
45895
52475
19056
37616
6378
52475
19056
23304
Với các dữ liệu trên sử dụng công cụ Microsofl Excel để tính toán hồi quy
cho từng giá trị của từng chuyến đi phát sinh(P) và thu hút (A).
Kết quả tính toán của hàm hồi quy cho chuyến đi Phát sinh với mục đích
HBW như sau:
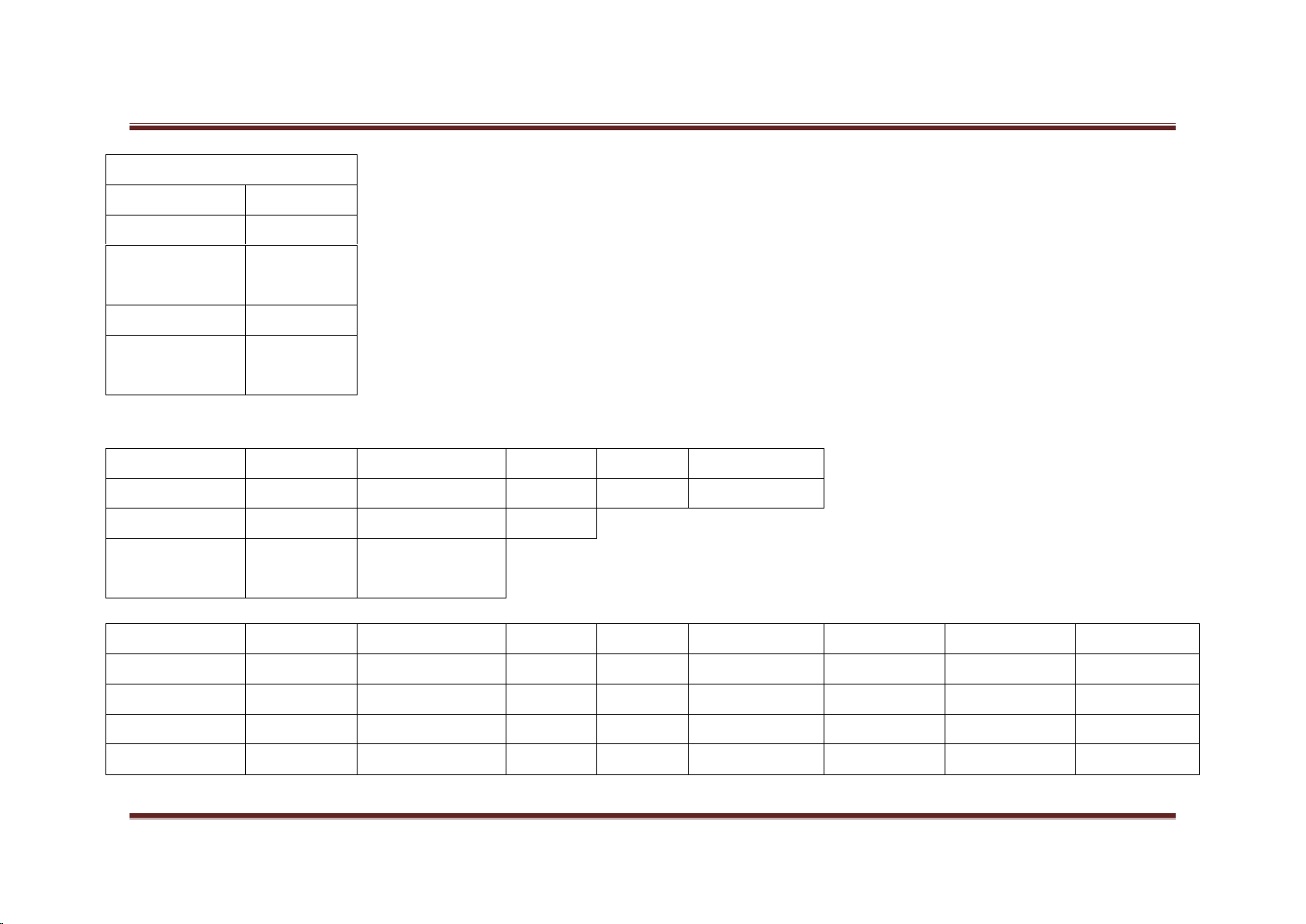
Bảng 2: Kết quả hồi quy Phát sinh chuyến đi với mục đích HBW trong Excel
PHỤ LỤC A: TÍNH TOÁN HỆ SỐ HỒI QUY
Cao Văn Trường _ QG10_1051170069 Trang 2
Regression Statistics
Multiple R (R)
0.979238
R Square (R2)
0.958907
Adjusted R
Square
0.823634
Standard Error
481.5898
Observations
( Số mẫu n)
11
ANOVA
df
SS
MS
F
Significance F
Regression
(k) 3
ESS 43296957
14432319
62.22738
2.06E-05
Residual
(n-k) 8
RSS 1855430
231928.7
Total
11
TSS=ESS+RSS
45152387
Coefficients
Standard Error
t Stat
P-value
Lower 95%
Upper 95%
Lower 95.0%
Upper 95.0%
Intercept
0
#N/A
#N/A
#N/A
#N/A
#N/A
#N/A
#N/A
Dân số
-0.07706
0.033757
-2.2829
0.051836
-0.15490576
0.00078001
-0.154905764
0.00078
Lao động
0.595462
0.173266
3.436699
0.008867
0.19591068
0.995013946
0.195910683
0.995014
HSSV
0.169772
0.09496
1.787828
0.111609
-0.04920606
0.388750652
-0.049206065
0.388751
PHỤ LỤC A: TÍNH TOÁN HỆ SỐ HỒI QUY
Cao Văn Trường _ QG10_1051170069 Trang 3
Bảng tóm tắt kết quả tính toán SUMMARY OUTPUT:
Hàm hồi quy có dạng Pi = ai*Populationi + bi*Workersi + ci*Studentsi
Regression Statistics: Các thông số của mô hình hồi quy
Multiple R: Hệ số tương quan bội (0<=R<=1). R= 0.979238 cho thấy mức
độ chặt chẽ của mối liên hệ tương quan bội.
R Square: Hệ số xác định. Với R2=
=
=0.958907 trong 100%
sự biến động của biến phụ thuộc P (số chuyến đi phát sinh với mục đích HBW) thì
có 95,89 % sự biến động là do các biến độc lập Population, Workers, Students ảnh
hưởng, còn lại là do sai số ngẫu nhiên.
Adjusted R: Hệ số xác định mẫu điều chỉnh. Là hệ số xác định có tính đến
độ lớn hay nhỏ của bậc tự do df. Cho thấy mức ảnh hưởng của việc tăng thêm biến
số.
Standard Error: Sai số chuẩn của P do hồi quy là 910.
Observation: Số quan sát hay dung lượng mẫu là 11. Đây chính là số Zone
nội vùng.
Bảng phân tích phương sai ANOVA (Analysis of variance):
Regression: Do hồi quy. Số lượng các biến độc lập k =3 ( Population,
Workers, Students)
Residual: Do ngẫu nhiên. Giá trị này được xác định bằng hiệu số mẫu quan
sát n và số biến độc lập k. Vậy n-k = 11-3 = 8.
Total: Tổng của Regression và Residual = 3+8 = 11.
Df (Degree of freedom): Số bậc tự do.
SS (Sum of Square): Tổng bình phương của mức động (sai lệch) giữa các
giá trị quan sát của Y (ký hiệu là Y
i
) và giá trị bình quân của chúng.
MS (Mean of Square): Phương sai hay số bình quân của tổng bình phương
sai lệch kể trên
TSS ( Total Sum of Square)= ESS+TSS= 45152387 là Tổng bình phương
của tất cả các mức sai lệch giữa các giá trị quan sát P
i
và giá trị bình quân của
chúng
PHỤ LỤC A: TÍNH TOÁN HỆ SỐ HỒI QUY
Cao Văn Trường _ QG10_1051170069 Trang 4
Do hồi quy Regression ESS (Explained Sum of Square)= 43296957 là
tổng bình phương các sai lệch giữa các giá trị của biến phụ thuộc P (số chuyến đi
phát sinh với mục đích HBW) nhận được từ hàm hồi quy mẫu (ký hiệu P*
i
). Độ
lớn của ESS phản ánh mức độ giao động của các giá trị cá biệt của mô hình với
giá trị trung bình mẫu hàm hồi quy.
ESS=Σi (P * i P 2
Do ngẫu nhiên Residual RSS (Residual Sum of Square) là tổng bình
phương của tất cả các sai lệch giữa các giá trị quan sát của P (P
i
) và các giá trị
nhận được từ hàm hồi quy P*i
RSS ie2 i
P -P * i2 1855430
Ta có thể kiểm tra chéo như sau:
TSS = ESS + RSS = 45152387
R
2
= ESS/ TSS= 0.958907
F-stat: Tiêu chuẩn F dùng làm căn cứ để kiểm định độ tin cậy về mặt
khoa học (thống kê) của toàn bộ phương trình hồi quy.
Significance F: F lý thuyết.
Bảng phân tích hồi quy:
- Coefficients: Cột giá trị của các hệ số hàm hồi quy: β1 = -0.07706,
β2 = 0.595462, β3 = 0.169772 với β1, β2 , β3 : là các hệ số ước lượng, các hệ số hồi
quy này phản ánh mức độ ảnh hưởng của từng biến độc lập ( Dân số, Lao động,
HSSV) đến biến phụ thuốc P1 (số chuyến đi phát sinh với mục đích HBW).
Trong quá trình phỏng vấn khảo sát thực tế, số chuyến đi khảo sát không
nhiều và kết quả khảo sát phải qua 1 bước hiệu chỉnh nên kết quả hồi quy này xuất
hiện sai số và các giá trị mang dấu (-) nhưng các sai số này có thể chấp nhận được.
- Intercept: Hệ số tự do. Hệ số này cho thấy xuất phát điểm của đường hồi
quy. Tuy nhiên ở đây ta không xét đến hệ số tự do này.
Standard Error: (se) độ lệch chuẩn của mẫu theo biến
t-stat: Tiêu chuẩn t dùng làm căn cứ để kiểm định độ tin cậy về mặt khoa học
PHỤ LỤC A: TÍNH TOÁN HỆ SỐ HỒI QUY
Cao Văn Trường _ QG10_1051170069 Trang 5
(thống kê) của độ co giãn a
i
( a1= -2.2829, a2= 3.436699 , a3= 1.787828) tức là
của mối liên hệ giữa các biến số độc lập ( Dân số, Lao động, HSSV) và hàm phụ
thuộc P (số chuyến đi phát sinh với mục đích HBW).
P-value: Xác suất để t > t-stat, dùng kiểm định độ tin tin cậy về mặt khoa học
(thống kê) của độ co giãn a
i
tức là của mối liên hệ giữa các biến số độc lập ( Dân
số, Lao động, HSSV) và hàm phụ thuộc P (số chuyến đi phát sinh với mục đích
HBW).
Lower 95%, Upper 95%, Lower 98%, Upper 98%: là cận dưới và cận trên
của khoảng ước lượng cho các tham số với độ tin cậy 95% và độ tin cậy 98%.
Nhận xét: Dựa vào bảng kết quả trên ta có phương trình hồi quy cho chuyến
đi Phát sinh với mục đích HBW như sau:
P1 = -0.07706*Dân số + 0.595462*Lao động + 0.169772*HSSV
Như vậy với dữ liệu dự báo năm 2020 của Zone 1 là: Dân số = 15859, Lao
động = 3444, HSSV = 4321 thì giá trị dự báo của P1 được tính như sau:
P1 = -0.07706*15859 + 0.595462*3444 + 0.169772*4321= 1562 (chuyến
đi/ngày)
Tức là số chuyến đi phát sinh với mục đích HBW của Zone 1 năm dự báo
2020 sẽ là 1520 chuyến đi/ngày.
Ngoài ra, dựa vào bảng kết quả hồi quy ( Bảng 2) ta cũng thấy:
Nếu Số lao động và Số HSSV không đổi thì cứ tăng Dân số 1 người sẽ làm
cho Số chuyến đi Phát sinh với mục đích HBW giảm đi 0.07706 chuyến đi. Điều
này trái với thực thế. Trong trường hợp này số chuyến đi khảo sát được không nhiều
và số lượng mẫu thống kê n nhỏ nên sai số có thể chấp nhận được.
Nếu Dân số và Số HSSV không đổi thì cứ tăng Số Lao động lên 1 người sẽ
làm cho Số chuyến đi Phát sinh với mục đích HBW tăng lên 0.595462 chuyến đi.
Điều này chứng tỏ mức độ ảnh hưởng của Số Lao động lên Số chuyến đi Phát sinh
với mục đích HBW là rất lớn.
Nếu Dân số và Số lao động không đổi thì cứ tăng Số HSSV lên 1 người sẽ
làm cho Số chuyến đi Phát sinh với mục đích HBW tăng lên 0.169772 chuyến đi.