Tổ Toán - Trường THPT Bình Điền
Tổ Toán Trường THPT Bình Điền. 1
Tiết 28: PHƯƠNG TRÌNH TỔNG QUÁT CỦA ĐƯỜNG THẲNG.
I. Mục tiêu:
Qua bài học này học sinh cần nắm được:
1. Về kiến thức:
Vận dụng phương trình tổng quát của đường thẳng để lập phương trình tổng quát của các đường
thẳng.
2. Về kỹ năng:
Lập được phương trình tổng quát của đường thẳng, xát định được vị trí tương đối giữa hai đường
thẳng.
3. Về tư duy:
Biết quy lạ về quen.
4. Về thái độ:
Cẩn thận, chính xác.
II. Phương tiện:
1. Thực tiển:
Học sinh đã học bài hàm số bậc nhất ở lớp 9.
2. Phương tiện:
Bảng phụ, bảng kết quả.
III. Gợi ý về phương pháp:
Cơ bản dùng phương pháp vấn đáp gợi mở thông qua hoạt động điều khiển tư duy thông qua hoạt
động nhóm.
IV. Quá trình dạy học:
1. Kiểm tra bài cũ:
Trong mặt phẳng tạo độ Oxy cho A(a;0); B(0;b) (a.b
≠
0).
Chứng minh rằng đường thẳng đi qua hai điểm AB có dạng:
a
x+b
y= 1.
Hs:
A
B=(-a;b).
Véctơ pháp tuyến của đường thẳng AB là: n=(-b;-a).
Phương trình tổng quát của đường thẳng AB:
-b(x-a)-a(y-0) = 0.
⇔ -bx-ay = -ab
⇔ a
x+b
y= 1
Phương trình đường thẳng trên gọi là phương trình đoạn chắn.
2. Bài mới:
Hoạt động của Giáo viên Hoạt động của Học sinh Nội dung ghi bảng
Hoạt động 1:
Đường thẳng: ax + by + c = 0 (d)
Khi b 0 thì y bằng gì?
≠
y = - b
ax - b
c
y = kx + m ( k = - b
a; m = - b
c)
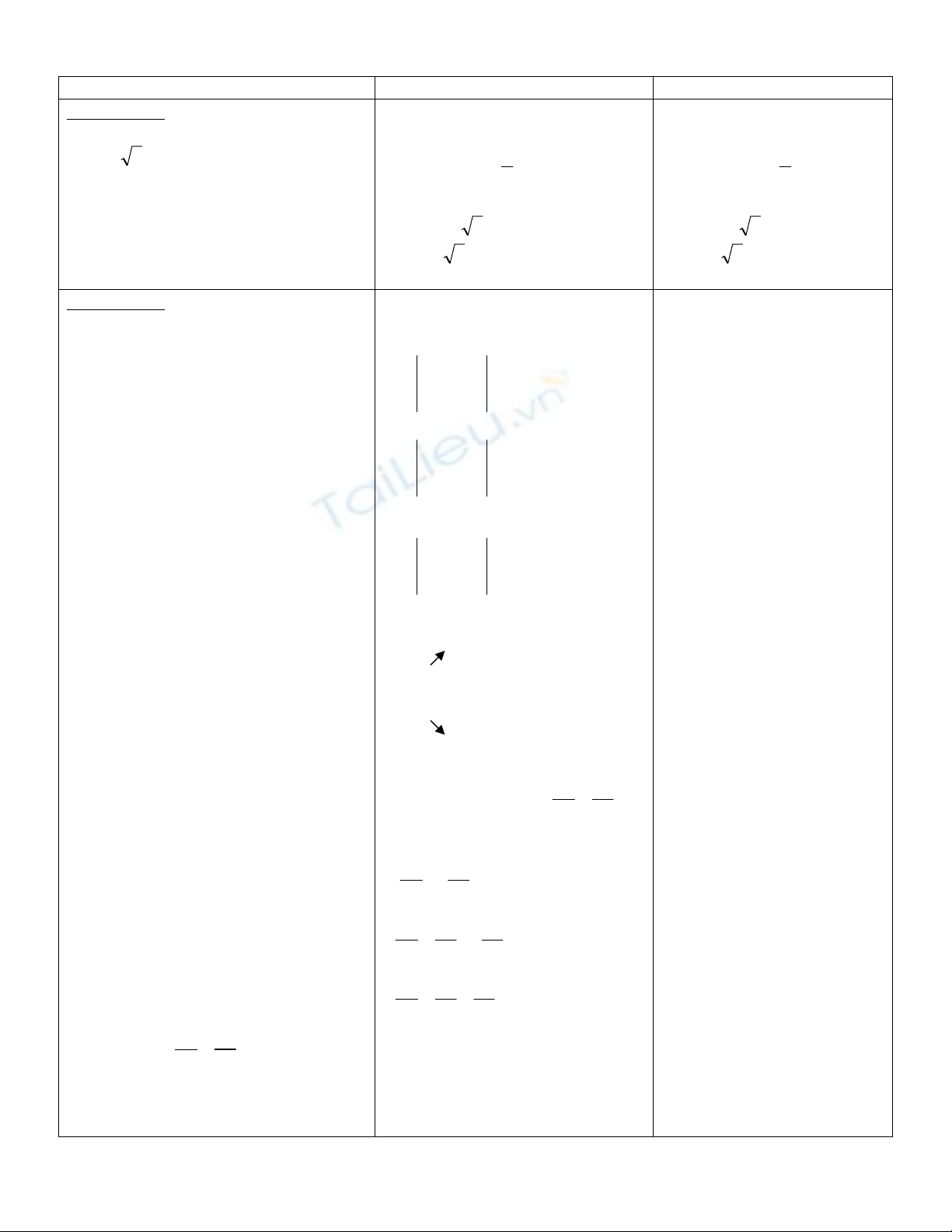
y
k = tan
α
α
Phương trình đường thẳng
theo hệ số góc là:
y = kx + m (d).
Tổ Toán - Trường THPT Bình Điền
Tổ Toán Trường THPT Bình Điền. 2
O x
Hoạt động 2:
(Δ1) : 2x + 2y – 1 = 0.
(Δ2) : 3 x – y + 5 = 0.
Chỉ ra hệ số góc và góc tương ứng giữa
hai đường thẳng trên.
GV: Cho học sinh thảo luận và trả lời.
Hs:
(
Δ
1) : y = -x + 2
1
→ k = -1;
α
1= 135o
(
Δ
2) : y = 3 x + 5
→ k = 3;
α
2= 60o
(Δ1) : y = -x + 2
1
→ k = -1;
α
1= 135o
(Δ2) : y = 3 x + 5
→ k = 3;
α
2= 60o
Hoạt động 3:
(Δ1) : a1x + b1y + c1 = 0
(Δ2) : a2x + b2y + c2 = 0
Gv: Hai đường thẳng ( Δ1), (
Δ
2) cắt
nhau, song song, trùng nhau khi nào?
Gv: Khi D = 0 ta có tỉ lệ thức nào?
?1. Tỉ lệ thức a
a
2
1=b
b
2
1 có thể nói gì về
vị trí tương đối của ( Δ1) và ( Δ2)?
Hs: Hoạt động theo nhóm rồi trả
lời:
D = = a
ba ba
22
11 1b2 – a2b1
Dx= = c
bc bc
22
11 1b2 – c2b1
Dy= = a
ca ca
22
11 1c2 – a2c1
D
≠
0 (
→
Δ
1) cắt (
Δ
2) .
Dx
≠
0 hay Dx
≠
0 :
(
Δ
1) // (
Δ
2)
D = 0
Dx = Dy = 0:
(
Δ
1)
≡
(
Δ
2)
Hs: a1b2 – a2b1 = 0 →a
a
2
1=b
b
2
1
Do đó ta có:
* a
a
2
1
≠
b
b
2
1
⇔
(
Δ
1) cắt (
Δ
2)
*a
a
2
1=b
b
2
1
≠
c
c
2
1
⇔
(
Δ
1) // (
Δ
2)
*a
a
2
1=b
b
2
1=c
c
2
1
⇔
(
Δ
1)
≡
(
Δ
2)
Hs: song song hay trùng.
* (SGK)
Tổ Toán - Trường THPT Bình Điền
Tổ Toán Trường THPT Bình Điền. 3
Hoạt động 4:
Xét vị trí tương đối giữa các cặp đường
thẳng sau?
a) (Δ1) 2x – 3y + 5 và
( Δ2) x + 3y - 3 = 0
b) (Δ1) x – 3y + 2 = 0 và
( Δ2) -2x + 6y + 3 = 0
c) (Δ1) 0,7x + 12y – 5 = 0 và
( Δ2) 1,4x + 24y – 10 = 0
GV: Cho học sinh thảo luận và trả lời.
a) Do 1
2
≠
3
3
−
nên (
Δ
1) cắt (
Δ
2)
b) Do 2
1
− = 6
3
−
≠
3
2
nên (
Δ
1) // (
Δ
2)
c) Do 4,1
7,0 = 24
12 = 10
5
−
−
nên (
Δ
1)
≡
(
Δ
2)
a) Do 1
2
≠
3
3
−
nên ( Δ1) cắt (
Δ
2)
b) Do 2
1
− = 6
3
−
≠
3
2
nên ( Δ1) // ( Δ2)
c) Do 4,1
7,0 = 24
12 = 10
5
−
−
nên ( Δ1) ≡ ( Δ2)
Hoạt động 5:
Cho N(-2;9) và đường thẳng
(d) : 2x – 3y + 18 = 0.
a) Tìm tọa độ hình chiếu H của N
lên (d).
b) Tìm tọa độ điểm đối xứng của
N qua (d).
Gv: Cho học sinh đọc đề và vẽ hính:
GV: Cho học sinh làm bài theo nhóm.
Hs:
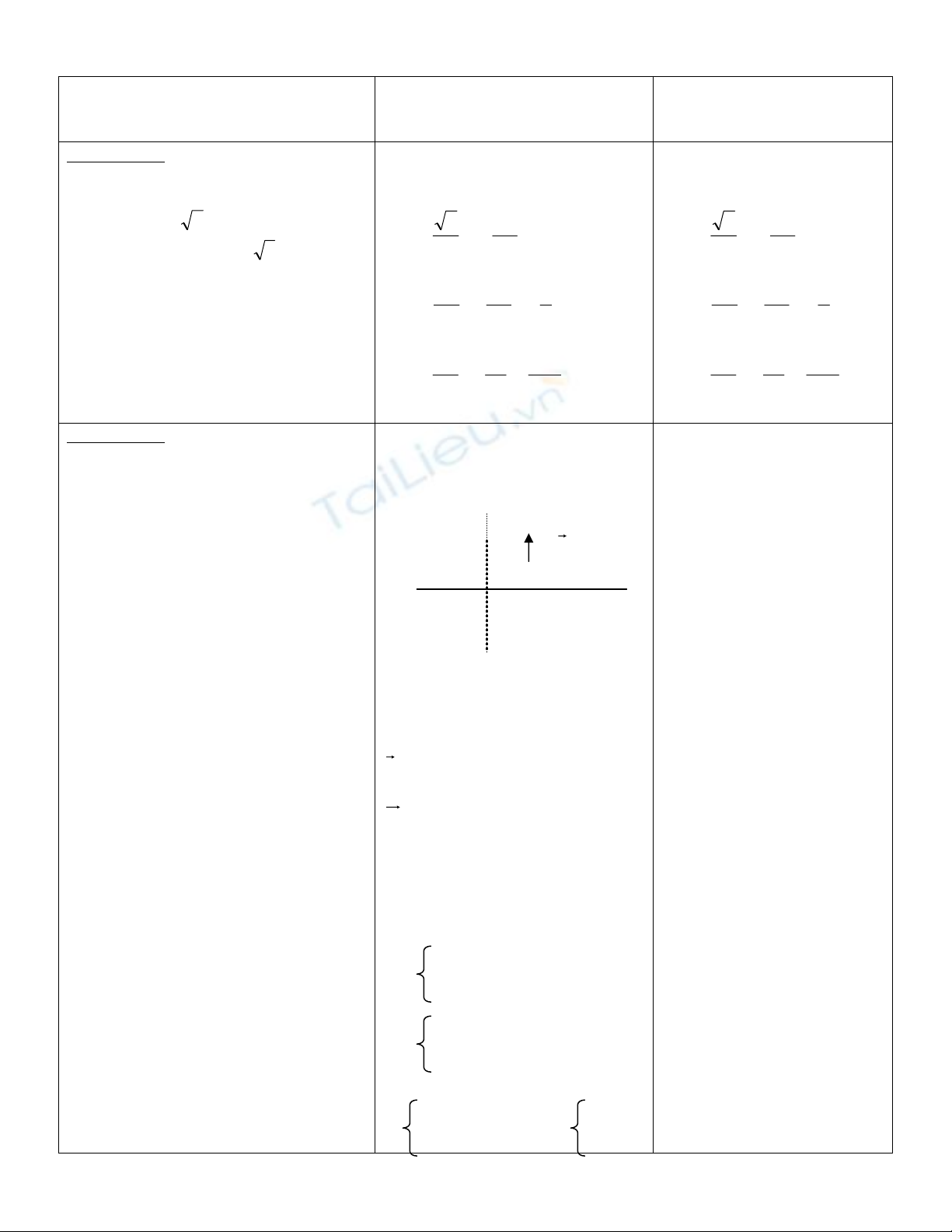
(
Δ
)
N u
(d)
H
N’
Hs:
- Viết đường thẳng (
Δ
) qua N và
⊥
với (d).
Véctơ pháp tuyến của (d) :
n= (2;-3)
Véctơ pháp tuyến của (
Δ
) :
'
n= (3; 2)
Phương trình đường thẳng (
Δ
):
3(x + 2) + 2(y – 9) = 0
⇔
3x + 2y – 12 = 0
- Tọa độ điểm H là nghiệm của hệ:
2x – 3y + 18 = 0
3x + 2y – 12 = 0
x = 0
⇔
y = 6
Như vậy H (0;6)
xN + xN’ = 2xH xN’ = 2
-
⇔
H (0;6)

Tổ Toán - Trường THPT Bình Điền
Tổ Toán Trường THPT Bình Điền. 4
yN + yN’ = 2yH yN’ = 3
Vậy N’(2;3).
N’(2;3).


























