Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
523
ỨNG DỤNG MÔ HÌNH HỌC MÁY LINEAR REGRESSION (LR)
VÀ RANDOM FOREST (RF) VÀ K-NEAREST NEIGHBORS (KNN)
TRONG DỰ BÁO MỰC NƯỚC HỆ THỐNG SÔNG HẬU -
ĐỒNG BẰNG SÔNG CỬU LONG
Trần Đăng An1, Thái Hữu Hùng1, Trần Xuân Thủy2, Triệu Ánh Ngọc1
1Trường Đại học Thủy lợi, email: ngocta@tlu.edu.vn
2Viện Công nghệ Tài nguyên nước và Môi trường
1. GIỚI THIỆU CHUNG
Dự báo mực nước là yếu tố quan trọng trong
quản lý tài nguyên nước, phòng chống thiên tai
và quy hoạch đô thị. Các phương pháp truyền
thống như mô hình toán học, thủy văn và thủy
lực gặp nhiều hạn chế do yêu cầu dữ liệu chi
tiết và độ phức tạp cao [1] [2] [3]. Trong bối
cảnh đó, các mô hình học máy (Machine
Learning) đã được phát triển và ứng dụng như
công cụ hữu ích trong việc xử lý lượng dữ liệu
lớn và học từ các mẫu dữ liệu lịch sử để dự báo
chính xác các thông số khí tượng thủy văn và
môi trường. Trong đó, phương pháp hồi quy
tuyến tính (Linear Regression - LR) được xem
là hiệu quả nhờ sự đơn giản và khả năng áp
dụng rộng rãi [4]. Nhiều nghiên cứu đã khẳng
định hiệu quả của Machine Learning trong dự
báo mực nước. Mosavi et al. (2018) đã áp dụng
Machine Learning để dự báo mực nước lũ và
đạt độ chính xác cao hơn so với các phương
pháp truyền thống với chỉ số xác định R2 >
0,85 và hệ số sai số < 0,2 [5].
Trong nghiên cứu này, ba phương pháp: K-
Nearest Neighbors (KNN), Linear Regression
(LR) và Random Forest Regression (RFR),
được sử dụng để phân tích độ tin cậy, tính
chính xác của từng phương pháp. Trạm thủy
văn Cần Thơ (trên sông Hậu) được sử dụng
để dự báo mực nước trong vòng 6 tháng để
làm rõ ưu điểm và hạn chế của các phương
pháp, khẳng định tính khả thi và hiệu quả
của Machine Learning trong quản lý tài
nguyên nước.
2. PHƯƠNG PHÁP NGHIÊN CỨU
Nhóm nghiên cứu sử dụng ba phương
pháp: (a) K-Nearest Neighbors (KNN), (b)
Linear Regression (LR), (c) Random Forest
Regression.
Hình 1. Phương pháp hồi quy KNN (a),
LR (b) và RFR (c)
(a) K-Nearest Neighbors (KNN) - Phương
pháp này dự đoán giá trị của một mới bằng
cách dựa vào thông tin từ K điểm dữ liệu gần
nhất trong tập huấn luyện (K-lân cận).
(b) Linear Regression (LR) - Phương pháp
này tìm một đường thẳng (hoặc siêu phẳng
trong trường hợp đa biến) phù hợp nhất với
dữ liệu, nhằm dự đoán giá trị của biến phụ
thuộc dựa trên giá trị của biến độc lập.
(c) Random Forest Regression (RFR) -
Phương pháp này tổng hợp kết quả từ nhiều
cây quyết định đơn lẻ, từ đó nâng cao hiệu
quả dự báo thông qua hình thức biểu quyết đa
số hoặc tính trung bình kết quả, tùy theo từng
bài toán cụ thể.
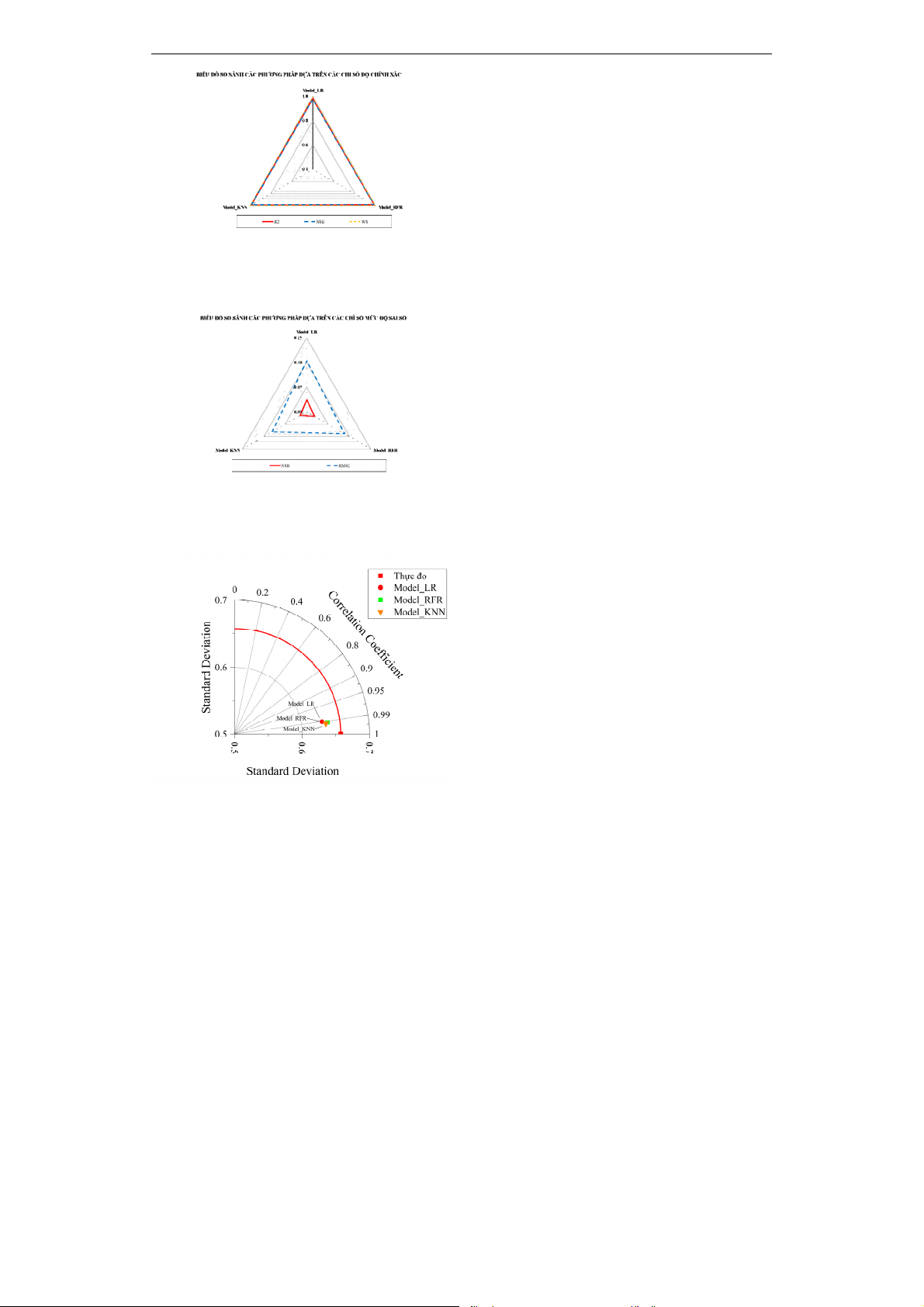
Để đánh giá mức độ dự báo chính xác của
các mô hình hồi quy, các tiêu chí đánh giá
sau đây được sử dụng: hệ số sai số - NSR (1),
RMSE (2). Và hệ số độ chính xác - R2 (3),
NSE (4) và WS (5). Công thức được thể hiện
dưới đây:
Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
524
2
2
(
)
)
(

ii
i
CaObs
SSE
NSR SST Ob Obss
l (1)
2
1()
ii
RMSE Obs Cal
n (2)
2
1
2
22
11
(
(
).( )
). )(






n
ii
i
nn
ii
ii
Obs
Obs Ca
Obs Cal Cal
R
Obs Call
(3)


2
2
1

ii
i
Obs Cal
O
N
Obs bs
SE (4)


2
1
2
1
1


N
ii
i
N
ii
i
Obs Cal
WS
Cal O bsbsObs O
(5)
trong đó: Obs là giá trị thực đo, Cal là giá trị
tính toán.
Sông Hậu chịu tác động lớn từ các dòng
chảy phụ lưu đổ vào, do đó việc dự báo mực
nước tại trạm thủy văn Cần Thơ cần xem xét
các yếu tố này nhằm nâng cao hiệu quả của
mô hình dự báo.
Hình 2. Hệ thống sông tại Đồng bằng
sông Cửu Long và các trạm khí tượng,
thủy văn trong khu vực
Trạm Cần Thơ nằm giữa đoạn sông Hậu
(Đồng bằng sông Cửu Long) và biển, chịu tác
động rất lớn của triều Biển Đông và lưu lượng
thượng nguồn. Nhằm nâng cao độ chính xác
và tin cậy trong tính toán, hai trạm thủy văn
thượng nguồn (Châu Đốc và Long Xuyên)
được đưa vào mô hình như hai biến độc lập
trong huấn luyện dự báo mực nước tại trạm
Cần Thơ.
3. KẾT QUẢ NGHIÊN CỨU
Chuỗi dữ liệu mực nước theo giờ thu thập
10 năm từ 01/01/2013 đến 31/12/2022 cho 3
trạm (Tân Châu, Long Xuyên và Cần Thơ)
được sử dụng trong nghiên cứu này. Trong
đó, chuỗi dữ liệu 01/01/2013 đến 31/12/2021
(9 năm) tại Châu Đốc và Long Xuyên được
sử dụng để huấn luyện các mô hình học máy
(Machine Learning), và mực nước từ
01/01/2022 đến 31/06/2022 tại Trạm Cần
Thơ để kiểm định và đánh giá độ tin cậy của
các mô hình dự báo trong thời đoạn này. Kết
quả được thể hiện tại hình 3, 4, 5, 6, 7, 8.
Hình 3. Đường quá trình mực nước giữa
kết quả dự báo bằng phương pháp LR
và thực đo tại trạm Cần Thơ
Hình 4. Đường quá trình mực nước giữa
kết quả dự báo bằng phương pháp RFR
và thực đo tại trạm Cần Thơ
Hình 5. Đường quá trình mực nước giữa
kết quả dự báo bằng phương pháp KNN
và thực đo tại trạm Cần Thơ
Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
525
Hình 6. Biểu đồ so sánh độ chính xác
của mô hình giữa các chỉ số
Hình 7. Biểu đồ so sánh mức độ sai số
của mô hình giữa các chỉ số
Hình 8. Biểu đồ Taylor thể hiện độ chính xác
của mô hình với giá trị thực đo
Kết quả cho thấy, cả ba phương pháp đều
có độ tin cậy và chính xác cao trong dự báo
mực nước với R² = 0,988, NSE = 0,985
(KNN), với R² = 0,984, NSE = 0,982 (RFR)
và R² = 0,98, NSE = 0,975 (LR). Hơn nữa,
kết quả đạt được chỉ ra rằng mô hình KNN có
độ độ chính xác tốt nhất qua các chỉ số R²,
NSE, đồng thời đạt được các hệ số sai số là
nhỏ nhất (RMSE = 0,08, NSR = 0.015). Khả
năng mô phỏng mối quan hệ phi tuyến tính
trong dữ liệu giúp KNN dự báo chính xác
hơn. RFR cũng đạt kết quả tốt nhờ việc kết
hợp nhiều cây quyết định. LR, dựa trên tính
toán mối quan hệ tuyến tính giữa các biến
độc lập và biến phụ thuộc, tuy đơn giản
nhưng vẫn đạt hiệu suất tốt.
4. KẾT LUẬN
Trong nghiên cứu này, ba mô hình dự
đoán mực nước theo giờ tại trạm Cần Thơ
trên sông Hậu đã được xây dựng dựa trên các
phương pháp hồi quy LR, RFR và KNN. Bộ
dữ liệu từ hai trạm Châu Đốc và Long Xuyên
được sử dụng để huấn luyện và kiểm định các
mô hình. Kết quả cho thấy mô hình KNN có
khả năng dự báo chính xác nhất, thể hiện qua
các chỉ số thống kê R², NSE, và RMSE. Điều
này khẳng định độ tin cậy và tính chính xác
của KNN. Mặc dù hiệu quả mô hình phụ
thuộc vào việc xác định chính xác điểm khởi
nguồn, nhưng phương pháp máy học đã minh
chứng là (1) công cụ hiệu quả để theo dõi và
dự báo biến động mực nước, (2) đơn giản
hơn so với các mô hình toán truyền thống mà
vẫn đảm bảo độ chính xác cao.
5. TÀI LIỆU THAM KHẢO
[1] Beven, K. (2012). Rainfall-Runoff
Modelling: The Primer. John Wiley & Sons.
[2] Wheater, H., & Sorooshian, S. (2008).
Hydrological Modelling in Arid and Semi-
Arid Areas. Cambridge University Press.
[3] Chow, V. T., Maidment, D. R., & Mays, L.
W. (1988). Applied Hydrology. McGraw-Hill.
[4] Shortridge, J. E., & Guikema, S. D. (2016).
Machine Learning Methods for Hydrologic
Flood Forecasting: A Review. Environmental
Modelling & Software, 83, 214-228.
[5] Mosavi, A., Ozturk, P., & Chau, K. W.
(2018). Flood Prediction Using Machine
Learning Models: Literature Review.
Water, 10(11), 1536.