
1
Đ nh nghĩaị
Bi u đ mômen xo nể ồ ắ
ng su t trên m t c t ngang c a thanh tròn Ứ ấ ặ ắ ủ
ch u xo n thu n túyị ắ ầ
Bi n d ng c a thanh tròn ch u xo nế ạ ủ ị ắ
Tính toán đ b n c a thanh ch u xo nộ ề ủ ị ắ
Tính toán đ c ng c a thanh ch u xo nộ ứ ủ ị ắ
Tính lò xo hình tr có b c ng n ch u kéo – nénụ ướ ắ ị
Bài toán siêu tĩnh
XO N THANH TRÒNẮ
2
Đ nh nghĩaị
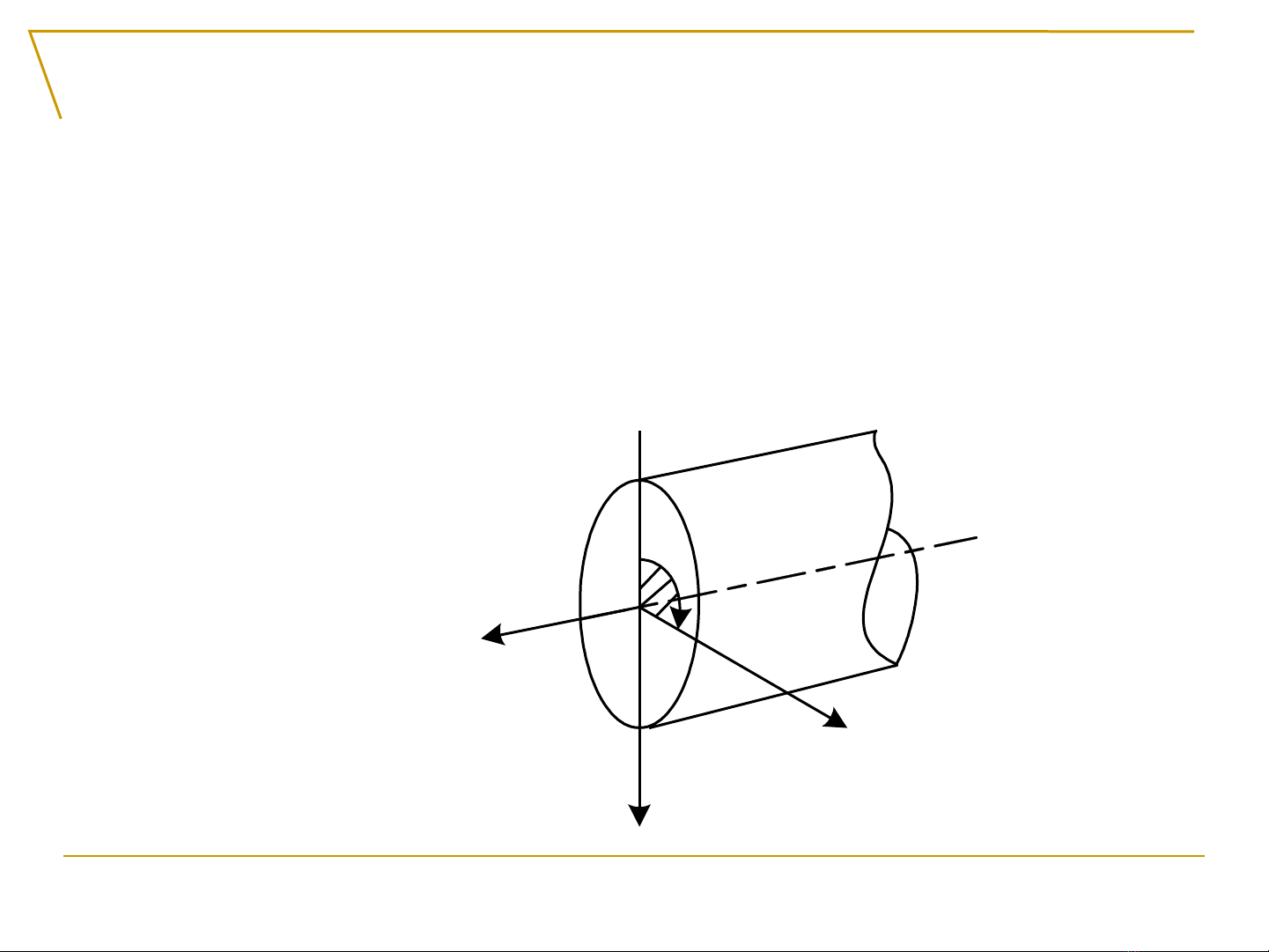
Thanh đ c g i là ch u xo n thu n túy khi ượ ọ ị ắ ầ
trên m i m t c t ngang ch có m t thành ọ ặ ắ ỉ ộ
ph n n i l c là mômen xo n Mầ ộ ự ắ z
y
x
z
Mz
3
AB C D E
ABC D E
A B C D E
4
Bi u đ mômen xo nể ồ ắ
Mômen xo n n i l cắ ộ ự
Quy t c tính n i l cắ ộ ự
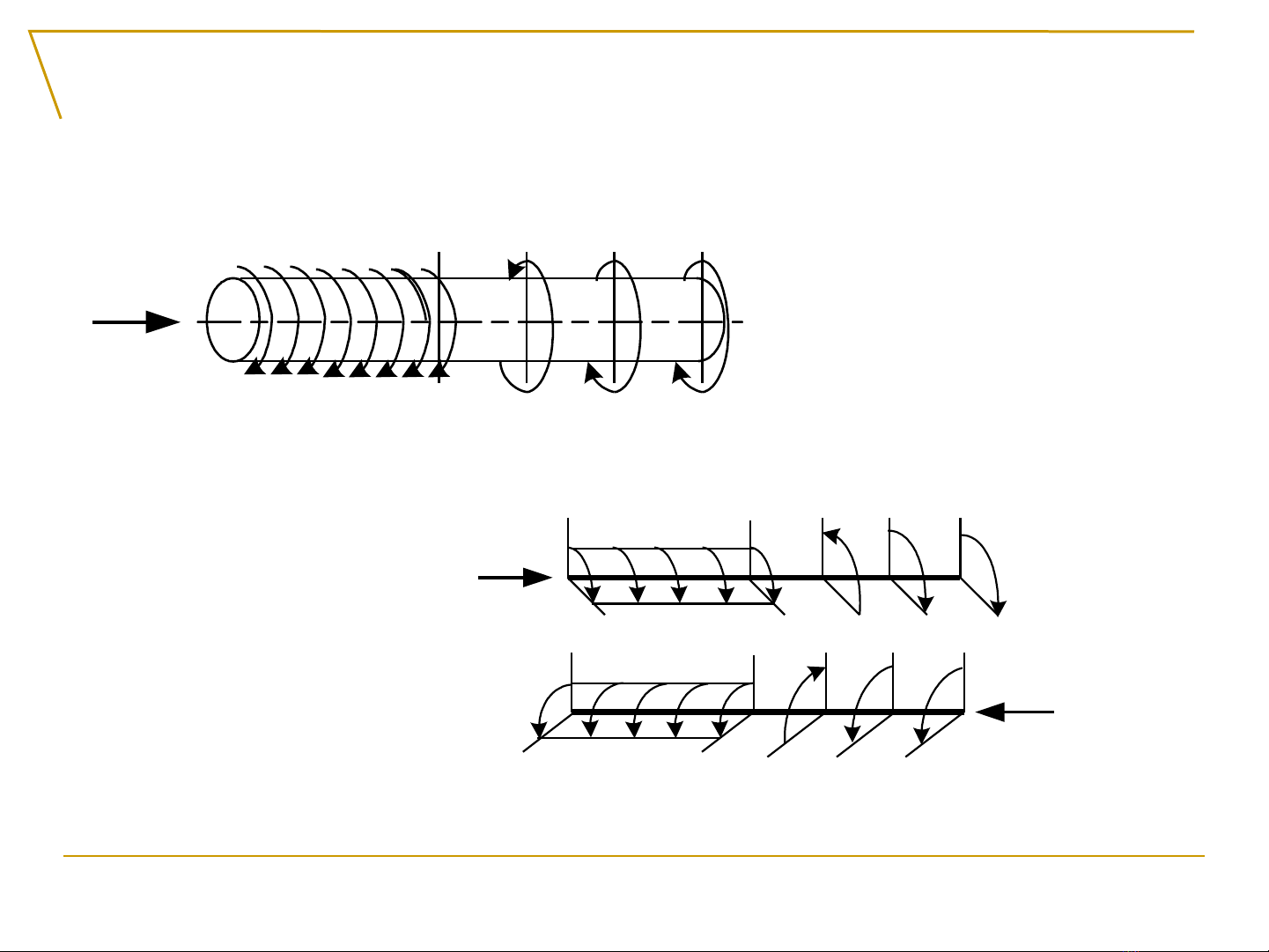
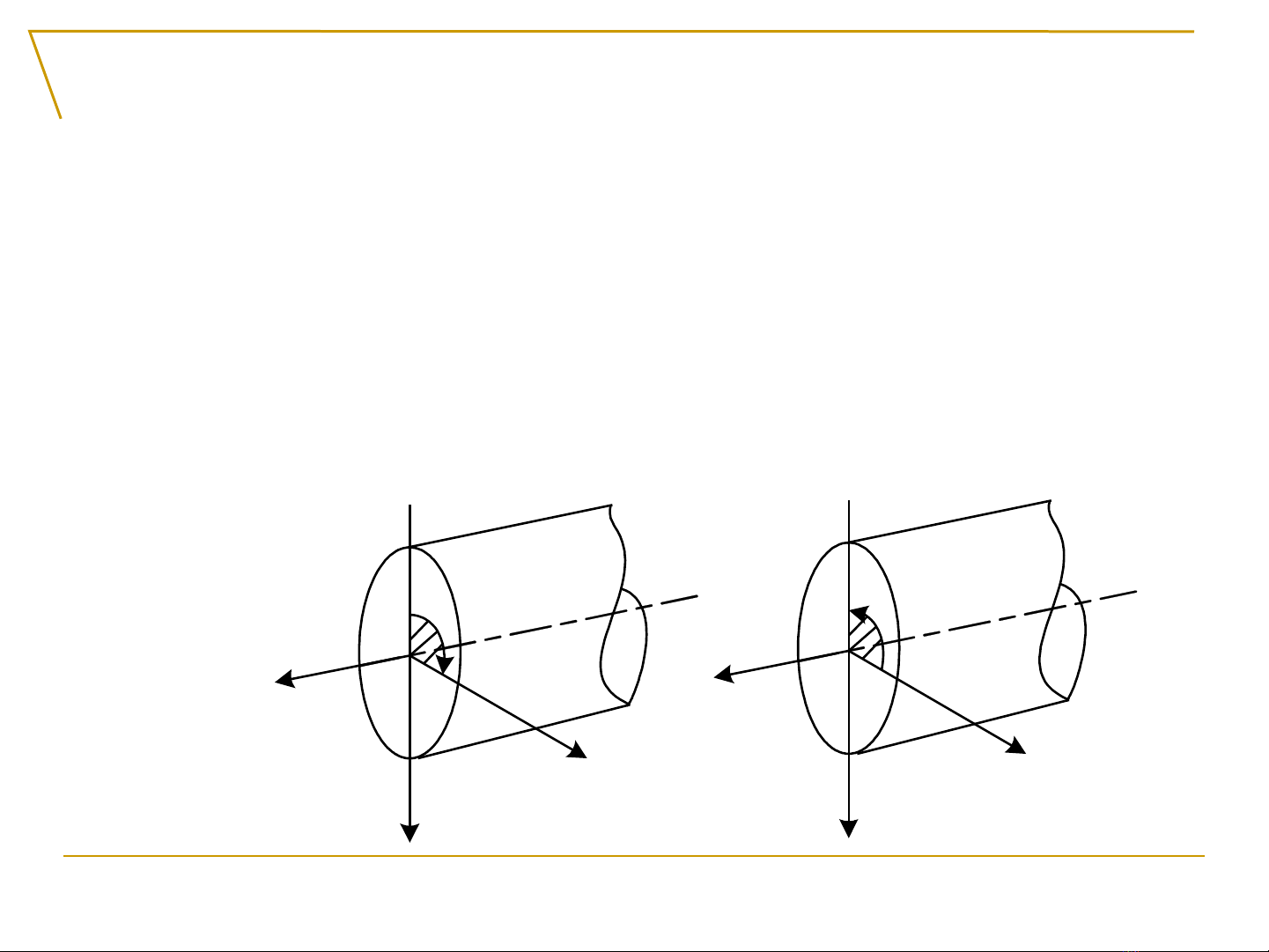
Quy c d u:ướ ấ Mz d ng khi ươ nhìn t ngoàiừ vào m t c t ặ ắ
th y chi u quay c a nó ấ ề ủ thu n chi u kim đ ng hậ ề ồ ồ, và
có d u âm khi có chi u quay ng c l iấ ề ượ ạ
( )
∫
∑
+=
bên1
z
bên1
izz
dzmPmM
y
x
z
Mz
y
x
z
Mz
5
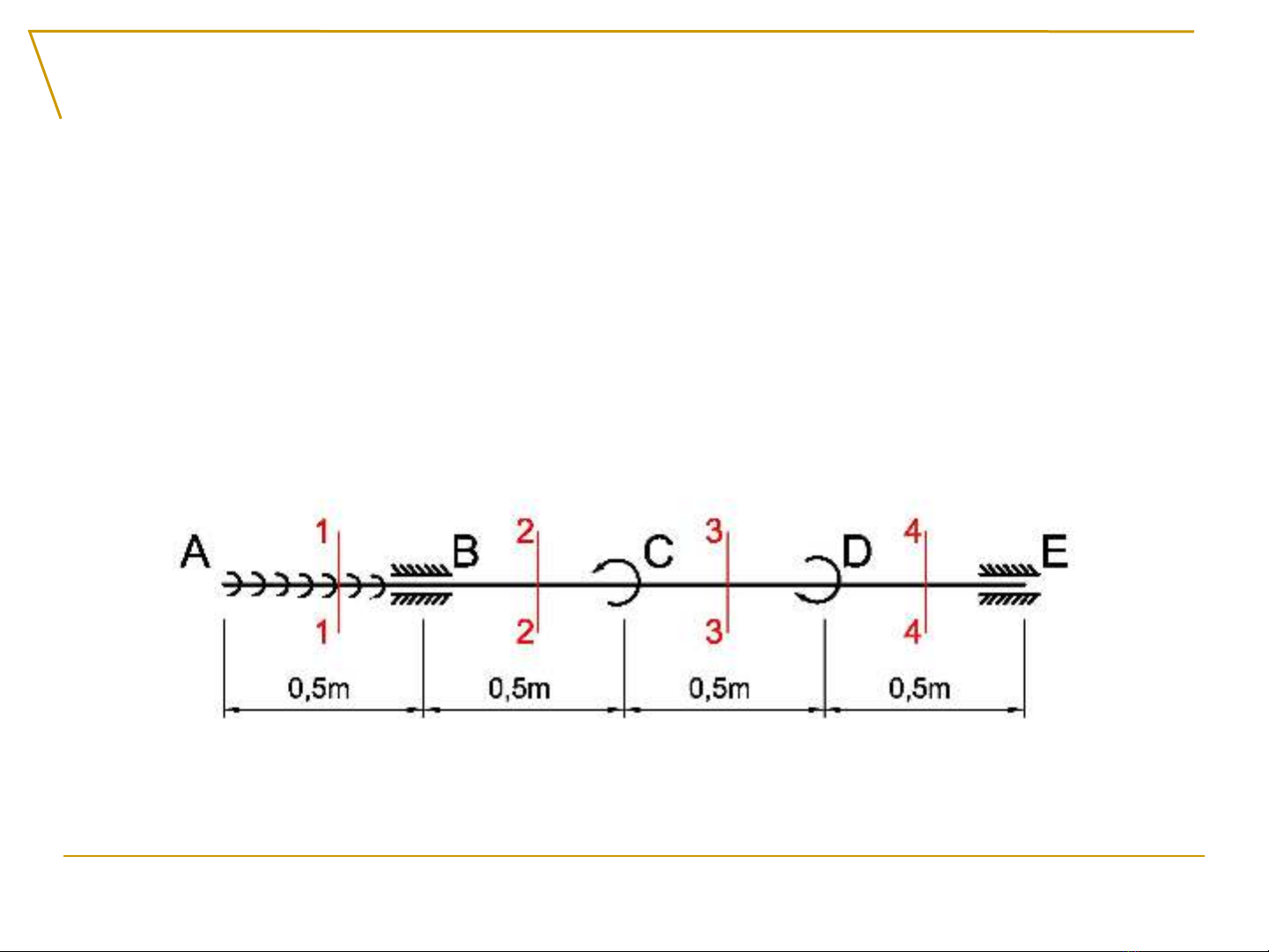
Ví d 6.1ụ
V bi u đ n i l c c a thanh ch u xo n d i ẽ ể ồ ộ ự ủ ị ắ ướ
tác d ng c a các ngo i l c ụ ủ ạ ự


























