SỞ GD & ĐT THỪA THIÊN HUẾ KIỂM TRA HỌC KÌ I NĂM HỌC 2008-2009
TT GDTX HƯƠNG THUỶ Môn: TOÁN- LỚP 12
Thời gian làm bài: 90 phút
Câu I: (3 điểm)
Cho hàm số 3 2
3 1
y x x
(C)
1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2. Viết phương trình tiếp tuyến với (C) tại điểm M(3;1)
Câu II: (2 điểm)
1. Tính giá trị của biểu thức
1 3 3
3
log 7 2log 49 log 27
P
2. Tìm giá trị lớn nhất của hàm số
2 1
3
x
y
x
trên đoạn
0;2
Câu III: (2 điểm)
1. Giải phương trình 2 1
9 10.3 1 0
x x
2. Giải bất phương trình 2
3
1
3
log (x x 6) log 3x 0
Câu III: (3 điểm)
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc tạo bởi cạnh bên và
mặt đáy bằng 600 .
1. Tính thể tích khối chóp S.ABCD.
2. Xác định tâm và bán kính mặt cầu đi qua 5 điểm S, A, B, C, D.
--------------------HẾT--------------------
SỞ GD & ĐT THỪA THIÊN HUẾ KIỂM TRA HỌC KÌ I NĂM HỌC 2008-2009
TT GDTX HƯƠNG THUỶ Môn: TOÁN- LỚP 12
Thời gian làm bài: 90 phút
ĐÁP ÁN VÀ THANG ĐIỂM
Câu I Nội dung Điểm
3 điểm a.Khảo sát hàm số
TXĐ:
D R
Sự biến thiên: 2
' 3 6
y x x
2
' 0 3 6 0
0
2
y x x
x
x
Hàm số đồng biến trên khoảng
;0 ; 2;
 
Hàm số nghịch biến trên khoảng
0; 2
Hàm số đạt cực đại tại x = 0, yCĐ = -1
Hàm số đạt cực tiểu tại x = 2, yCT = -3
3 2
lim 3 1
xx x


3 2
lim 3 1
xx x


Bảng biến thiên
x

0 2

y
+ 0
0 +
y
1

-3
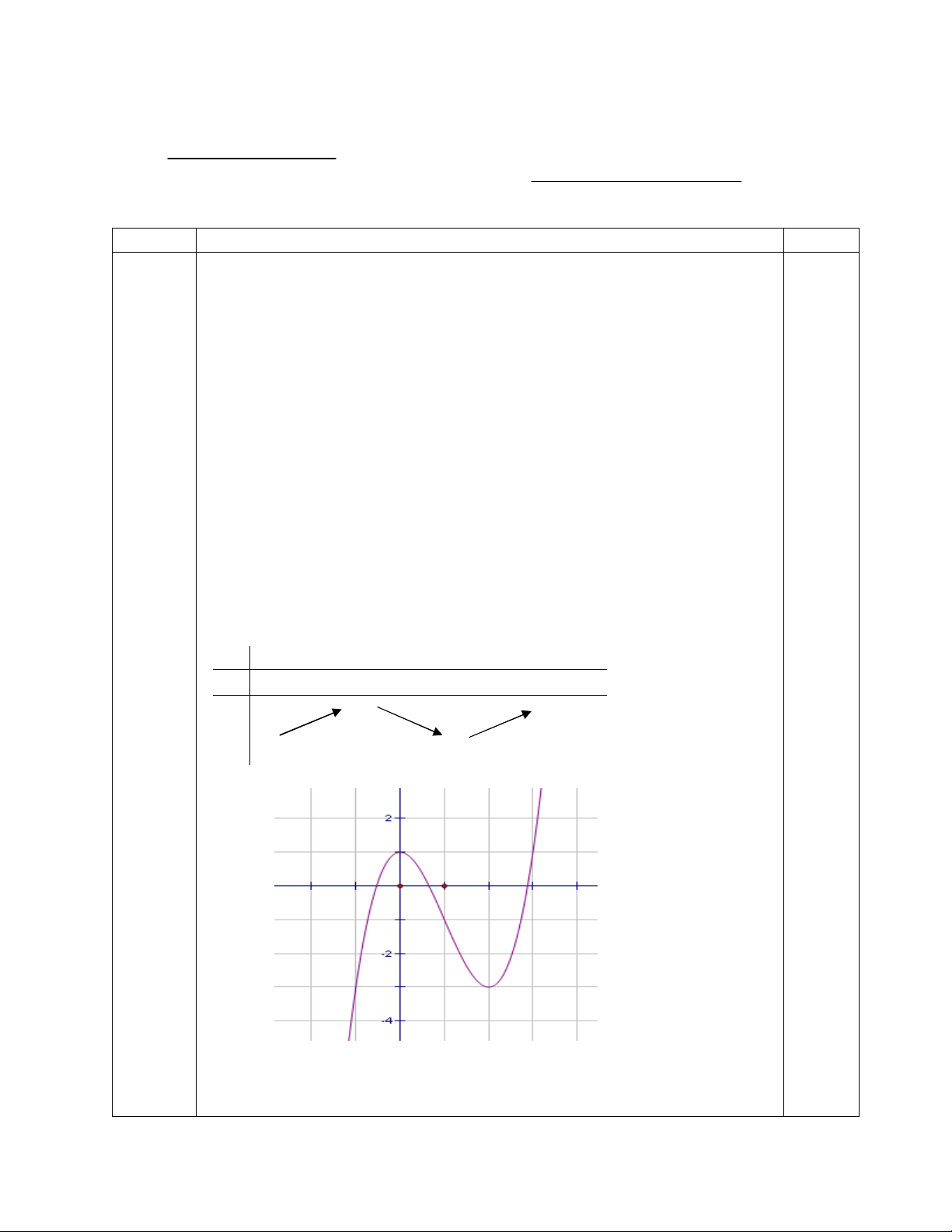
Đồ thị: đồ thị hàm số cắt trục tung tại điểm (0;-1)
b. Ta có M(3;1)
(C) nên phương trình tiếp tuyến tại M có dạng
0 0 0
'( )( )
y y f x x x
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
Mà
'(3) 9
f
Suy ra phương trình tiếp tuyến tại M
1 9( 3)
y x
9 26
y x
0,25
0,5
Câu II
2 điểm a. 1 3 3
3
log 7 2log 49 log 27
P
2 3
3 3 3
3 3
3
log 7 2log 7 2log 3
log 7 4log 7 6
3log 7 6
b. Ta có
2 1
3
x
y
x
TXĐ
\ 3
D R
2
5
' 0,
( 3)
y x D
x
Hàm số nghịch biến trên D nên hàm số nghịch biến trên
0; 2
Suy ra
1
axy= y(0)=
3
m
0,5
0,25
0,25
0,25
0,25
0,25
0,25
Câu III
2 điểm a. 2 1
9 10.3 1 0
x x
1 1
9.9 10.3 1 0
x x
(*)
Đặt 1
3 , 0
x
t t
Phương trình (*) trở thành
2
9 10 1 0
t t
1
1
9
t
t
Với 1
1 3 1 1 0 1
x
t x x
Với 1
1 1
3 1 2 3
9 9
x
t x x
Vậy nghiệm của phương trình cho là x = -1; x =-3.
b. 2
3
1
3
log (x x 6) log 3x 0
(*)
Đk
26 0
3
3 0
x x x
x
Bất phương trình (*) trở thành
0,25
0,25
0,25
0,25
0,25
2
3
1
3
log (x x 6) log 3x 0
2
3 3
log 3 log ( 6)
x x x
Vì cơ số 3 > 1 nên bất phương trình trên tương đương với bất
phương trình 2
3 6
x x x
2
4 6 0
x x
2 10 2 10
x
Vậy nghiệm của bất phương trình là
3 2 10
x
0,25
0,25
0,25
Câu IV
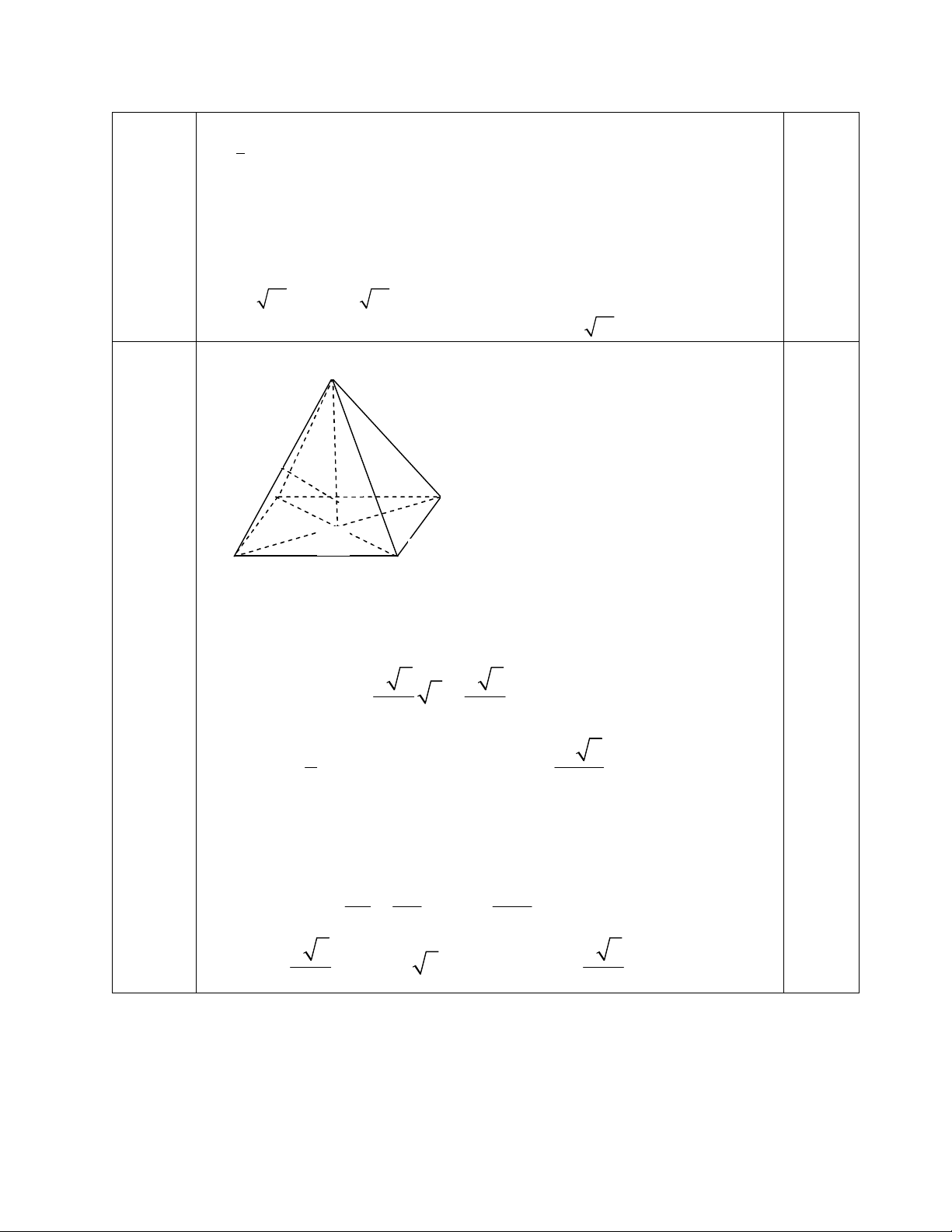
3 điểm
Hình vẽ
Đường cao của hình chóp là SO
Ta có (SA. ABCD) = (SA,AC) =
฀
SAC
= 600
- SO = AO tan600 =
2 6
3
2 2
a a
1
. ( )
3
SABCD
V SO dt ABCD
3
6
6
SABCD
a
V
b.Ta có mọi điểm thuộc SO cách đều A, B, C, D.
Gọi K là trung điểm của SA, trong mp(SAC) dựng trung trực của SA
cắt SO tại I. Suy ra I là tâm mặt cầu đi qua 5 điểm S, A, B, C, D.
Ta có R = SI mà
2
2
SI SK SA
SI
SA SO SO
Với SO =
6
2
a , SA =
2
a
6
3
a
R SI
0,5
1
1
0,5
Những bài toán có nhiều cách giải thì chấm theo cách giải của học sinh.
S
A
B
C
D
O
K
I
SỞ GD&ĐT BÌNH PHƯỚC ĐỀ THI HỌC KÌ I NĂM HỌC 2009-2010
ĐỀ CHÍNH THỨC MÔN TOÁN
Thời gian:150 phút, (không kể thời gian phát đề)
I. PHẦN CHUNG CHO TẤT CẢ THÍ SINH ( 7 điểm).
Câu 1 ( 3,5 điểm) Cho hàm số y = x3 – mx + m – 2
1. Định m để hàm số có cực đại và cực tiểu.
2. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số khi m = 3.
3. Biện luận theo tham số k số nghiệm của phương trình:
x3 – 3x – k + 2 = 0.
Câu 2 ( 1,5 điểm) Giải các phương trình và bất phương trình sau:
1. ln(x-4) = 5 – x
2. 32x+2 - 4.3x+2 + 27 > 0.
Câu 3 ( 2 điểm) Cho hình chóp S.ABC, đáy ABC là tam giác vuông cân tại B,
cạnh AB = a. Biết SA vuông góc với đáy ABC và SA = 2a.
1. Tính thể tích khối chóp.
2. Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC.
II. PHẦN RIÊNG ( 3 điểm)
1. Theo chương trình chuẩn.
Câu 4a ( 2 điểm)
1. Viết phưng trình tiếp tuyến với đồ thị hàm số y = x3 – 3x2 + 4 tại điểm A có
hoành độ bằng – 1.
2. Định m để hàm số mx
y
x m
1
luôn giảm trên từng khoản xác định.
Câu 5b ( 1 điểm) Tính giá trị lớn nhất , giá trị nhỏ nhất của hàm số
y = sin2x – x trên đoạn
;
2 2
2. Theo chương trình nâng cao:
Câu 4b ( 2 điểm)
1. Cho hàm số
x x
f x ln e e
2
1. Tính f’(ln2)
2. Tính giá trị lớn nhất, nhỏ nhất của hàm số
y x x
1 2 .
Câu 5b ( 1 điểm) Tìm m để phương trình sau có duy nhất một nghiệm
log x log x m
2 2
3 3
1 2 1 0
HẾT