ĐỀ 4
( Thời gian làm bài 90 phút )
Câu I ( 1,0 điểm )
Cho cấp số nhân (
n
u
) có 4 6
3 5
u u 120
u u 60
.Xác định số hạng đầu và công bội của cấp số nhân .
Câu II ( 3,0 điểm )
a. Chứng minh rằng dãy số (
n
u
) với 2
n
2
n 1
u
2n
là một dãy số giảm và bị chặn .
b. Tìm giới hạn sau : 2
x 2
lim x 2
c. Cho hàm số 2
ax 2
f (x)
n 2
nÕu x
2x 1 Õu x .Tìm giá trị của a để hàm số f(x) liên tục trên
฀
.
Câu III ( 3,0 điểm )
a. Tìm đạo hàm của hàm số
3
y tan x
.
b. Tính gần đúng giá trị
sin 29
.
c. Chứng minh rằng phương trình 2
cos x x
= 0 có ít nhất một nghiệm .
Câu IV ( 3,0 điểm )
Cho hình lăng trụ ABC.A’B’C’ có ABC là tam giác đều cạnh a , AA’ vuông góc với mặt phẳng
(ABC) và AA’ =
a 2
2
. Gọi O và O’ lần lượt là trung điểm của AB và A’B’ .
a. Chứng minh rằng : AB
mp(COO’) .
b. Tính khoảng cách giữa hai đường thẳng AB và CB’ .
. . . . . . . .Hết . . . . . . .
HƯỚNG DẪN
Câu I ( 1,0 điểm )
Gọi
1
u
là số hạng đầu , q là công bội của cấp số nhân .
Áp dụng công thức :
n 1
n 1
u u .q
, ta có :
3 5 3 2
1 1 1
4 6
2 4 2 2
3 5 1 1 1
u .q u .q 120 u .q (1 q ) 120 (1)
u u 120
u u 60
u .q u .q 60 u .q (1 q ) 60 (2)
Lấy (1) chia (2) , ta được :
q 2
. Thay
q 2
vào (2) : 2
1 1
u .q (1 4) 60 u 3
Vậy cấp số nhân này có 1
u 3, q 2
.
Câu II ( 3,0 điểm )
a. ( 1đ ) Ta có : n
2
1 1
u2
2n
. Suy ra :
+ n 1 n 2 2 2 2
1 1 1 1 1 1
u u ( ) ( ) 0, n 1
2 2
2(n 1) 2n 2(n 1) 2n
. Suy ra (
n
u
) là dãy số giảm .
+ Vì n
1u 1
2
, n 1
nên (
n
u
) là một dãy số bị chặn .
b. (1đ ) 22 2
2 2 2
x 2 x 2 x 2 x 2
x 5 3
x 5 9 x 4 x 2 2
lim lim lim lim
x 2 3
(x 2)( x 5 3) (x 2)( x 5 3) x 5 3
c. (1đ) Tập xác định D =
฀
+ Nếu
x 2
thì
2
f (x) ax
là hàm số liên tục trên
( ;2)

+ Nếu
x 2
thì
f (x) 2x 1
là hàm đa thức nên liên tục trên
(2; )

Do đó : hàm số f(x) liên tục trên
฀
hàm số f(x) liên tục tại điểm x = 2
2
x 2 x 2 x 2 x 2
3
lim f (x) lim f (x) f (2) lim (2x 1) lim ax 3 4a a
4
Vậy với
3
a
4
hàm số đã cho liên tục
฀
Câu III ( 3,0 điểm )
a. (1đ) Ta có :
3 3 2
2 2 2
3 3
3. tan x
1 1 1 1 1
y tan x y' .(tan x)' .3tan x. .3tan x.
2 tan x
cos x cos x 2cos x
2 tan x 2 tan x
b. (1,5đ) Áp dụng công thức : o o o
f '(x x) f (x ) f '(x ). x
Phân tích :
29 30 1 ( )
6 180
. Chọn : o
x , x =
6 180

Đặt f(x) = sinx , ta có :
1 3
f '(x) cosx , f( ) sin , f '( ) cos
6 6 2 6 6 2
Suy ra : 1 3
sin 29 sin[ ( )] f[ ( )] f ( ) f '( ).( ) . 0, 4848
6 180 6 180 6 6 180 2 2 180

Vậy :
sin 29 0,9954
c) (0,5đ) Xét hàm số : f(x) = 2
cos x x
liên tục khi
x 0
.
Ta có : f(0) = 1 , f(
2
) =
2
< 0 nên đã cho có ít nhất một nghiệm .
Câu IV ( 3,0 điểm )
a. (1đ) Ta có :
ABC đều nên AB
CO .
Mặt khác :
AB OO'
. Vì OO’ // AA’ và AA’
(ABC)
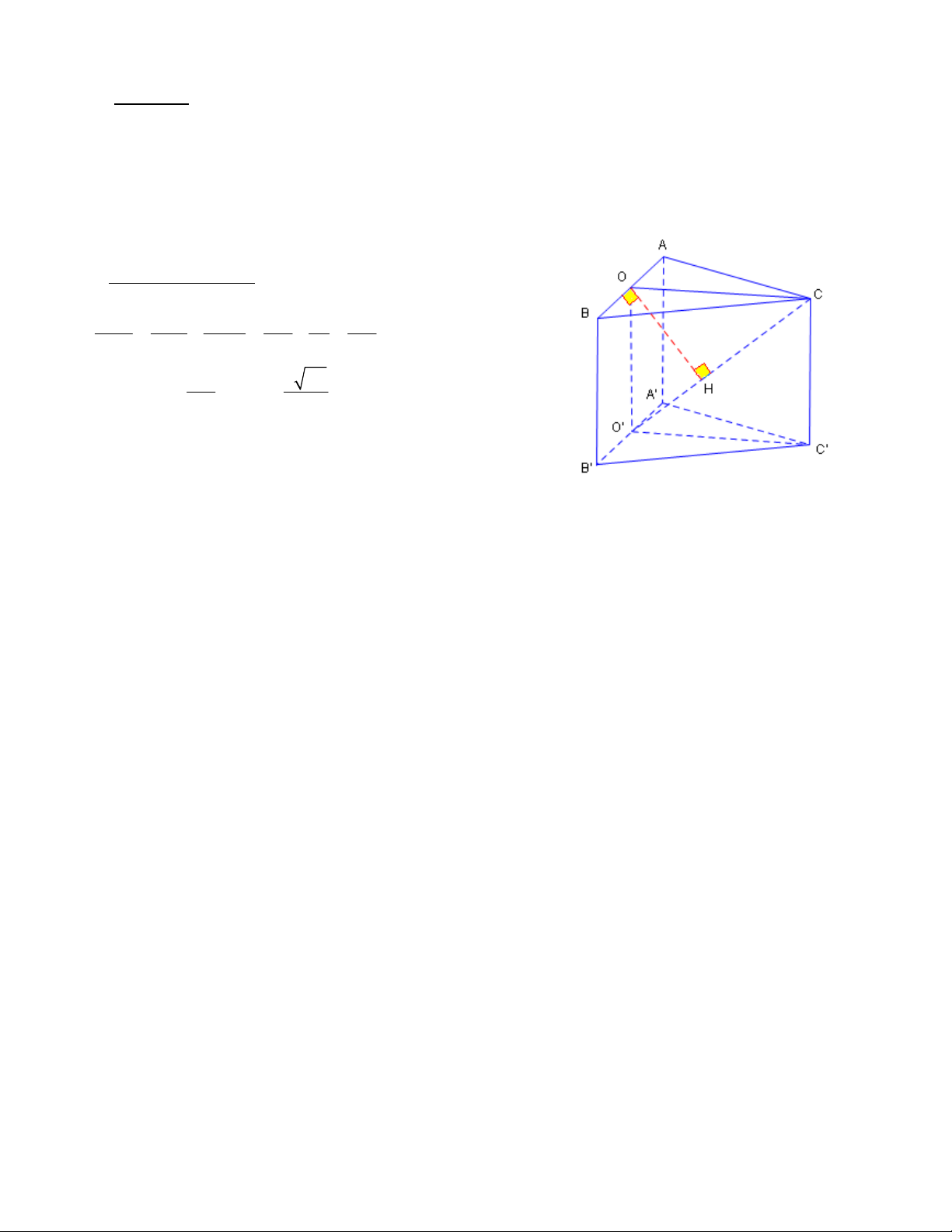
Suy ra :
AB (COO')
b. (2đ)
+ Xác định :
Ta có (CB’O’) chứa CB’ và song song với AB .
Do đó : Khoảng cách giữa AB và CB’ bằng khoảng cách giữa AB và (CB’C’) .
Vậy : d[AB;CB’] = d[AB,(CB’O’)] = d [O, (CB’O’)]
Ta có : AB (COO') ( câu 1)
O'B' (COO') (CO'B') (COO')
O'B' // (COO')
Do đó khi kẻ OH
O’C thì OH
(CO’B’) ,
H (COO')
+ Tính khoảng cách :
Tam giác COO’ vuông tại O . có đường cao là OH nên
2 2 2 2 2 2
2
2
1 1 1 4 2 10
OH OC OO' 3a a 3a
a 30
3a
OH OH
10 10
- 1 -
KIỂM TRA 1 TIẾT GIẢI TÍCH 11- Đề 1
Câu1: Tính đạo hàm của hàm số sau (5đ)
5 2
) 3 4
a y x x t
với t: hằng số
2
) 1 2 7
b y x x
3 2
) sin 5 10
c y x x
Câu 2: Cho hàm số
3 2
2
x
y f x
x
có đồ thị (C). Viết phương trình tiếp tuyến của đồ thị (C), biết
rằng tiếp tuyến song song với đường thẳng d:
8 2013
y x
. (3đ)
Câu 3: Giải bất phương trình sau
' 0
y
với 2
4 9
4
x x
y
x
(2đ)
- 2 -
Đáp án:
Câu Đề Điểm
1 Tính đạo hàm của hàm số sau (5đ)
5 2
) 3 4
a y x x t
với t: hằng số
2
) 1 2 7
b y x x
3 2
) sin 5 10
c y x x
5 2
) 3 4
a y x x t
với t: hằng số
4
4
' 3.5 2
y x
x
0,75đ
4
2
' 15y x
x
0,25đ
2
) 1 2 7
b y x x
'
'
2 2
' 1 2 7 1 2 7
y x x x x
0,75đ
2
2 7 '
' 2 . 2 7 1 .
2 2 7
x
y x x x x
0,75đ
2
1
' 2 . 2 7
2 7
x
y x x x
0,5đ
3 2
) sin 5 10
c y x x
'
2 2 2
' 3sin 5 10 . sin 5 10
y x x x x 0,75đ
2 2 2 2
' 3sin 5 10 . os 5 10 . 5 10 '
y x x c x x x x 0,75đ
2 2 2
' 3sin 5 10 . os 5 10 . 2 5
y x x c x x x
0,5đ
2 Cho hàm số
3 2
2
x
y f x
x
có đồ thị (C). Viết phương trình tiếp tuyến của
đồ thị (C), biết rằng tiếp tuyến song song với đường thẳng d:
8 2013
y x
.
(3đ)
Do tiếp tuyến song song với đường thẳng d:
8 2013
y x
nên tiếp tuyến có
hệ số góc là
8
k
0,5đ
Gọi
0 0
;
M x y
là tiếp điểm 0,25đ
Ta có
2
8
'
2
f x
x
0,5đ
Và
02
0
8
' 8
2
f x
x
0,25đ
2
0
8 8 2
x
0
2
0 0
0
1
4 3 0
3
x
x x x
0,25đ
Với 0
1
x
;
0
' 8
f x
0
1 5
y f
0,25đ