1
ĐỀ ÔN SỐ 1
Câu 1: Cho 2
u i j
và
v i x j
. Xác định x sao cho
u
và
cùng phương.
A.
1
.
2
x B.
1
.
4
x
C.
1
x. D.
2.
x
Câu 2: Cho tập hợp:
2
| 2 5 0
A x x x
. Chọn đáp án đúng:
A. A = 0. B. A = 0. C. A = . D. A = .
Câu 3: Tập nghiệm của phương trình
2 2
5 5
x x x x
là:
A.
0
S. B. S
. C.
5
S. D.
0;5
S.
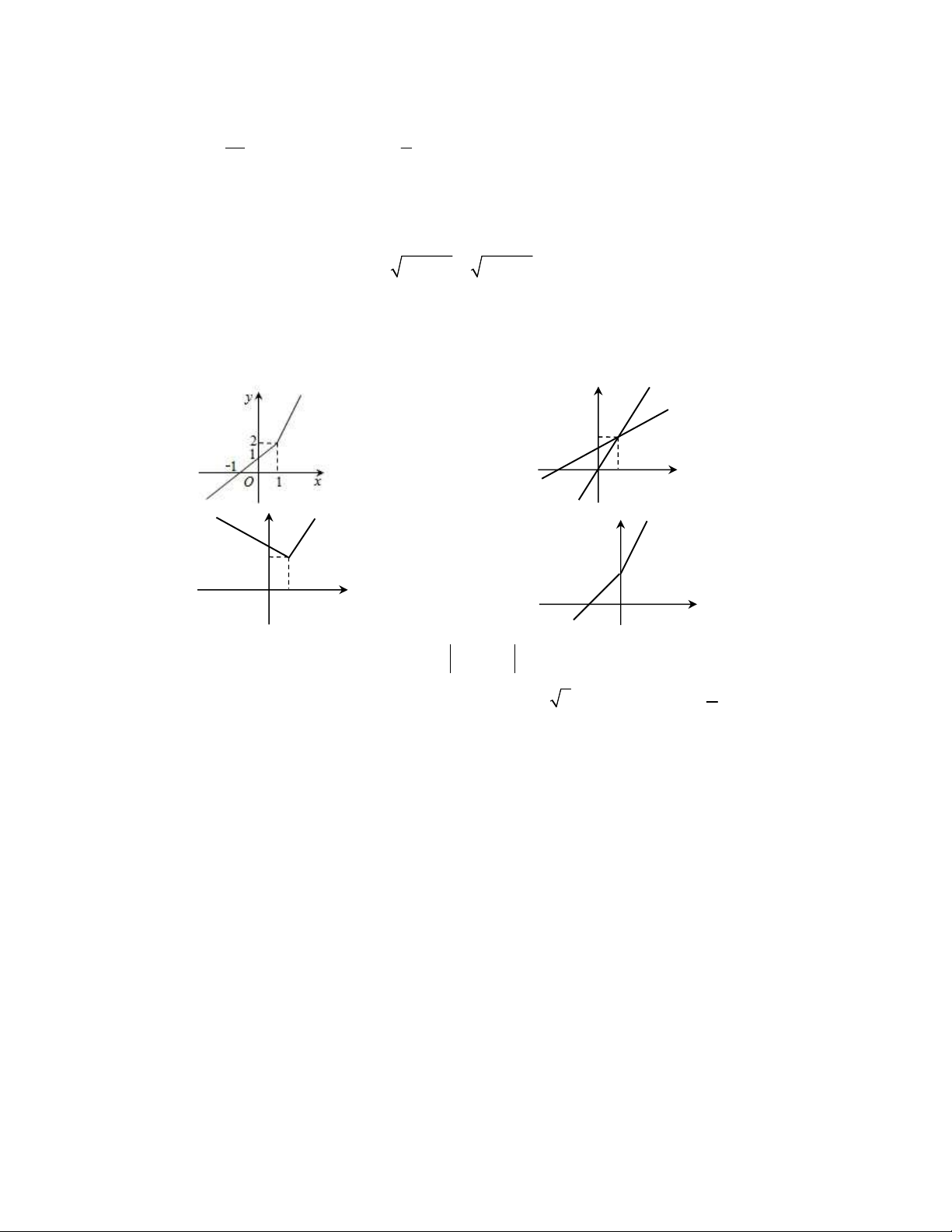
Câu 4: Hàm số
1 khi 1
2 khi 1
x x
x x
y
có đồ thị:
A. . B. .
C. . D. .
Câu 5: Cho hình vuông
ABCD
cạnh
a
. Tính
BA BC
theo
:
A.
a
. B.
2
a
. C.
2
a
. D.
2
a
.
Câu 6: Trong mặt phẳng
Oxy
, cho
0;6
A,
1;3 ,
B
4;2
C. Một điểm
D
có tọa độ thỏa mãn
2 3 0
AD BD CD
. Tọa độ điểm
D
là
A.
5;3 .
B.
3;5
. C.
5;3 .
D.
3;5 .
Câu 7: Trong ngày hội mua sắm trực tuyến Online Friday, cửa hàng T đã tiến hành giảm giá và bán
đồng giá nhiều sản phẩm. Các loại áo bán đồng giá x (đồng), các loại mũ bán đồng giá y
(đồng), các loại túi xách bán đồng giá z (đồng). Ba người bạn Nga, Lan, Hòa đã cùng nhau mua
sắm trực tuyến tại của hàng T. Nga mua 2 chiếc áo, 1 mũ, 3 túi xách hết 1450000 (đồng); Lan
mua 1 chiếc áo, 2 mũ, 1 túi xách hết 1050000 (đồng); Hòa mua 3 chiếc áo, 2 túi xách hết
1100000 (đồng). Hỏi x, y, z lần lượt là bao nhiêu?
A.
150000;250000;350000.
B.
300000;300000;250000.
C.
200000;250000;250000.
D.
200000;300000;250000.
Câu 8: Có bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
5;5
để phương trình
2
4 2
m x m m
có nghiệm duy nhất?
A.
9
. B.
10
. C.
. D.
11
.
x
y
O
1
2
x
y
O
1
2
x
y
O
2
2
2
Câu 9: Phương trình
1 2 1
1 1
x
x
x x
có bao nhiêu nghiệm?
A. Vô số nghiệm. B.
0
. C.
1
. D.
2
.
Câu 10: Tập xác định của hàm số
3 4
1
x
y
x
là:
A.
\ 1
. B.
. C.
1;
. D.
1;

.
Câu 11: Trong mặt phẳng
Oxy
, cho tam giác
ABC
có trung điểm của cạnh
BC
là
2;1
M và trọng
tâm tam giác là
1;3
G. Tọa độ đỉnh
A
của tam giác là:
A.
4;7
. B.
2;4
. C.
7;7
. D.
4;5
.
Câu 12: Tập nghiệm của hệ phương trình
2 5 1
4 7
x y
x y
là:
A.
{(3, 1)}
. B.
(3, 1)
. C.
{3, 1}
. D.
3, 1
.
Câu 13: Biết parabol 2
ax bx c
y
đi qua gốc tọa độ và có đỉnh là I (–1; –3). Giá trị của a, b, c là:
A. a = 3, b = –6, c = 0. B. a = 3, b = 6, c = 0.
C. a = – 3, b = 6, c = 0. D. a = -1, b = 0, c = 3.
Câu 14: Cho 2 phương trình 2
1 0
x x
(1) và
1 2
x x
(2)
Khẳng định đúng nhất trong các khẳng định sau là:
A. (1) và (2) tương đương.
B. Phương trình (1) là hệ quả của phương trình (2).
C. Phương trình (2) là hệ quả của phương trình (1).
D. Cả A, B, C đều đúng.
Câu 15: Cho phương trình bậc hai:
2 2
2 2 12 0
x k x k
. Giá trị nguyên nhỏ nhất của tham số
k
để phương trình có hai nghiệm phân biệt là:
A.
1
k
. B.
2
k
. C.
3
k
. D.
4
k
.
Câu 16: Cho
4;1 , 5; , ; 2
E F G

. Chọn khẳng định đúng
A.
4;E F
. B. F G
. C.
4; 2
E G
. D.
;F G
 
.
Câu 17: Parabol 2
3 2 1
y x x
có trục đối xứng là đường thẳng:
A.
4
3
y
. B.
1
3
y
. C.
4
3
x
. D.
1
3
x
.
Câu 18: Cho hàm số 2
4 2017
2xxy
. Khẳng định định sau đây, khẳng định nào đúng ?
A. Hàm số nghịch biến trên và đồng biến trên .
B. Hàm số đồng biến trên và nghịch biến trên .
C. Hàm số đồng biến trên và nghịch biến trên .
D. Hàm số nghịch biến trên và đồng biến trên .
Câu 19: Đồ thị của hàm số
ax b
y
đi qua các điểm
1
0; 1 , ;0 .
5
A B
Giá trị của
,
a b
là
A.
1; –5.
a b
B.
5; –1.
a b
C.
1; 1.
a b
D.
0; –1.
a b
1;
 ;1
2;

;2
1;
 ;1
2;

;2
3
Câu 20: Tập nghiệm của phương trình
2
1 3 2 0
x x x là
A.
;1
T

. B.
1;2
T
. C.
T
. D.
1
T
.
Câu 21: Cho tam giác
ABC
. Có thể xác định bao nhiêu vectơ (khác vectơ không) có điểm đầu và điểm
cuối là đỉnh
, ,
A B C
?
A.
3.
B.
6.
C. 4. D. 2.
Câu 22: Trong mặt phẳng
Oxy
, cho các điểm
2; 4
A
và
3;1
B. Tìm tọa độ điểm
M
trên
Ox
thỏa
mãn các điểm
, ,
A B M
thẳng hàng.
A.
4;0
. B.
2;0
. C.
1;0
. D.
3;0
.
Câu 23: Cho tam giác
ABC
vuông tại
A
, biết
50
B
. Kẻ đường cao
AH
H BC
, đường phân
giác trong của góc
C
là
CK
K AB
. Xác định góc giữa hai vectơ
AH
và
CK
.
A.
110
. B.
120
. C.
100
. D.
90
.
Câu 24: Số nghiệm của phương trình 2 2
3 5 8 3 5 1 1
x x x x
là
A.
3
. B.
1
. C.
0
. D.
2
.
Câu 25: Cho hình chữ nhật
ABCD
tâm
O
. Trong các khẳng định sau, khẳng định nào đúng?
A.
0.
OA BC DO
 
B.
0.
AB BC BD
 
C.
0.
AC BD CB DA
  
D.
0.
AD DA

TỰ LUẬN
Bai 1. ( 1 điểm) Cho hàm số 2
4 3
y x x
a) Vẽ đồ thị
(P)
của hàm số trên.
b) Biết
(P)
cắt đường thẳng
: 3
d y x
tại hai điểm phân biệt
, .
A B
Tính độ dài đoạn thẳng
.
AB
Bài 2. Giải các phương trình sau :
a) 1 2
1
2 3
x x
x
b)
2 3 4
x x
c)
2 3 1 2
x x
Bài 3. Trong mặt phẳng
Oxy
cho
1; 2
A
,
0;4
B,
3;2
C,
2;0
D.
a) Tìm toạ độ các vectơ
AB

và 3 5
u AB BC
.
b) Tìm toạ độ điểm
G
sao cho
A
là trọng tâm tam giác
BCG
.
c) Tìm toạ độ giao điểm của
AB
,
CD
.
Bài 4. Cho tam giác ABC vuông tại B có
0
30
C. Tính góc giữa 2 vectơ
BA

và
.
AC
Bai 5. Giải phương trình: 2
3 3 2 6 1 7 10 4 3 5 2
x x x x x
ĐỀ ÔN SỐ 2
Bài 1: Cho hai tập hợp
[2; )
A

,
( 1;5]
B
. Tìm:
A B
,
A B
,
A B
,
C
A
.
Bài 2: Cho hàm số
4
( ) 3.
5
f x x
x
Hãy tìm tập xác định của hàm số và tính giá trị của hàm số tại
4
x
.
4
Bài 3:
1) Khảo sát sự biến thiên và vẽ đồ thị
( )
P
của hàm số 2
2 3
y x x
.
2) Tìm giao điểm của
( )
P
với đường thẳng
( ): 1
D y x
.
Bài 4: Giải phương trình 2
2 3 7 3 5
x x x
.
Bài 5: Giải hệ phương trình 2 2
2 1
10 1
x y
x y
.
Bài 6: Cho phương trình 2
( 3) 2( 1) 0
x m x m
(
m
là tham số).
Tìm
m
để phương trình có 2 nghiệm
1
x
,
2
x
thỏa 1 2
2 0
x x
.
Bài 7: Cho
ABC
. Trên các cạnh
AB
,
BC
và
CA
lấy các điểm
D
,
E
,
F
sao cho:
2
DA DB
; 2
EB EC
;
2
FC FA
.
Chứng minh:
AD AE AF AB AC

.
Bài 8: Trong mặt phẳng
Oxy
, cho
ABC
, biết
(4;1)
A,
(1;5)
B,
( 4; 5)
C
.
1) Chứng minh
ABC
vuông tại
A
và tính số đo góc
B
(làm tròn đến phút).
2) Phân giác trong góc
A
cắt cạnh
BC
tại
D
. Gọi
H
là hình chiếu vuông góc của
D
lên
AC
. Tìm tọa
độ của điểm
H
.
ĐỀ ÔN SỐ 3
Câu 1: Cho tam giác
ABC
, trọng tâm
G
, gọi
I
là trung điểm
,
BC M
là điểm thỏa mãn:
2 | | 3| |
MA MB MC MB MC

. Khi đó tập hợp điểm
M
là:
A. Đường trung trực của
IG
. B. Đường tròn tâm
I
, bán kính
BC
.
C. Đường tròn tâm
G
, bán kính
BC
. D. Đường trung trực của
BC
.
Câu 2: Giá trị
2
x
là điều kiện của phương trình nào sau đây?
A. 1
2 0
x x
x
. B. 1
2
4
x x
x
.
C. 1
0
2
xx
. D. 1
2 1
2
x x
x
.
Câu 3: Tìm tất cả các giá trị của
m
để hai đồ thị hàm số 2
2 3
y x x
và 2
y x m
có điểm chung?
A.
7
2
m
. B.
7
2
m
. C.
7
2
m
. D.
7
2
m
.
Câu 4: Cho mệnh đề " 2
, 3 2 0
x x x
". Mệnh đề phủ định của mệnh đề trên là:
A. 2
, 3 2 0
x x x
. B. 2
, 3 2 0
x x x
.
C. 2
, 3 2 0
x x x
. D. 2
, 3 2 0
x x x
.
Câu 5: Một chiếc cổng hình parabol dạng
2
1
2
y x
có chiều rộng
8
d m
. Hãy tính chiều cao
h
của
cồng? (Xem hinh minh họa dưới đây).
5
A. 8h m. B. 9h m. C. 7mh. D. 5mh.
Câu 6: Xác định phương trình của parabol 2
y ax bx c đi qua 3 điểm (0; 1), (1; 1)A B , ( 1;1)?C
A. 21y x x . B. 21y x x . C. 21y x x . D. 21y x x .
Câu 7: Biết rằng đồ thị hàm số y ax b đi qua điểm (2; 1)E và song song với đường thẳng ON với
O là gốc tọa độ và (1;3)N. Tính giá trị biểu thức 2 2
S a b .
A. 40S . B. 58S. C. 4S . D. 58S .
Câu 8: Cho tập hợp (1;5)A và ( ; 1)B m m . Có bao nhiêu giá trị nguyên của m để A giao B là
một khoảng?
A. 5. B. 3. C. 4. D. 2.
Câu 9: Cho hàm số 2 1
( ) 3 2 2
x y
y f x x y
. Giá trị của biểu thức ( 1) (1)P f f là:
A. 2. B. 0. C. 1. D. 4.
Câu 10: Cho
21
: 12 35 0 , : 0 .
7
x
A x x x B x x
Tập \B A là:
A. (1;5) {7}. B. [1;5) {7}. C. (1;5). D. [1;5) .
Câu 11: Véctơ có điểm đầu là A, điểm cuối là B được kí hiệu là:
A. AB . B. AB
. C. | |AB
. D. BA
.
Câu 12: Cho đồ thị hàm số 22 1( )y x x P (hình vẽ sau). Dựa vào đồ thị ( )P xác định số giá trị nguyên
dương của m để phương trình 22 2 2 0x x m có nghiệm [ 1;2]x ?