
KHOA HỌC KỸ THUẬT THỦY LỢI VÀ MÔI TRƯỜNG - SỐ 86 (12/2023)
3
BÀI BÁO KHOA HỌC
ẢNH HƯỞNG CỦA HỆ SỐ MA SÁT GIỮA CÁC HẠT VẬT LIỆU
ĐẾN ỨNG XỬ ỔN ĐỊNH CỦA ĐẬP ĐÁ
Nguyễn Thanh Hải
1
, Võ Thành Trung
2,3
Tóm tắt: Nghiên cứu này sử dụng phương pháp phần tử rời rạc để đánh giá ảnh hưởng của hệ số ma
sát giữa các phần tử đến ứng xử ổn định của kết cấu đập và chân đập đá. Các phần tử có hình dạng đa
giác đều, không bị biến dạng, số lượng các cạnh của đa giác là 5 và cấp phối đường kính hạt được thay
đổi. Hệ số ma sát giữa các hạt vật liệu cấu thành đập được thay đổi từ 0,1 đến 0,9. Kết quả nghiên cứu
cho thấy những ảnh hưởng khác nhau của hệ số ma sát đến các đặc tính dịch chuyển của đập như động
năng trung bình của các khối phần tử, hình thái dịch chuyển của đập, khoảng cách dịch chuyển của các
phần tử sau khi kết cấu bị mất ổn định, cũng như sự ảnh hưởng đến lực tương tác trong quá trình
chuyển động. Đặc biệt, những đặc tính trên của đập bị chi phối mạnh mẽ khi hệ số ma sát giữa các hạt
vật liệu có giá trị nhỏ hơn 0,3, điều này là do sự suy giảm lớn sức kháng cắt so với trọng lượng của đập.
Những kết quả nghiên cứu này là tài liệu tham khảo tin cậy cho các kỹ sư trong việc đánh giá sự ổn định
của đập dựa vào các điều kiện của vật liệu cấu thành.
Từ khóa: Phương pháp phần tử rời rạc, hệ số ma sát, mất ổn định đập, biến dạng đập.
1. ĐẶT VẤN ĐỀ
*
Hiện tượng mất ổn định các đập đất hay đập đá
đổ diễn ra khá phổ biến trong quá trình thi công và
khai thác ở các công trình giao thông và thuỷ lợi
(Chang & Zhang, 2010; Nguyen Van Le, 2009).
Khi xảy ra hiện tượng mất ổn định, các đập đất
hay đập đá đổ dịch chuyển với các vận tốc, cung
trượt và mức độ khác nhau. Những sự mất ổn định
hay phá huỷ này có thể làm ảnh hưởng lớn đến
quá trình thi công, khai thác và sử dụng của các
công trình xây dựng, cũng như có nguy cơ ảnh
hưởng đến sinh kế của người dân ở vùng hạ lưu
của đập. Nghiên cứu tìm hiểu nguyên nhân, cơ chế
vận động, mức độ tác động của hiện tượng mất ổn
định đập cũng như sự ảnh hưởng của các tham số
khác nhau như hình dạng đập, chiều cao đập, vật
liệu và cấp phối cấu thành đập đến các hiện tượng
trên luôn được các nhà khoa học, kỹ sư quan tâm
trong thời gian qua bằng phương pháp thực
nghiệm và mô hình số (Pinyol và nnk., 2008; Bui
1
Khoa Xây dựng Công trình Thuỷ, Trường Đại học Bách
Khoa, Đại học Đà Nẵng, Đà Nẵng, Việt Nam
2
Khoa Cầu đường, Trường Đại học Kiến trúc Đà Nẵng,
Đà Nẵng, Việt Nam
3
Phòng Khoa học Công nghệ, Trường Đại học Kiến trúc
Đà Nẵng, Đà Nẵng, Việt Nam
Truong Son và nnk., 2022). Mặc dù phương pháp
thực nghiệm có ưu điểm là phản ánh tương đối
chính xác sự mất ổn định của đập nhờ vào việc sử
dụng chính xác các nguồn vật liệu đắp đập, dễ
dàng tuân thủ các tiêu chuẩn thi công và nghiệm
thu, nhưng vấn đề tài chính vẫn là trở ngại hàng
đầu đến sự phổ biến của phương pháp, nhất là đối
với các đập có kích thước tương đương với thực
tế. Đồng thời, mô hình thực nghiệm chỉ có khả
năng phản ánh sự thay đổi hình thái của đập mà
không thể nhận biết được các nguyên nhân tiềm
tàng bên trong. Để khắc phục các nhược điểm này,
phương pháp mô hình số được xem là giải pháp
tối ưu vì có khả năng dễ dàng thay đổi mô hình
cũng như các tham số tác động. Ở đó, bài toán có
thể được xem xét ở dạng môi trường liên tục, rời
rạc hoặc kết hợp giữa hai dạng môi trường này.
Trong bài toán xem kết cấu là môi trường liên tục,
các nghiên cứu đánh giá tìm kiếm cung trượt, hệ
số ổn định của kết cấu dưới tác dụng của ngoại lực
thường được khảo sát bằng phương pháp phần tử
hữu hạn (Finite Element method) (Deng và nnk.,
2017; Liu & Wang, 2021). Tuy nhiên giả thiết vật
liệu đất, đá là những dạng vật liệu đồng nhất và
đẳng hướng là hoàn toàn không phù hợp với các

KHOA HỌC KỸ THUẬT THỦY LỢI VÀ MÔI TRƯỜNG - SỐ 86 (12/2023)
4
thí nghiệm X-rays có được (Akimana và nnk.,
2016; Regmi và nnk., 2013). Mặt khác, phương
pháp phần tử hữu hạn chỉ xem xét kết cấu ở biến
dạng nhỏ, điều này dẫn đến việc khó khăn khi
khảo sát sự tác động của đập khi mất ổn định hay
phá hoại. Trái ngược với phương pháp phần tử
hữu hạn, phương pháp phần tử rời rạc (Discrete
Element Method) có khả năng dễ dàng mô tả vật
liệu là các hạt rời rạc, phân bố ngẫu nhiên cả về
kích thước và vị trí. Đặc biệt, phương pháp phần
tử rời rạc có khả năng xác định chính xác lực
tương tác giữa các hạt vật liệu, dẫn đến dễ dàng
khảo sát các đặc tính nội tại bên trong mẫu thí
nghiệm. Thực tế, nhiều nghiên cứu khảo sát sự
mất ổn định của các đập đất, đá hay sự phá hoại
của các cột vật liệu trong các môi trường khác
nhau đã được triển khai bằng phương pháp phần
tử rời rạc, cơ bản cũng đã cung cấp những hiểu
biết ban đầu về cơ chế vận động của các dạng cấu
hình này trong quá trình mất ổn định. Tuy nhiên,
những mô hình nghiên cứu trước đây sử dụng
phương pháp phần tử rời rạc chủ yếu tập trung vào
dạng vật liệu hạt có dạng hình cầu (3D) và hình
tròn (2D) (Lai và nnk., 2021; Mutabaruka và nnk.,
2015). Khi nghiên cứu sự mất ổn định hay phá
hoại của các đập đất, đá bằng dạng vật liệu hình
tròn, sự biến dạng hay dịch chuyển của đập
thường lớn hơn so với thực tế do đặc tính nhẵn và
dễ vận động của các hạt vật liệu. Thực tế, các hạt
vật liệu như đá có các hình dạng và bề mặt gồ ghề
rất khác nhau, điều này cũng gây ra những trở
ngại rất lớn trong việc mô tả chính xác hình dạng
của các hạt đất, đá. Khi đó, hạt vật liệu dạng đa
giác đều là một dạng định nghĩa đơn giản nhưng
có thể khắc phục được các hạn chế của hạt vật liệu
tròn. Khi xét đến phần tử có dạng hình đa giác thì
sự tương tác giữa các phần tử có sự khác biệt, tại
mỗi tương tác lúc này có thể xem xét liên kết đơn
giản như tương tác đỉnh – đỉnh, đỉnh - cạnh hay
phức tạp hơn là cạnh – cạnh giữa các phần tử (D.-
H. Nguyen và nnk., 2014; Nguyen Thanh Hai,
2019). Mỗi dạng tương tác này thể hiện sự ảnh
hưởng rất lớn của độ gồ ghề, hay ma sát giữa
chúng. Ma sát giữa các hạt vật liệu có thể chi phối
lớn đến sự mất ổn định hay vận động của kết cấu
(T.-K. Nguyen & Vo, 2023; Vo và nnk., 2022).
Trong nghiên cứu này, chúng tôi tập trung vào
nghiên cứu sự ảnh hưởng của hệ số ma sát của các
hạt vật liệu đến đặc tính vận động của kết cấu đập
đá trên nền đá bằng phương pháp phần tử rời rạc.
Các phần tử có hình dạng đa giác đều, có số cạnh
là 5 và phần tử hoàn toàn cứng, không bị biến
dạng. Những sự thay đổi về hình dạng kết cấu,
năng lượng của các khối vật liệu cấu thành đập đá,
sự dịch chuyển của các phần tử khi kết cấu bị phá
hủy bởi sự ảnh hưởng của hệ số ma sát được phân
tích cụ thể. Hệ số ma sát được sử dụng từ 0,1 đến
0,9 tương ứng cho 9 trường hợp mô phỏng của kết
cấu đập đá.
2. PHƯƠNG PHÁP SỐ
2.1. Tạo mẫu phần tử đa giác
Mẫu đa giác của các phần tử trong nghiên cứu
có hình dạng là các phần tử đa giác đều, mỗi phần
tử có số lượng 5 cạnh như Hình 1. Việc lựa chọn
phần tử đa giác đều có 5 cạnh để đơn giản hóa
trong việc mô hình hóa các bài toán; dễ dàng xác
định, tính toán các thông số trong mô hình như số
lượng liên kết, quá trình dịch chuyển của các phần
tử cũng như phù hợp với năng lực tính toán của
thiết bị. Các phần tử này nội tiếp đường tròn có
đường kính d = 2R và đại diện cho các vật liệu
cấu thành kết cấu của công trình. Các phần tử này
có khối lượng riêng là (g/cm
3
). Những phần tử
này có kích thước đường kính khác nhau theo tỉ lệ
cấp phối như bảng 1.
Bảng 1. Tỷ lệ hàm lượng các hạt trong mô hình
STT Hàm lượng hạt Kích thước hạt
1 5% d = [0,05 – 0,075]mm
2 20% d = [0,075 – 5]mm
3 75% d = [5 – 800]mm
Để đảm bảo số lượng phần tử phân bổ đồng
đều trong từng loại cấp phối như trên cũng như
đảm bảo quá trình liên kết, thì chúng tôi thực
hiện tạo mẫu ngẫu nhiên trong từng loại cấp
phối đó. Có nghĩa là mỗi cấp phối đều có số các
phần tử có đường kính nhỏ nhất đến lớn nhất
trong từng cấp phối.
2.2. Phương pháp số
Trong bài báo này chúng tôi áp dụng phương
pháp phần tử rời rạc để mô phỏng cho bài toán áp
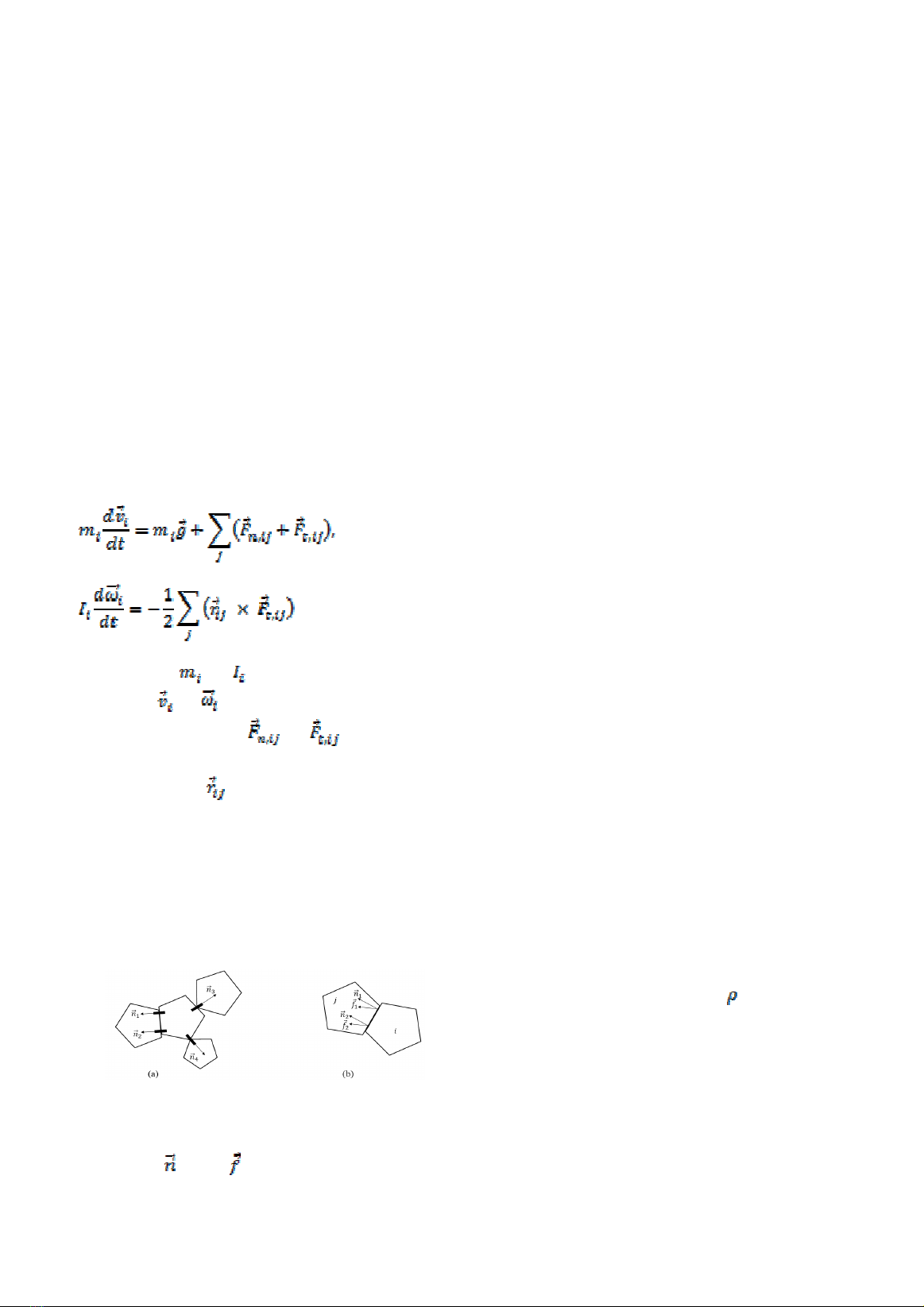
KHOA HỌC KỸ THUẬT THỦY LỢI VÀ MÔI TRƯỜNG - SỐ 86 (12/2023)
5
dụng các phần tử được mô tả ở trên. Phương pháp
phần tử rời rạc được sử dụng phổ biến trong các
bài toán rời rạc như đá, cát, bột
sắt,…(Nezamabadi và nnk., 2017; Radjai &
Dubois, 2011; Vo T.T và nnk., 2018). Các phương
trình chuyển động của các phần tử khi xét có sự
tương tác được phân tích từ các ràng buộc động
học được đặc trưng bởi các thông số như hệ số ma
sát, lực dính giữa các phần tử, sự đàn hồi khi va
chạm. Sự va chạm giữa các phần tử hoàn toàn
cứng trong môi trường rời rạc khi có ngoại lực tác
động cũng như lực tương tác nội tại giữa các phần
tử khi va chạm được tính toán thông qua các định
luật Newton trong bài toán hai chiều. Phương
trình chuyển động của mỗi phần tử khi có va chạm
được xác định theo phương trình (1), (2) dưới đây
(Cundall & St, 1979).
(1)
(2)
Trong đó và là khối lượng và mô men
quán tính, và là véc tơ vận tốc và véc tơ vận
tốc góc của phần tử i. và lần lượt là lực
pháp tuyến và tiếp tuyến tại vị trí va chạm giữa
hai phần tử i, j. là véc tơ chuyển vị nối giữa
tâm của hạt i đến vị trí tiếp xúc giữa hai phần tử i,
j. Các thành phần vận tốc theo các phương, lực
tương tác tiếp tuyến và pháp tuyến của sự va chạm
giữa 2 phần tử tương tác với nhau có thể được xác
định theo Hình (Nezamabadi và nnk., 2017; D. H.
Nguyen và nnk., 2018; Radjai và nnk., 1997).
Hình 1. Một số dạng tương tác đặc trưng giữa
hai phần tử khi va chạm (a) tương tác đỉnh-đỉnh,
đỉnh-cạnh; cạnh-cạnh; (b) xác định véc tơ đơn vị
và lực tại vị trí tiếp xúc
Hình 1 mô tả sự tương tác giữa các phần tử
trong hệ thống khi có sự va chạm cũng như các
đại lượng vô hướng tại các vị trí liên kết. Khi có
tương tác tại các vị trí tiếp xúc giữa 2 phần tử,
chúng tôi xem xét 3 dạng: (i) liên kết đỉnh – đỉnh
(vị trí góc của đa giác); (ii) liên kết đỉnh – cạnh và
(iii) liên kết cạnh - cạnh. Xác định liên kết giữa
hai phần tử đa giác, đối với liên kết đơn giản là
đỉnh - cạnh thì lực pháp tuyến sẽ vuông góc với
cạnh. Khi liên kết là cạnh - cạnh, lúc này xuất hiện
2 véc tơ đơn vị và 2 giá trị lực pháp tuyến, trong
trường hợp này hai giá trị lực có thể được quy đổi
thành một giá trị đại diện cho mỗi liên kết (D. H.
Nguyen và nnk., 2018). Ngoài ra, trường hợp liên
kết giữa hai phần tử chỉ là đỉnh – đỉnh, trường hợp
này thường rất ít khi xảy ra. Nếu trường hợp tiếp
xúc đỉnh – đỉnh tồn tại, một đề xuất xem chúng là
dạng liên kết đơn giản giữa 2 phần tử hoặc liên kết
đỉnh - cạnh hoặc cạnh - cạnh được thực hiện bởi
(D.H. Nguyen & Az, 2015; D. H. Nguyen và nnk.,
2018). Binaree và nnk đã có nghiên cứu khi hệ số
ma sát giữa các phần tử thay đổi từ 0 đến 0,3 nhận
thấy sự khác biệt lớn giữa quan hệ ứng suất – biến
dạng, ứng suất tỷ lệ thuận với việc tăng của hệ số
ma sát. Tuy nhiên khi hệ số ma sát giữa các phần
tử lớn hơn 0,3 thì sự ảnh hưởng này là nhỏ
(Binaree. T và nnk., 2020). Xét cho một tập hợp
mô hình số gồm nhiều phần tử đa giác, khi có sự
liên kết xảy ra trong quá trình va chạm dưới tác
dụng ngoại lực, như được thể hiện ở các Hình 3.
3. MÔ HÌNH NGHIÊN CỨU VÀ CÁC
THAM SỐ
Mô hình nghiên cứu trong bài báo này được
xây dựng theo dạng đập đá có cấp phối hạt nhưng
Bảng 1. Các thành phần cấu thành trong mô hình
là những phần tử đa giác đều như đã trình bày ở
mục 2. Các phần tử này là hoàn toàn cứng, không
bị biến dạng trong quá trình xảy ra tương tác. Các
hạt vật liệu có khối lượng riêng là = 2,5 (g/cm
3
).
Phạm vi của mô hình được xây dựng dựa theo
nghiên cứu của tác giả (Nguyen Thanh Hai, 2019).
Trong nghiên cứu này, mô hình đập đá được chia
thành hai phần, phần thân (granular body) và phần
móng (granular base), như thể hiện ở Hình 2. Bao
quanh bên ngoài là các phần tử không dịch chuyển
(Cluster), các phần tử thuộc Cluster cho phép

KHOA HỌC KỸ THUẬT THỦY LỢI VÀ MÔI TRƯỜNG - SỐ 86 (12/2023)
6
tương tác với các phần tử body và base, tuy nhiên
không cho phép các Cluster này chuyển vị. Tổng
số lượng các phần tử (N) trong mô hình khoảng
hơn 8.000 phần tử, trong đó có 4.261 phần tử cấu
thành khối granular body (N
s
), 3.652 phần tử cấu
thành khối granular base (N
b
), các phần tử còn lại
cấu thành các Cluster.
Hình 2. Mô hình số hai chiều 2D mô tả dạng đập
đá gồm 2 khối body và base được cấu thành từ
các phần tử đa giác đều
Từ khả năng tính toán của tài nguyên máy tính
khi ứng dụng phương pháp phần tử rời rạc trong
bài toán có số lượng phần tử quá lớn, đồng thời
xem xét ứng xử của các khối vật liệu như là thay
đổi hình dạng, quá trình thay đổi năng
lượng,…nên đề xuất mô hình nghiên cứu như
Hình 2. Hình này mô tả mô hình bài toán khảo sát
sự mất ổn định của đập đá, trong đó h
s
= 32 (m),
h
b
= 15 (m) lần lượt là chiều cao thân đập và
móng đập; l = l
1
+ l
2
+ l
3
= 126,4 (m) là chiều dài
tổng thể, l
1
= 43 (m), l
2
= 38,4(m), l
3
= 45 (m) là
chiều dài của các khối.
Trong bài báo này, chúng tôi tập trung nghiên
cứu sự ảnh hưởng của hệ số ma sát giữa các phần
tử để xem xét đến sự ổn định kết cấu chung của
đập. Hệ số ma sát
giữa các phần tử đa giác đều
được đề xuất trong nghiên cứu này nhận các giá trị
lần lượt 0,1; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9.
Hệ số ma sát giữa phần tử thuộc 2 khối body và
base với phần tử Cluster là 0,5 cho toàn bộ 9 mô
phỏng ở trên. Nghiên cứu này chỉ tập trung vào
ứng xử của khối vật liệu, trong trường hợp không
chịu ảnh hưởng các nước. Mặt phía trên của khối
granular body và granular base là các mặt thoáng.
Để thực hiện mô hình này, chúng tôi sử dụng và
phát triển bộ chương trình mở GDM_TK(2D) của
Viện nghiên cứu Cơ học và Xây dựng (LMGC),
Trường Đại học Montpllier, Pháp bằng ngôn ngữ
C++. Bước thời gian cài đặt trong mô hình tương
ứng là dt = 10
-5
(s), gia tốc trọng trường được lấy
bằng 9,81 (m/s
2
) cho toàn bộ 9 mô phỏng ở trên.
Trong bài toán này thì sự mất ổn định của đập là
khi mất sự liên kết giữa các phần tử với nhau
trong kết cấu dưới tác dụng của trọng lượng bản
thân của các phần tử, hệ số mái dốc, hệ số ma sát
giữa các phần tử.
4. KẾT QUẢ
4.1. Hình thái vận động của đập đá
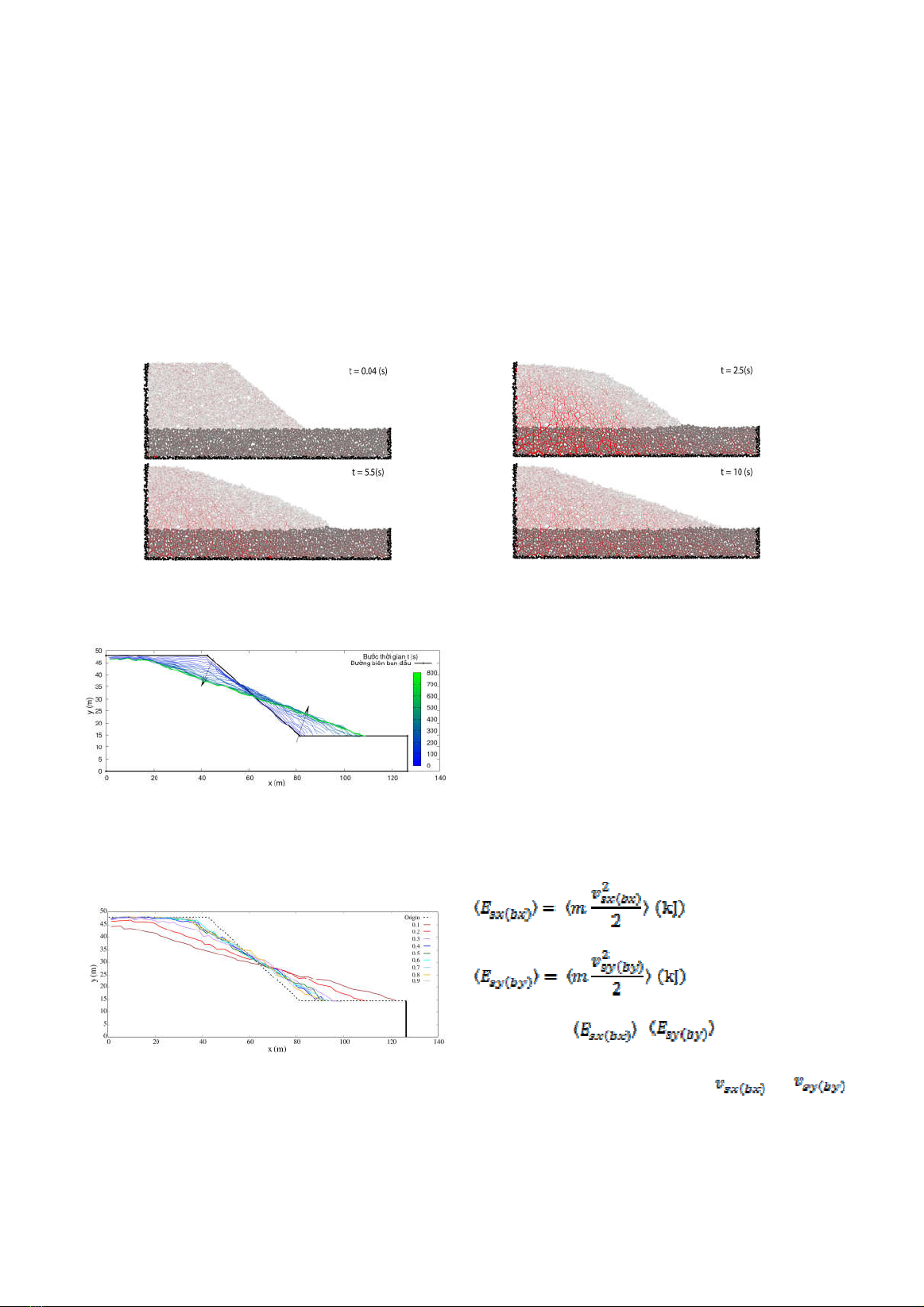
Hình 3 thể hiện sự thay đổi hình dạng của đập
đá theo bốn thời điểm khác nhau trong quá trình
mất ổn định của đập tương tứng với trường hợp hệ
số ma sát = 0,2. Có thể dễ dàng nhận thấy rằng,
đập đá đã có những biến dạng nhỏ tức thời ngay
sau khi kích hoạt sự mất ổn định của đập. Thân
đập đá bắt đầu dịch chuyển theo phương ngang,
quá trình dịch chuyển này dẫn đến chiều cao của
đập bị giảm. Đồng thời, dưới tác dụng của trọng
lượng và sự dịch chuyển của thân đập, phần chân
đập bắt đầu bị biến dạng, có xu hướng bị đẩy trồi
về phía trước chân đập. Thân và chân đập sau đó
đạt trạng thái ổn định ở giai đoạn cuối của quá
trình dịch chuyển. Hình 3 cũng giới thiệu hệ thống
lực tương tác giữa các phần tử đa giác với nhau
thuộc hai khối granular cũng như tương tác với
Cluster. Hệ thống lực được giới thiệu trên hình là
lực tương tác pháp tuyến, được nối từ tâm của các
phần tử khi có sự va chạm với nhau. Mật độ và độ
lớn của các lực này giảm dần từ chân đến đỉnh
đập. Đặc biệt, mật độ các lực rất bé ở bị trí chân
đập do sự vận động của thân đập theo phương
ngang. Những đặc điểm vận động và sự thay đổi
hình dạng của cả thân đập và chân đập rất có thể
sẽ bị chi phối bởi sự ma sát giữa các hạt vật liệu
cấu thành đập.
Hình 4 mô tả sự thay đổi mặt ngoài thân đập
trong suốt quá trình mất ổn định của đập đá.
Đường nét đứt được xác định tại tâm của các phần
tử. Chúng ta có thể thấy rằng các phần tử trên thân
đập bắt đầu dịch chuyển xuống theo hướng mũi
tên phía trên do ảnh hưởng của trọng lượng hạt vật
liệu, sau đó chảy dài về phía trước bên trên chân
đập, dẫn đến làm tăng phần thể tích đá ở phần này.
KHOA HỌC KỸ THUẬT THỦY LỢI VÀ MÔI TRƯỜNG - SỐ 86 (12/2023)
7
Trong quá trình dịch chuyển đó của thân đập, đã
tác động lên khối chân đập đá, gây nên hiện tượng
đẩy các phần tử của chân đập dịch chuyển theo.
Các phần tử thuộc 2 khối này dừng lại khi năng
lượng E (kJ) hay động năng giảm đến bằng không.
Chúng ta có thể thấy rõ sự khác biệt về mặt
thoáng ở trạng thái cân bằng cuối cùng khi thay
đổi hệ số ma sát từ 0,1 đến 0,9, như thể hiện ở
Hình 5. Việc gia tăng hệ số ma sát giữa các hạt vật
liệu đã làm giảm đáng kể sự vận động của thân
đập đá. Cụ thể, khi hệ số ma sát có giá trị nhỏ như
0,1; 0,2; 0,3 thì sự ảnh hưởng này rất lớn, trường
hợp hệ số lớn hơn ví dụ như từ 0,4 đến 0,9 thì sự
khác biệt này rất nhỏ. Điều này có thể hiểu là hệ
số ma sát đã ảnh hưởng lớn đến sự tương tác giữa
các phần tử với nhau, xuất hiện lực tiếp tuyến tại
tương tác có giá trị lớn hơn, nên đã giảm sự trượt,
lăn của các phần tử trong kết cấu. Hay nói cách
khác, gia tăng hệ số mat sát trượt giữa các hạt vật
liệu đã làm gia tăng sức khác trượt của thân đập,
dẫn đến đập đá ổn định hơn khi các phần tử đá sử
dụng có hệ số ma sát hay độ gồ ghề lớn.
(a) (b)
(c) (d)
Hình 3. Mô phỏng các trạng thái ở trường hợp
= 0,2 tại các mốc thời gian khác nhau.
Đường màu đỏ là hệ thống các mạng lưới lực tương tác giữa các phần tử.
Hình 4. Mô tả quá trình dịch chuyển của các
phần tử trong khối granular body của mô phỏng
khi hệ số ma sát là 0,2 qua hơn 800 bước mô
phỏng theo thời gian t (s).
Hình 5. Mô tả mặt thoáng ở trạng thái cuối cùng
của 9 mô hình mô phỏng
4.2. Năng lượng của các khối phần tử
Ngoài sự thay đổi hình dạng của đập đá trong
quá trình mất ổn định, tốc độ dịch chuyển của thân
đập và chân đập theo các phương khác nhau là
những đại lượng đặc trưng cho sự vận động của
đập. Như nghiên cứu của Yesheng Wu và các
cộng sự (Wu và nnk., 2018, và 2021), những tốc
độ dịch chuyển này được đặc trưng bởi động năng
trung bình của các hạt vật liệu trong hai phần:
phần thân và phần chân đập đá theo các phương x,
y khác nhau, như thể hiện ở phương trình (3), (4):
(3)
(4)
Trong đó , lần lượt là động
năng trung bình của các hạt vật liệu trong thân đập
(chân đập) theo phương x và y, và
(m/s) lần lượt là giá trị đại số của vận tốc của
phần tử trong thân đập (chân đập) tại thời điểm
tính toán.


























