Chapter 4: Properties of Regular
Languages
Quan Thanh Tho
qttho@cse.hcmut.edu.vn
Theorem 4.1
If L1 and L2 are regular, then so are L1∩L2,
L1∪L2 , L1L2 , L1, L1*.
(The family of regular languages is closed
under intersection, union, concatenation,
complement, and star-closure.)
Proof
•L1 = L(r1) L2 = L(r2)
L(r1 + r2) = L(r1)∪L(r2)
L(r1 . r2) = L(r1)L(r2)
L(r1*) = (L(r1))*
Proof (cont’d)
•M = (Q, Σ, δ, q0, F) accepts L1.
M = (Q, Σ, δ, q0, Q – F) accepts L1.
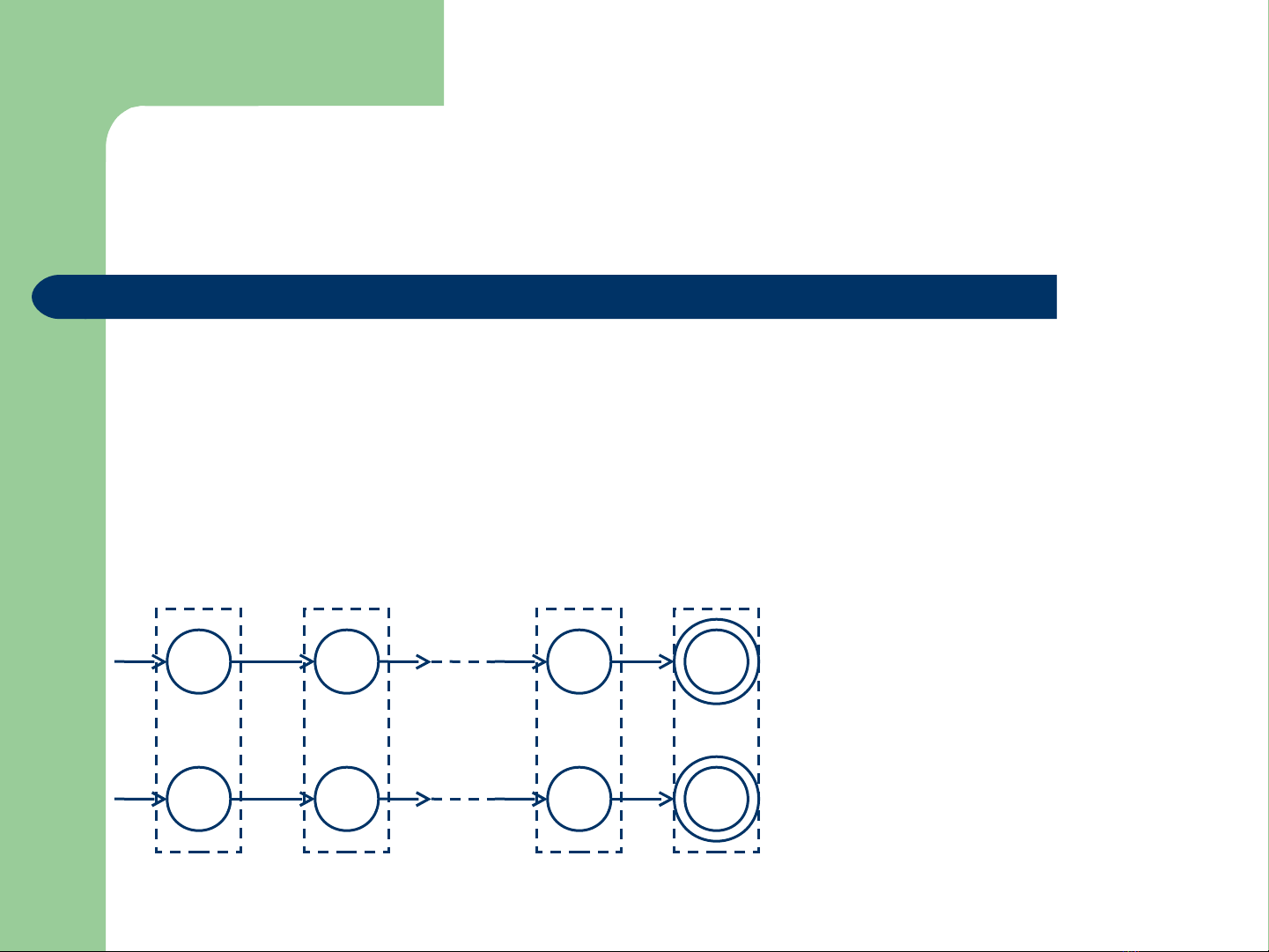
Proof (cont’d)
M1 = (Q, Σ, δ1, q0, F1) accepts L1.
M2 = (P, Σ, δ2, p0, F2) accepts L2.
q0qf
a1an
p0pf
a1anδ2(pj, a) = pl
δ1(qi, a) = qk
δ1((qi, pj), a) = (qk, pl)