BÀI 5: HÌNH BÌNH HÀNH – HÌNH CHỮ NHẬT
A. MỤC TIÊU:
* Củng cố và nâng cao kiến thức về hình bình hành và hình chữ nhật
* Vận dụng thành thạo kiến thức vào các bài tập về Hbh và hcn
* HS có hứng thú và nghiêm túc trong học tập
B. HOẠT ĐỘNG DẠY HỌC:
I. Nhắc lại kiến thức bài học:
Kiến
thức
Hình bình hành Hình chữ nhật
1. Định
nghĩa
ABCD là Hbh
AB // CD
AD // BC
ABCD là Hcn
0
A = B = C = D 90
2. Tính
chất
ABCD là Hbh , AC
BD = O ABCD l Hcn , AC
BD = O

AB = CD, AD = BC
A = C , B = D
OA = OC, OD = OB
AB = CD, AD = BC
A = C , B = D
OA = OC, OD = OB
AC = BD
3. Dấu
hiệu
nhận
biết
ABCD
là Hbh
II. Bài tập vận dụng:
Hoạt động của GV Hoạt động của HS
1. Bài 1:
Cho Hbh ABCD có
0
A = 120
. Đường phân
giác của góc D đi qua trung điểm của AB
a) C/m: AB = 2AD
b) Gọi F là trung điểm của CD.
HS ghi đề, vẽ hình
+
0
A = B = C = 90
+ ABCD có AB // CD
Và
0
A = D = 90
+ ABCD là Hbh có:
-
0
A = 90
- AC = BD
ABCD
Là hcn
AB // CD, AD // BC
AB = CD, AD = BC
A = B , C = D
OA = OC, OB = OD
( O = AC BD)
C/m
ADF đều,
AFC cân
c) C/m AC
AD
Giải
Gọi E là trung điểm của AB.
Ta có
ADE là tam giác gì? Vì sao?
Hãy C/m điều đó
Hãy C/m
ADF cân tại A có một góc
600
Hãy C/m
AFC cân tại F
F
E
DC
BA
a)
ADE là tam giác cân
Ta có
0
A = 120
, mà ABCD là Hbh nên
0
D = 60
0
ADE = AED = 30
ADE cân tại A
AD = AE mà AB = 2 AE
Nên AB = 2AD
b) AB = CD (do ABCD là Hbh)
mà DF =
1
2
CD, AD =
1
2
AB. Suy ra
AD = DF
ADF cân trại D có
0
D = 60
vậy:
ADF là tam giác đều
Ta có AF = DF (do
ADF đều)
Mà DF = FC (F là trung điểm của BC)
Suy ra AF = FC
AFC cân tại F
T
ừ
AFC cân t
ại F ta suy ra điều g
ì?
Góc DFA bằng hai lần góc nào của
AFC
DAC
=?
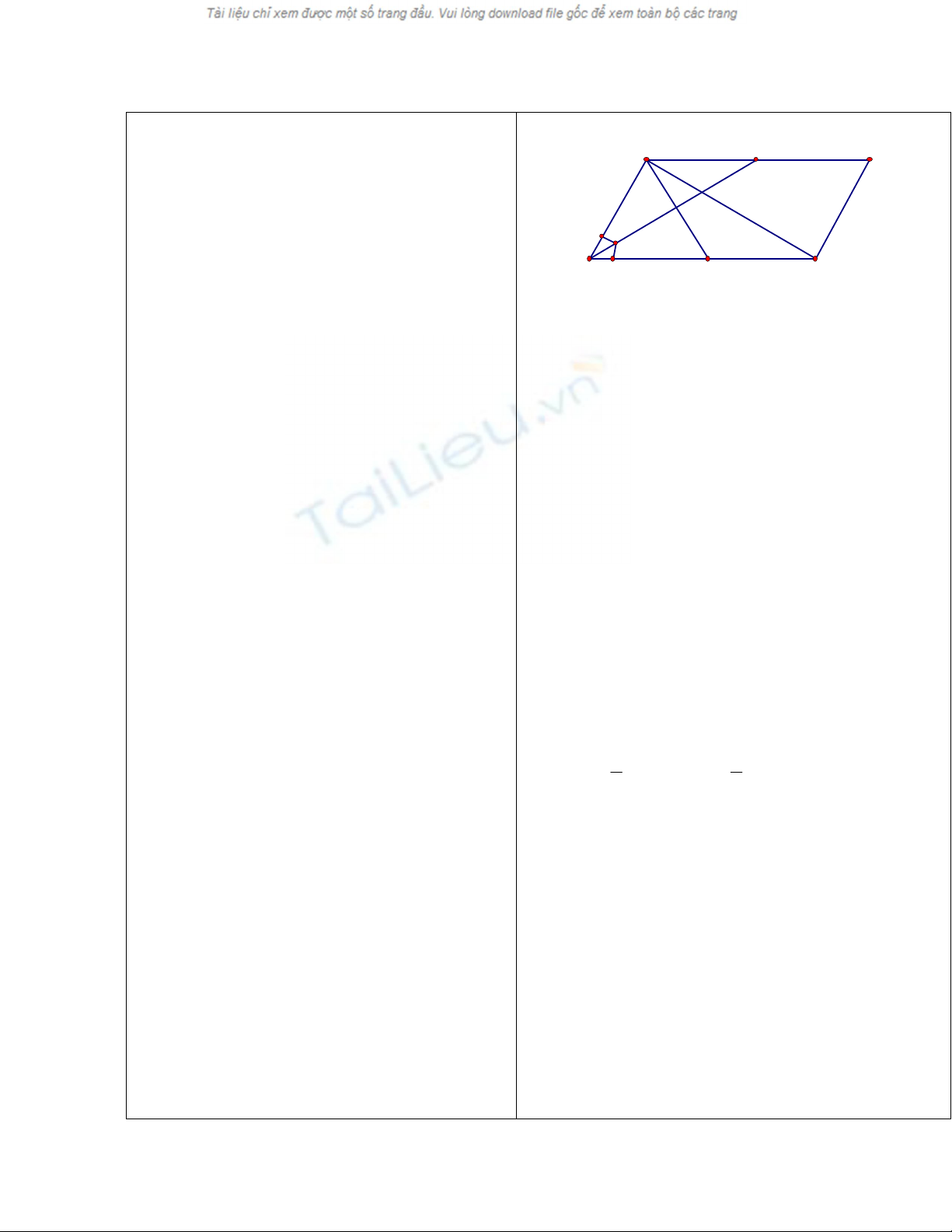
2. Bài 2:
Cho
ABC và O là điểm thuộc miền
trong của tam giác đó. Gọi D, E, F lần
lượt là trung điểm của AB, BC, CA và L,
M, N lần lượt là trung điểm của OA, OB,
OC
Chứng minh rằng các đoạn thẳng EL, FM,
DN đồng quy
Giải
Để C/m ba đoạn thẳng EL, FM, DN đồng
quy ta C/m gì?
Ta C/m các đoạn thẳng đó là đường chéo
của hai hbh có chung một đường chéo
Để C/m tứ giác EFLM là Hbh ta c/m như
thế nào?
Tương tự ta có tứ giác NLDE là hình gì?
c)
AFC cân tại F
DFA = 2FAC
(Góc ngoài
tại đỉnh của tam giác cân)
Mà
0
FDA = 60
(do
ADF đều). Suy ra
0
FAC = 30
0
DAC = 90
hay AC
AD
HS ghi đề, vẽ hình
L
MN
OF
E
D
C
B
A
HS suy nghĩ , phát biểu
HS ghi nhớ phương pháp c/m
E, F là trung điểm của BC, CA
EF là đường
trung bình của
ABC suy ra
EF // AB, EF =
1
2
AB (1)
Tương tự LM là đường trung bình của
OAB

Hai Hbh này có chung đư
ờng chéo n
ào?
Từ đó ta có kết luận gì?
Những Hbh nào có tâm trùng nhau?
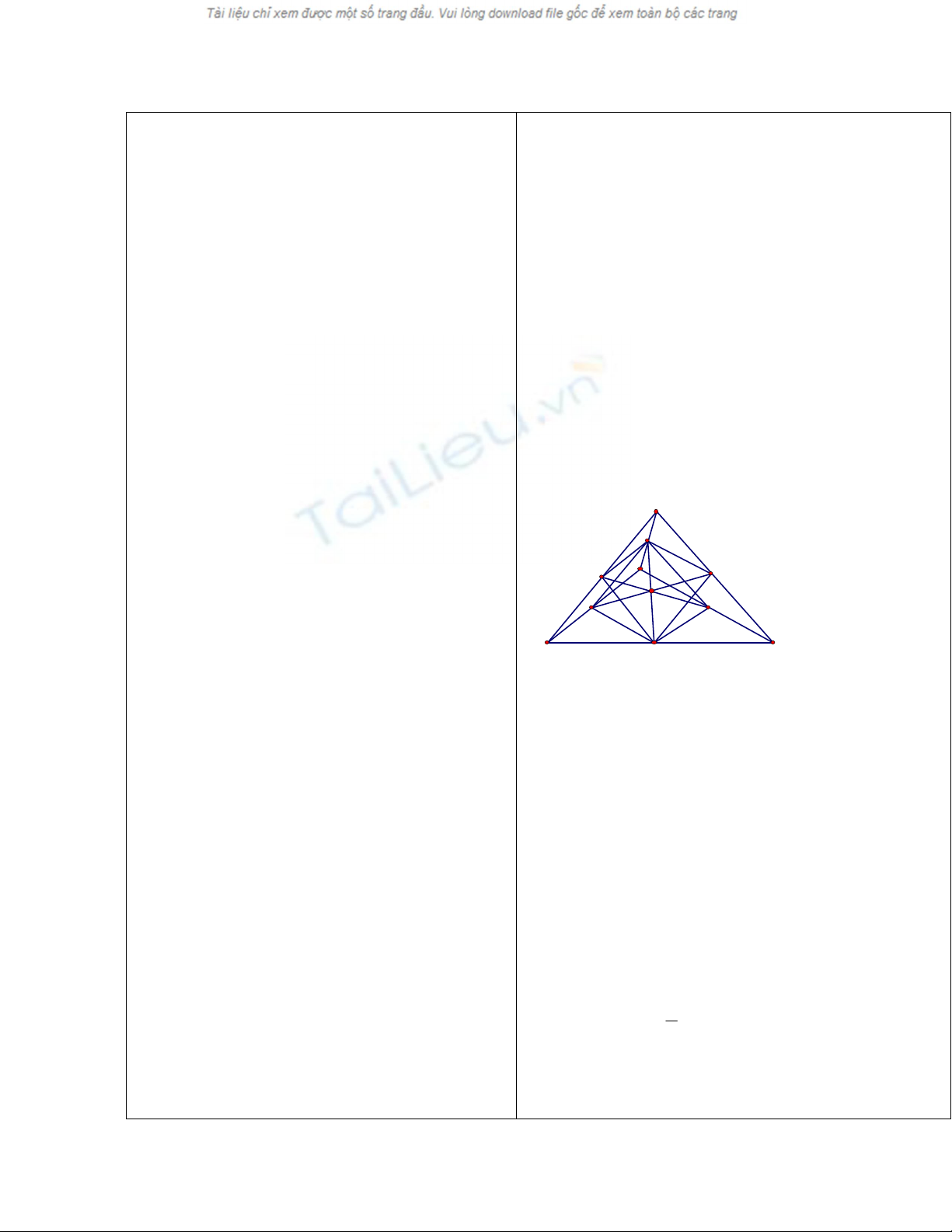
3. Bài 3:
Cho hìn chữ nhật ABCD; kẻ BH
AC.
Gọi E, F lần lượt là trung điểm của AH,
CD. Chứng minh BE
EF
Giải
Gọi K là trung điểm của AB ta có điều gì?
Vì sao?
suy ra LM // AB, LM =
1
2
AB (2)
Từ (1) và (2) suy ra tứ giác EFLM là Hbh
C/m tương tự ta có tứ giác NLDE là Hbh
(Vì có NE //= LD)
Hai Hbh EFLM và NLDE có chung đường
chéo LE hay ba đoạn thẳng EL, FM, DN đồng
quy tại trung điểm của LE
Hay ba Hbh EFLM , NFDM và NLDE có tâm
trùng nhau
HS ghi đề, vẽ hình
Gọi K là trung
điểm của AB ta có
EK // HB (Vì EK
là đường trung bình của
AHB) mà BH
AC
EK
AC suy ra
0
CEK = 90
CEK vuông tại E
K
I
F
E
H
DC
B
A
















