
CHƯƠNG 4
HỆ MẬT MÃ KHÓA CÔNG KHAI
(HỆ MẬT BẤT ĐỐI XỨNG)
10/ 10/ 2012 1ATBMTT_CHAP 4

4.1.1. Vấn đề sử dụng và phân phối khóa
Hệ mật bất đối xứng khắc phục được tính chất phức tạp
trong việc phân phối khóa ở hệ mật đối xứng
Cho phép giao tiếp giữa các đối tượng một cách uyển
chuyển , dễ dàng.
Sử dụng hai khoá Kp(public key ) và Ks(private key ) để
mã và giải mật
Có hai mode làm việc :
Bảo mật : M ã bằng public key giải mật bằng private key
Xác thực : M ã bằng private key giải mật bằng public key
10/ 10/ 2012 ATBMTT_CHAP 4 2
4.1. Khái niệm

4.1.2. Các yêu cầu của loại hệ mã PKC
- Việc sinh KP
, KS
phải dễ dàng
- Việc nh E(KP, M ) là dễ dàng
- Nếu có C = E(KP, M ) và KSthì dễ ràng giải mật .
- Nếu biết KP thì việc dò tìm KS
là khó
- Rất khó tìm bản rõ từ bản mã nếu không biết khóa .
10/ 10/ 2012 ATBMTT_CHAP 4 3
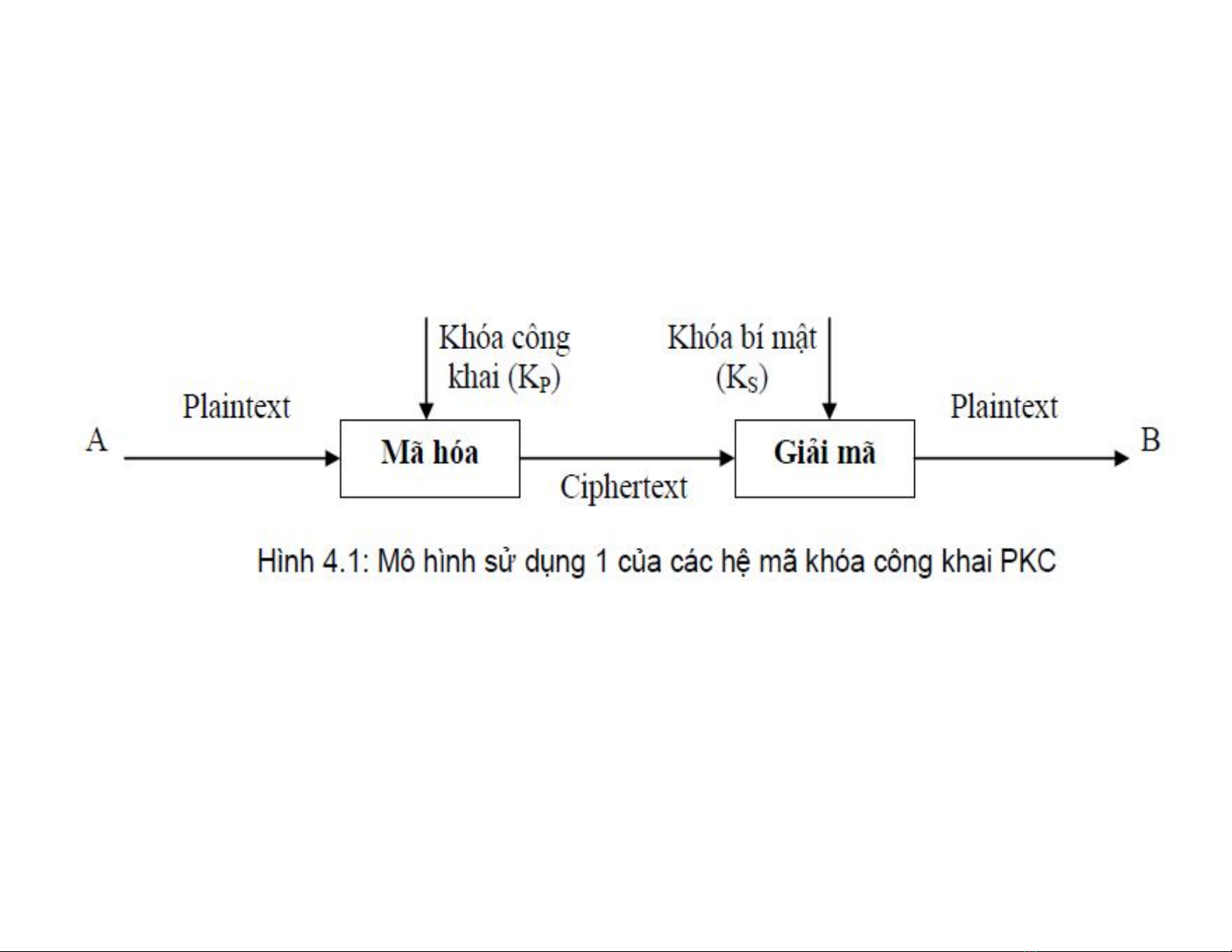
4.1.3. các mô hình sử dụng PKS
10/ 10/ 2012 ATBMTT_CHAP 4 4
4.1.3.1. M ô hình bảo mật
Ciphertext = E(KP
,P) , Plantext = D(KS
, E(KP
,P))
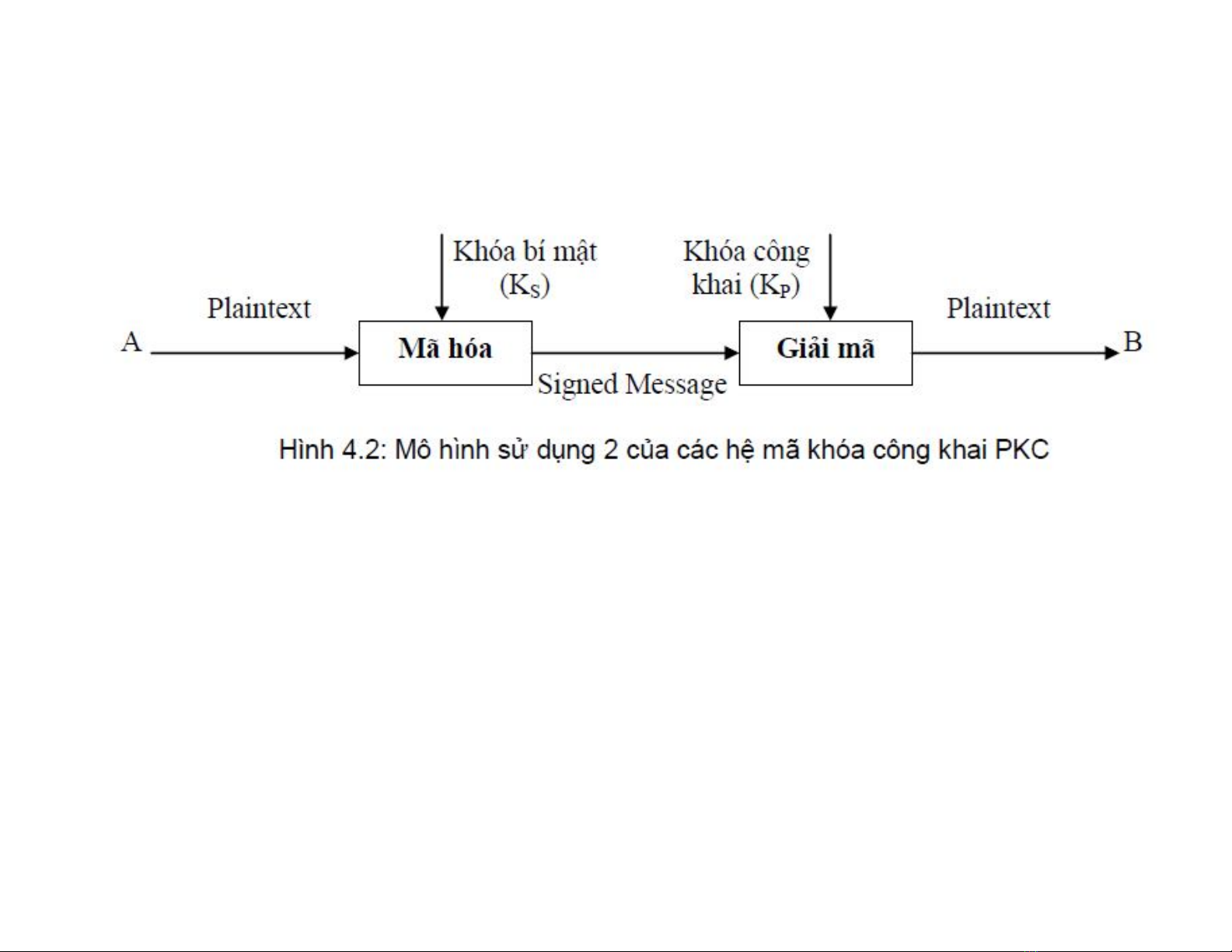
4.1.3.2.M ô hình xác thực
10/ 10/ 2012 ATBMTT_CHAP 4 5
Ciphertext = D(KS
, P) , Plaintext = E(KP
, D(KS
, P))


























