Bài giảng Chi tiết máy: Chương 3 - TS. Phạm Huy Hoàng

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:13

Thêm vào BST

Báo xấu

8
lượt xem 3
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng "Chi tiết máy: Chương 3 - Động lực học cơ cấu" được biên soạn với các nội dung chính sau đây: Phân lọai lực; Áp lực tại các khợp phẳng thường gặp; Nhóm tĩnh định/ Nhóm Axua; Giải bài toán lực bằng phương pháp phân tích lực;... Mời các bạn cùng tham khảo bài giảng!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Chi tiết máy: Chương 3 - TS. Phạm Huy Hoàng

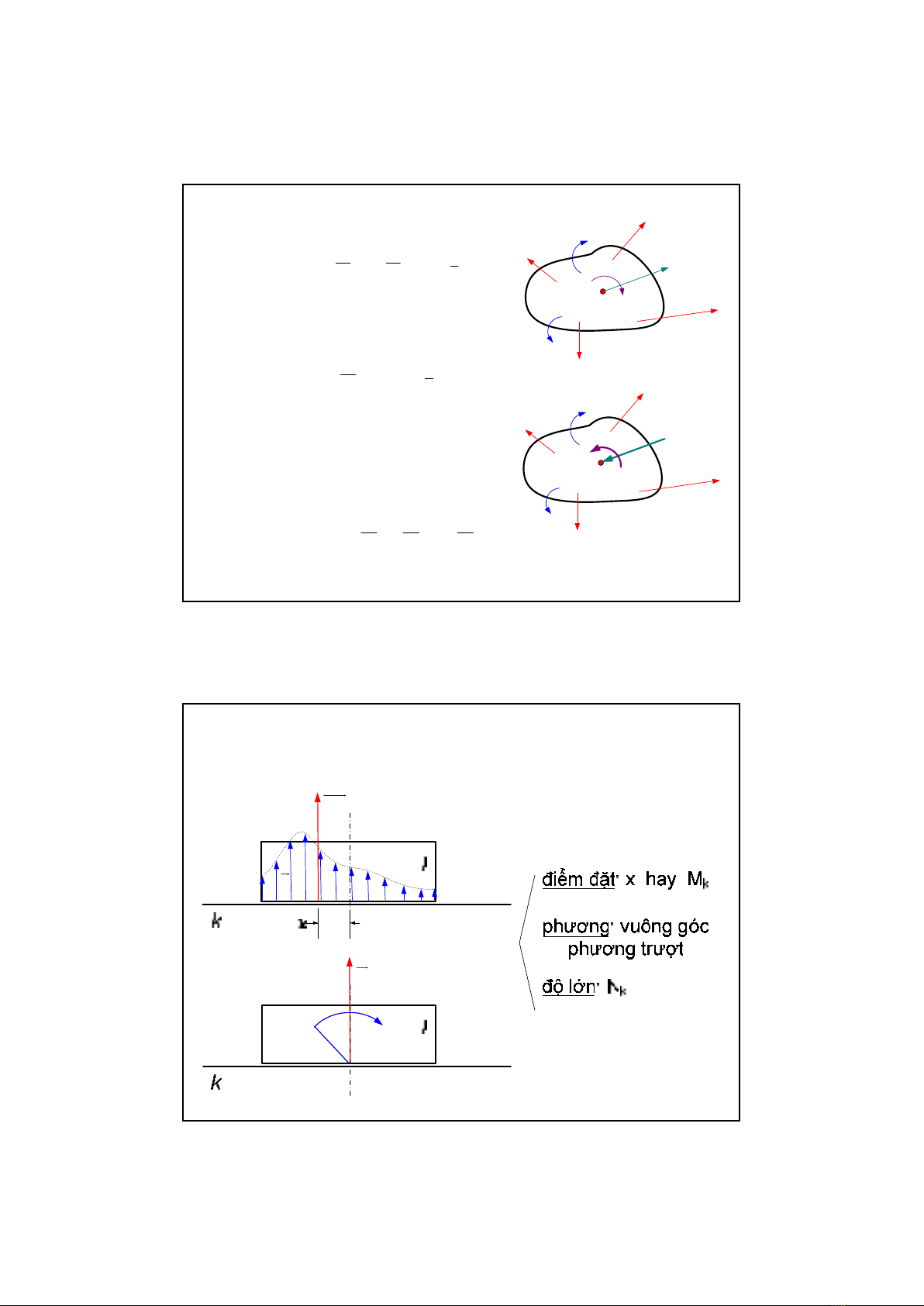
CHƯƠNG 3 ĐỘNG LỰC HỌC CƠ CẤU TS. PHẠM HUY HOÀNG Chương 3: Động lực học cơ cấu I. Mở đầu: 1. Phân lọai lực: a. Ngọai lực: Lực phát động; Lực cản kỹ thuật (lực cản có ích); Lực ma sát do môi trường; Trọng lực các khâu; Lực quán tính - Ngọai lực “giả”. b. Nội lực: Áp lực khớp động; Lực ma sát trong khớp. 1
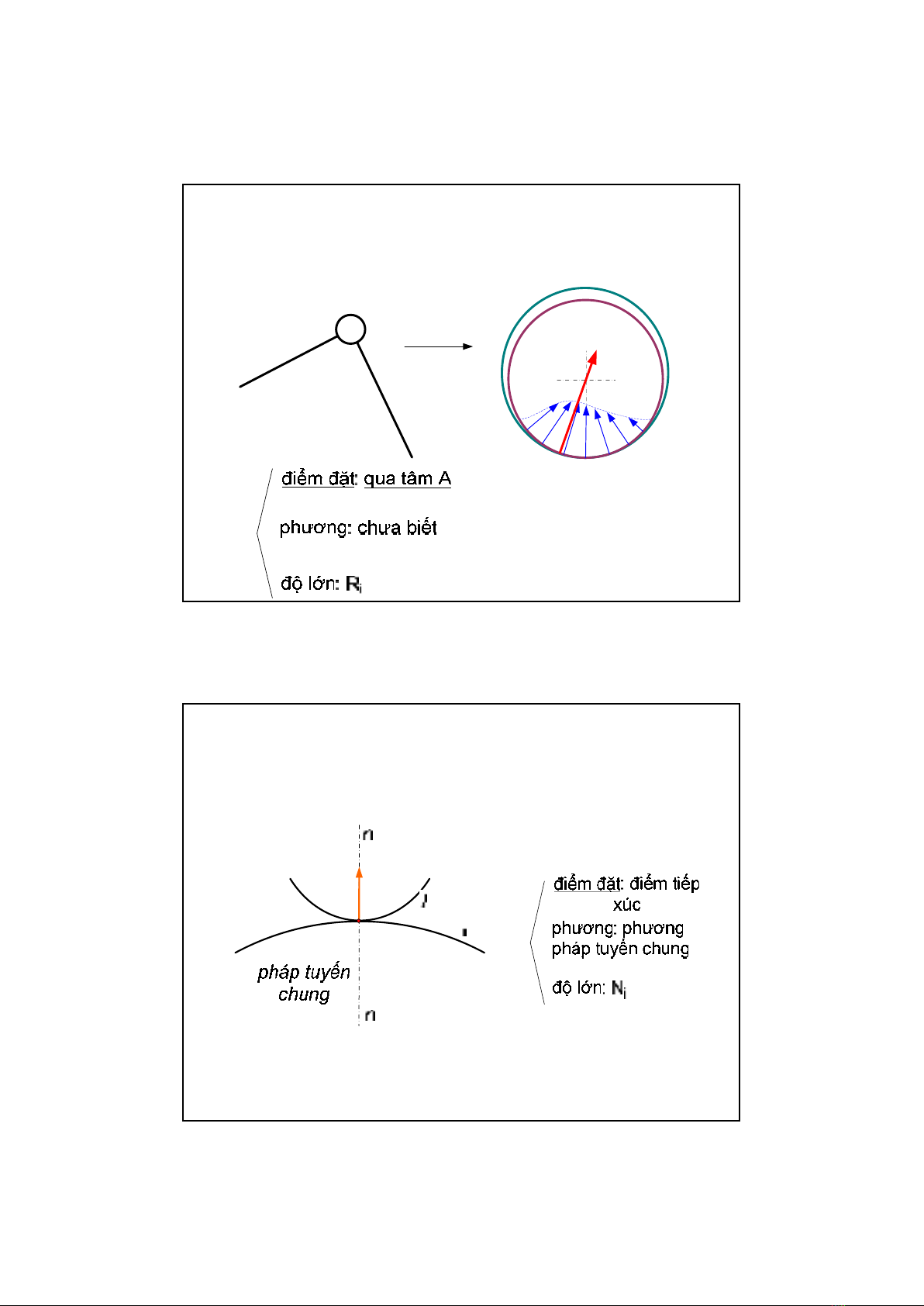
* Lực quán tính - Ngọai lực “giả”: r r M2 F2 F1 r r r r aSi å Fi = mi aSi ; å M i + å M F = J ie i i r i i i ei F3 Si i r M1 F4 Lực quán tính: r r Fqt = - mi aS ; M qt = - J ie i i i i r r M2 F2 F1 r Fqt i r M qt F3 Si i i r M1 F4 r r r å Fi + Fqti = 0; å M i + M F + M qti = 0 i i i 2. Áp lực tại các khợp phẳng thường gặp: a. Khớp tịnh tiến lọai 5: 2 ẩn số - độ lớn và điểm đặt N kj p r N kj = N kj M kj M kj = x.N kj 2
2. Áp lực tại các khợp phẳng thường gặp: b. Khớp bản lề: 2 ẩn số - độ lớn và phương lót ổ i A ngõng trục j r i Rij A j r p r Rij = 2. Áp lực tại các khợp phẳng thường gặp: c. Khớp lọai 4: 1 ẩn số - độ lớn áp lưc r Nij r Nij = 3
3. Nhóm tĩnh định / Nhóm Axua: Nhóm tĩnh định: có thể giải bài tóan lực - số ẩn bằng số phương trình Nhóm Axua: bậc tự do bằng 0 Xét nhóm các khâu phẳng có: n khâu động, p4 khớp lọai 4 và p5 khớp lọai 5 Bài toán lực: số phương trình 3n, số ẩn (p4+2 p5) Bậc tự do: 3n - (p4+2 p5) Điều kiện tĩnh định Ξ Điều kiện Axua: 3n - (p4+2 p5) = 0 3. Nhóm tĩnh định / Nhóm Axua: Nhóm phẳng toàn khớp thấp: n khâu động và p5 khớp lọai 5 Điều kiện tĩnh định Ξ Điều kiện Axua: 3n - 2 p5 = 0 → Nhóm {2 khâu 3 khớp}, {4 khâu 6 khớp}, {6 khâu 9 khớp}, 4
4. Giải bài toán lực bằng phương pháp phân tích lực: a. Giải các bài toán vị trí, vận tốc và gia tốc, để có số liệu về các lực quán tính trên mỗi khâu. b. Xác định các lực đã biết và chưa biết, xác định lực cân bằng ở dạng nào (lực hay moment) và tác động trên khâu nào. Lực cần bằng: ngọai lực chưa biết cân bằng tất cả các ngọai lực còn lại. c. Tách cơ cấu thành các nhóm tĩnh định và đặt các áp lực khớp động lên các thành phần khớp động có lưu ý tới sự bằng nhau về độ lớn và ngược chiều nhau cuả lực và phản lực tại các khớp (định luật III Newton). 4. Giải bài toán lực bằng phương pháp phân tích lực: d. Giải bài toán lực (tìm áp lực tại các khớp động) cho các nhóm theo thứ tự “từ xa về gần”: - Giải cho nhóm ở xa hơn (ở nhóm chứa các lực đã biết), lấy kết quả tìm được làm dữ liệu (coi như lực đã biết) của nhóm kế tiếp và gần hơn. - Công việc trên được lần lượt thực hiện cho tới khi chỉ còn lại khâu dẫn. e. Giải bài toán lực cho khâu dẫn (tính áp lực khớp động tại khớp nối khâu dẫn với giá và lực cân bằng). 5
5. Phương pháp công ảo / di chuyển khả dĩ: r Fi r r vi Fi Mi wi r Fqti r v Si M qt i N cb N cb = M cb .w1 M cb r r r r N cb = Pcb .v cb Pcb v cb ( ) n r r n r r N cb + å (Fi .vi + M i .wi ) + å Fqti .vSi + M qti .wi = 0 i =1 i =1 2 II. Ví dụ 1: D r F2 B 1 M qt 2 M1 r w1 F3 r C Fqt 3 A 0 3 3 3 l AB = a, l BC = a 3, l BD = a, lCD = a, ÐCAB = 60o 2 2 w 1 = w º const F2 = F3 = 3Fqt 2 = 3Fqt 3 = 3F M qt 2 = Fa r Rij = ?, M1 = ? 6
r r F2 R21 M qt 2 M1 r M1 r F3 w1 Fqt 3 r R01 r r r r R12 M F2 R12 F2 qt 2 r M qt 2 R32 r N 03 M 03 r r F3 r N 03 Fqt 3 M 03 r r F3 Fqt 3 r R23 r r R12 M F2 qt 2 r R32 r r r ìïF2 + R 12+ R32 = 0 í r r r ïîMqt2 + M B (F2 ) + M B (R 12) + M B (R32) = 0 ì x x ï- F2 + R12 - R32 = 0 (1) ïï y y Û í- R12 + R32 = 0 (2) ï ïM + Rx 3 a - R y 3 a = 0 (3) ïî qt2 32 2 32 2 7
r N 03 M 03 r r F3 Fqt 3 r R23 r r r r ìï F3 + Fqt 3 + R23 + N 03 = 0 í r r r r ïîM C ( F3 ) + M C ( Fqt 3 ) + M C ( R23 ) + M C ( N 03 ) + M 03 = 0 ì- F + F + R x = 0 ( 4 ) ï 3 qt 3 23 ï y Û í N 03 - R23 = 0 (5) ï ïM 03 = 0 ( 6) î r r R12 = - R21 : R12x = R21x , R12y = R21y r r R23 = - R32 : R23x = R32x , R23y = R32y r r r r R12 M F2 R12 F2 qt 2 r M qt 2 R32 r N 03 M 03 r r F3 r N 03 Fqt 3 M 03 r r F3 Fqt 3 ì R32x = R23x = F3 - Fqt 3 = 2 F r ï x ï R12 = R21 = 5F x R23 ï í 2( 3 + 1) ï N 03 = R23y = R32y = R12y = R21y = F ï 3 ïîM 03 = 0 8
r r ì R21 + R01 = 0 í r r r B îM A ( R21) + M A ( R01) + M1 = 0 R 21 ì x x ï R01 = R21 = 5F ï 1 ï y y 2( 3 + 1) M1 Û í R01 = R21 = F ï 3 ï 3 x 1 y A r ïîM1 = 2 aR21 + 2 aR21 R01 M1 = 17 3 + 2 Fa 6 r r r r r M1w1 + F2vD 2 + M qt 2w2 + ( Fqt 3 + F3 )vC 3 = 0 M1w1 - F2v D 2 - M qt 2w2 + ( Fqt 3 - F3 )vC 3 = 0 M1w1 = F2v D 2 + M qt 2w2 + ( - Fqt 3 + F3 )vC 3 3 w 2 17 3 + 2 M1w1 = 3 F aw1 + Fa 1 + ( - F + 3 F ) aw1 = Faw1 > 0 2 3 3 6 r v r D2 F2 w2 M qt 2 w1 M1 r r F3 Fqt 3 r v3 M1 = 17 3 + 2 Fa 6 9
III. Ví dụ 2: l AB = a, l AC = a 3, 1 2 r F3 D ÐCAB = 90o M1 w 1 = w º const A B M F2 = F3 = 3Fqt 2 = 3Fqt 3 = 3F qt 2 M qt 2 = Fa r Rij = ?, M1 = ? 3 M qt 3 0 M3 C 10
ì- N + R x = 0 (1) r r ï 32 12 ìï R12 + N32 = 0 ï y í r r Û í- R12 = 0 ( 2) ïîM qt 2 + M 32 + M B ( R12 ) + M B ( N32 ) = 0 ï ïM qt 2 - M 32 = 0 (3) î r N 32 M 32 M qt 2 r R12 r r r ì F3 + R03 + N 23 = 0 ï r r r íM C ( F3 ) + M C ( R03 ) + M C ( N 23 ) + r F3 ï M 3 + M qt 3 + M 23 = 0 î M 23 r N 23 M qt 3 ì- F cos 30o + N + R x = 0 ( 4) M3 ï 3 23 03 r ï R03 Û í- F3 sin 30o + R03 = 0 (5) y ï ï- F3 cos 30o CD + N 23BC - M 3 + M qt 3 + M 23 = 0 (6) î 11
r r r x = Rx , R y = R y F3 R12 = - R21 : R12 21 12 21 r r x = Nx ,N y = N y N 23 = - N32 : N 23 32 23 32 M qt 2 M 23 = M 32 r R12 ì x x 9 3 ï R12 = R 21 = N 32 = N 23 = 4 F ï M qt 3 ïR y = R y = 0 M3 ï 12 21 r ï x - 3 3 r R03 ïR í 03 = F3 F 4 ï ï R y = 1 F3 = 3 F M 23 ï 03 2 2 r r ï N 23 N 32 M 32 ï ïî M 23 = M 32 = M qt 2 = Fa M qt 2 r M qt 3 R12 M3 r R03 ì x x 9 3 ï R01 = R21 = 4 F r r ï ì R01 + R21 = 0 ï y y í r r Û í R01 = R21 = 0 îM A ( R21) + M A ( R01) + M1 = 0 ï ïM1 = R x AB cos 60o ïî 21 r R21 M1 M1 = 9 3 r Fa R01 8 12
r r M 1w1 + F3v D 3 + M qt 2w 2 + M qt 3w3 + M 3w3 = 0 M 1w1 + F3v D 3 cos 150 o + M qt 2w 2 + M qt 3w3 - M 3w3 = 0 M 1w1 = - F3v D 3 cos 150 o - M qt 2w 2 - M qt 3w3 + M 3w3 M 1w1 = - F3 (CD w3 ) cos 150 o - M qt 2w 2 - M qt 3w3 + M 3w3 w 3 w w w M 1w1 = - 3 F (3a 1 )( - ) - ( Fa ) 1 - ( 2 Fa ) 1 + (3 Fa ) 1 > 0 r 4 2 4 4 4 F3 r M1 vD3 w1 M qt 2 M1 = 9 3 Fa w2 =w3 8 M qt 3 M3 13