DepartmentofAppliedMechanics
CHAPTER Cơhọckỹthuật:ĐỘNGLỰCHỌC
EngineeringMechanics:KINETICS
Mộtsốnguyênlýcơ học
BộmônCơhọcứngdụng
DepartmentofAppliedMechanics
Cơhọckỹthuật
ĐỘNGLỰCHỌC
EngineeringMechanics
KINETICS
ĐỘNGLỰCHỌC:
MỘTSỐNGUYÊNLÝCƠHỌC
GV:NguyễnQuangHoàng
DepartmentofAppliedMechanics 3
Mộtsốnguyênlýcơ học– SomemechanicalPrinciples
CÁCKHÁINIỆM
1. Cơhệkhôngtựdo,liênkếtvàphânloạiliênkết
2. Dichuyểnảo–bậctựdo–tọađộsuyrộng
3. Côngảo–lựcsuyrộng–liênkếtlýtưởng
DepartmentofAppliedMechanics 4
Mộtsốnguyênlýcơhọc–SomemechanicalPrinciples
1.Cơhệkhôngtựdo,Liênkếtvàphânloạiliênkết
Cơhệkhôngtựdohaycòngọilàcơhệchịuliênkếtlàcơhệmàvịtrívàvậntốccủacácđiểmthuộchệbị
ràngbuộcbởimộtsốđiềukiệnvềhìnhhọcvàđộnghọc.
Liênkếtlànhữngđiềukiệnràngbuộcđặtlênchuyểnđộngcủacácđiểmvàcácvậtrắnthuộccơhệ.Các
ràngbuộcnàythườngđượcbiểudiễnbằngcácphươngtrìnhhoặcbấtphươngtrình.
C
v
r
A
BA
By
fr r
frr l
fre
22
1
22
2
3
() 0,
() 0,
0
=-=
=- -=
=⋅=

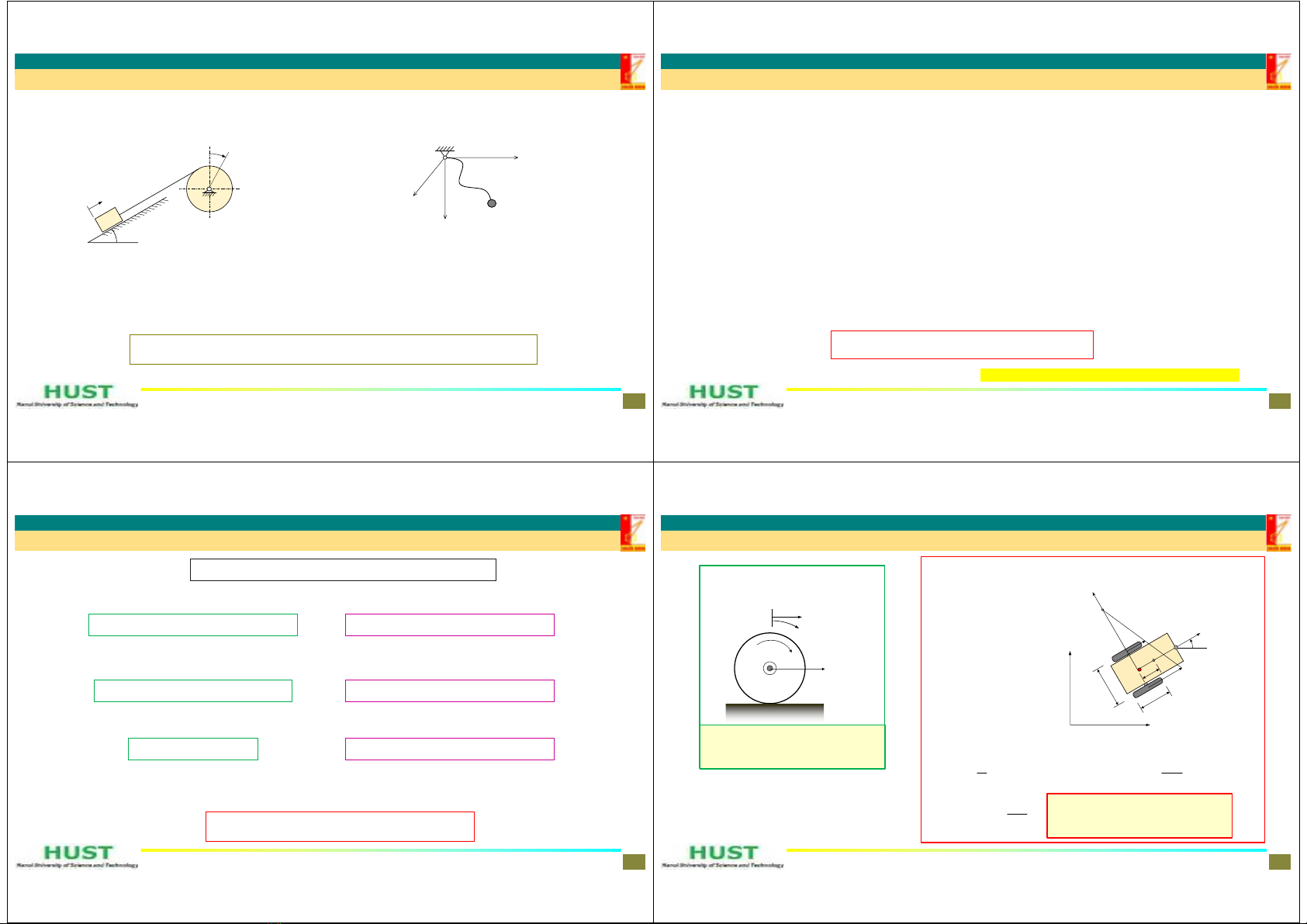
 10
f
vrw=- =
đốivớiđĩalănkhông
trượttrênnền
O
B
A
rl
x
,x
xe
,y
ye
DepartmentofAppliedMechanics 5
Mộtsốnguyênlýcơhọc–SomemechanicalPrinciples
1.Cơhệkhôngtựdo,Liênkếtvàphânloạiliênkết
s
O
rM
Ox
y
l
z
11
00fvr fsrwj=- = =- =
22
1() 0
M
fl r=- ³
đốivớihệtờikéo,khidâykhôngdãn dâytreokhôngdãn,cóthểtrùng
Viếtmộtcáchtổngquát,phươngtrìnhliênkếtđượcviếtdạngnhưsau:
11
( ,.., ,.., , ,.., ,.., , ) 0, 1,2,...,
j
kN k N
f
rrrvv vt j r³=


DepartmentofAppliedMechanics 6
Mộtsốnguyênlýcơ học– SomemechanicalPrinciples
1.Cơhệkhôngtựdo,Liênkếtvàphânloạiliênkết
Dựa vào phương trình hay bất phương trình liên kết phân các loại liên kết như sau:
Liên kết giữ và liên kết không giữ [hay còn gọi là liên kết hai phía và liên kết một phía]. Nếu các ràng buộc
được biểu diễn bằng phương trình thì đó là liên kết giữ. Trái lại, nếu ràng buộc được biểu diễn bằng bất
phương trình thì đó là liên kết không giữ.
Liênkếtdừngvàliênkếtkhôngdừng. Nếu trong phương trình liên kết không chứa tường minh biến thời
gian t, thì đó là liên kết dừng. Ngược lại, ta có liên kết không dừng.
Liênkếthôlônômvàliênkếtkhônghôlônôm.Nếu trong phương trình liên kết không chứa biến vận tốc
hoặc nếu có nhưng có thể tích phân để loại bỏ biến vận tốc thì đó là liên kết hô lô nôm (hay liên kết hình
học). Trái lại, nếu trong phương trình liên kết có chứa biến vận tốc mà ta không thể loại bỏ được thì đó là
liên kết không hô lô nôm (hay còn gọi là liên kết động học).
Trong phạm vi giáo trình chúng ta chỉ xem xét các cơ hệ chịu liên kết hô lô nôm và dừng.
1
( ,.., ,.., ) 0, 1,2,...,
j
kN
f
rrr j r==

Liênkếthôlônômlàliênkếtgiữvàkhôngchứabiếnvậntốc.
DepartmentofAppliedMechanics 7
Mộtsốnguyênlýcơhọc–SomemechanicalPrinciples
1.Cơhệkhôngtựdo,Liênkếtvàphânloạiliênkết
Liênkếtgiữvàliênkếtkhônggiữ
Liênkếtdừngvàliênkếtkhôngdừng
Liênkếthôlônômvàliênkếtkhônghôlônôm.
11
( ,.., ,.., , ,.., ,.., , ) 0, 1,2,...,
jkN kN
fr r r v v v t j r³=


11
( ,.., ,.., , ,.., ,.., , ) 0,
jkN kN
fr r r v v v t=


11
( ,.., ,.., , ,.., ,.., , ) 0,
jkN kN
fr r r v v v t³


11
( ,.., ,.., , ,.., ,.., ) 0,
jkN kN
fr r r v v v ³


11
( ,.., ,.., , ,.., ,.., , ) 0,
jkN kN
fr r r v v v t³


1
( ,.., ,.., , ) 0,
jkN
fr r r t=

11
( ,.., ,.., , ,.., ,.., , ) 0,
jkN kN
fr r r v v v t³


1
( ,.., ,.., ) 0, 1,2,...,
j
kN
f
rrr j r==

Liênkếthôlônômvàdừng
DepartmentofAppliedMechanics 8
Mộtsốnguyênlýcơ học– SomemechanicalPrinciples
1.Cơhệkhôngtựdo,Liênkếtvàphânloạiliênkết
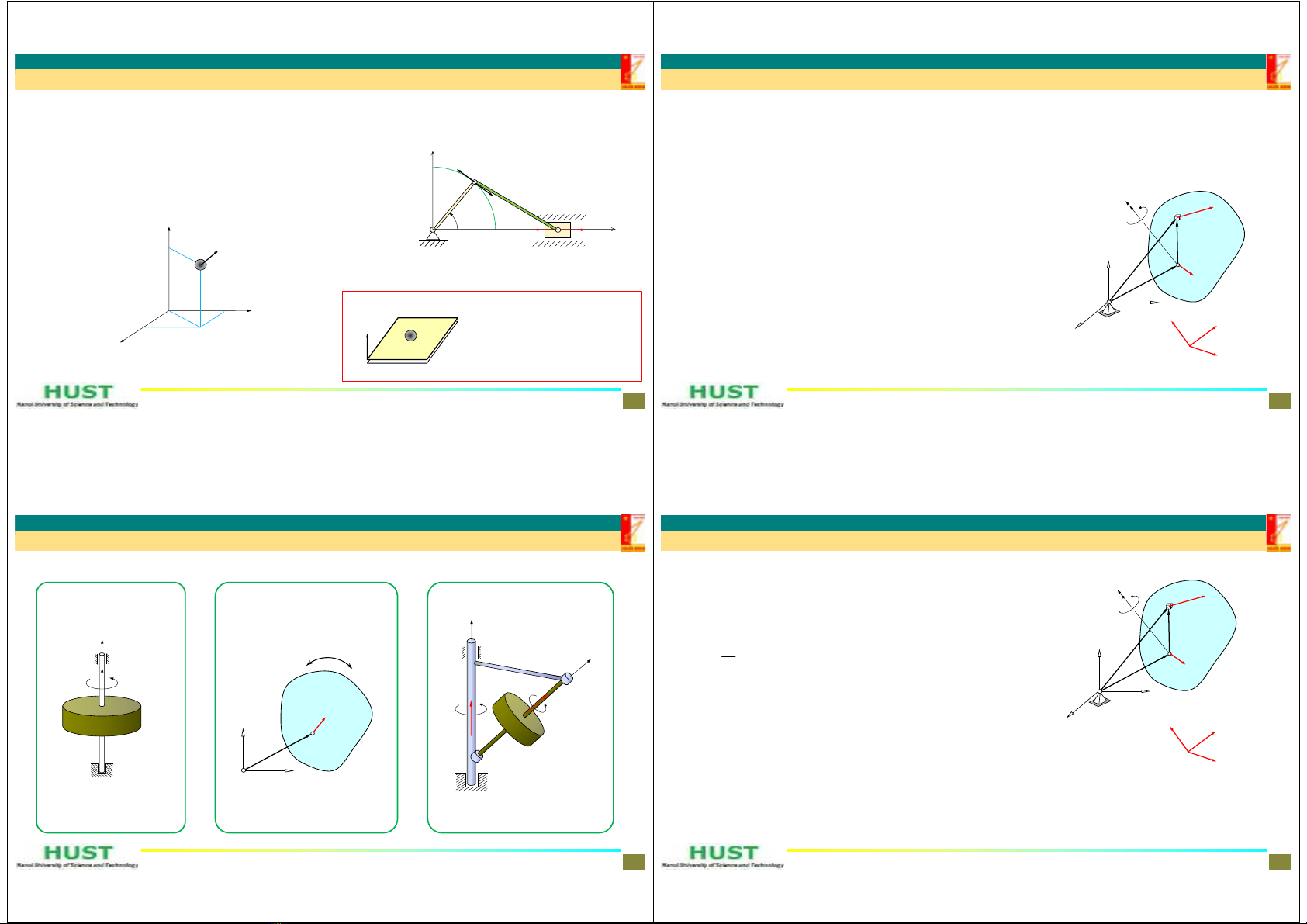
Vídụvềliênkếthôlônôm
x0
y0
O0
2L
2r
Ob
xb
ybP
vR
vL
C
d
O
vr srwj==
Vídụvềliênkếtkhônghôlônôm
11
(), ()
22
ORLb RL
vvvx vv
L
wy=+ == -

tan sin cos 0
O
OO
O
yxy
x
yyy= - =

v
x
DepartmentofAppliedMechanics 9
Mộtsốnguyênlýcơ học– SomemechanicalPrinciples
2.Dichuyểnảo– bậctựdo– tọađộsuyrộng
Dichuyểnảocủachấtđiểm
Dichuyểnảocủađiểmlàdichuyểnvôcùngbétưởngtượngtừvịtríđangxétsangcácvịtrílâncậnvàphù
hợpvớiliênkếttạithờiđiểmđangxét.
Lưuý:cácđặcđiểmcủadichuyểnảolà
1. vôcùngbé,
2. tưởngtượng,và
3. phùhợpliênkếttạithờiđiểmkhảosát.
A
O
B
x
y
A
rd
B
rd
xyz
rxe ye zedd d d=++

v
M
Sàn chuyển động, điểm M trên
mặt sàn. Khi xét di chuyển ảo
của điểm M, ta coi “thời gian
nhưdừnglại”(coisànnhưdừng
lại).
rd
,x
xe
,y
ye
,z
ze
DepartmentofAppliedMechanics 10
Mộtsốnguyênlýcơhọc–SomemechanicalPrinciples
2.Dichuyểnảo–bậctựdo–tọađộsuyrộng
Dichuyểnảocủavậtrắn
Di chuyển ảo của vật rắn là những di chuyển vô cùng bé tưởng tượng của vật rắn từ vị trí đang xét sang
các vị trí lân cận và phù hợp với liên kết tại thời điểm đang xét.
1
e
3
e
2
e
A
rd
A
P
O’
P
rd
w
r
A
r
u
A
rd
dj
Dichuyểnảocủavậtrắnbaogồmdichuyểnảocủa
điểmcựcAvàdichuyểnquayảoquanhtrụcnàođóqua
điểmcựcA:(trụcchứavéctơvậntốcgóc?)
,
A
rddj

Trongmộthệtrụctọađộcócơsở 123
[,, ]
T
eee=e

T
AA A A A
T
xyz
rxeyeze
eee
123
12
dd d d d
dj dj dj dj d
=++=
=++=
er
e


DepartmentofAppliedMechanics 11
Mộtsốnguyênlýcơ học– SomemechanicalPrinciples
2.Dichuyểnảo–bậctựdo–tọađộsuyrộng
Vídụ
Vậtrắnquayquanh
trụccốđịnh
z
e
dq
z
edj dq=

Vậtrắnquayquanh2
trụcgiaonhau
0zz
eedj dq db=+

db
0z
e
z
e
dq
z0
z
A
rd
A
O
A
r
A
rd
dj
Vậtrắnchuyểnđộng
phẳng
,
A
rddj
DepartmentofAppliedMechanics 12
Mộtsốnguyênlýcơ học– SomemechanicalPrinciples
2.Dichuyểnảo– bậctựdo– tọađộsuyrộng
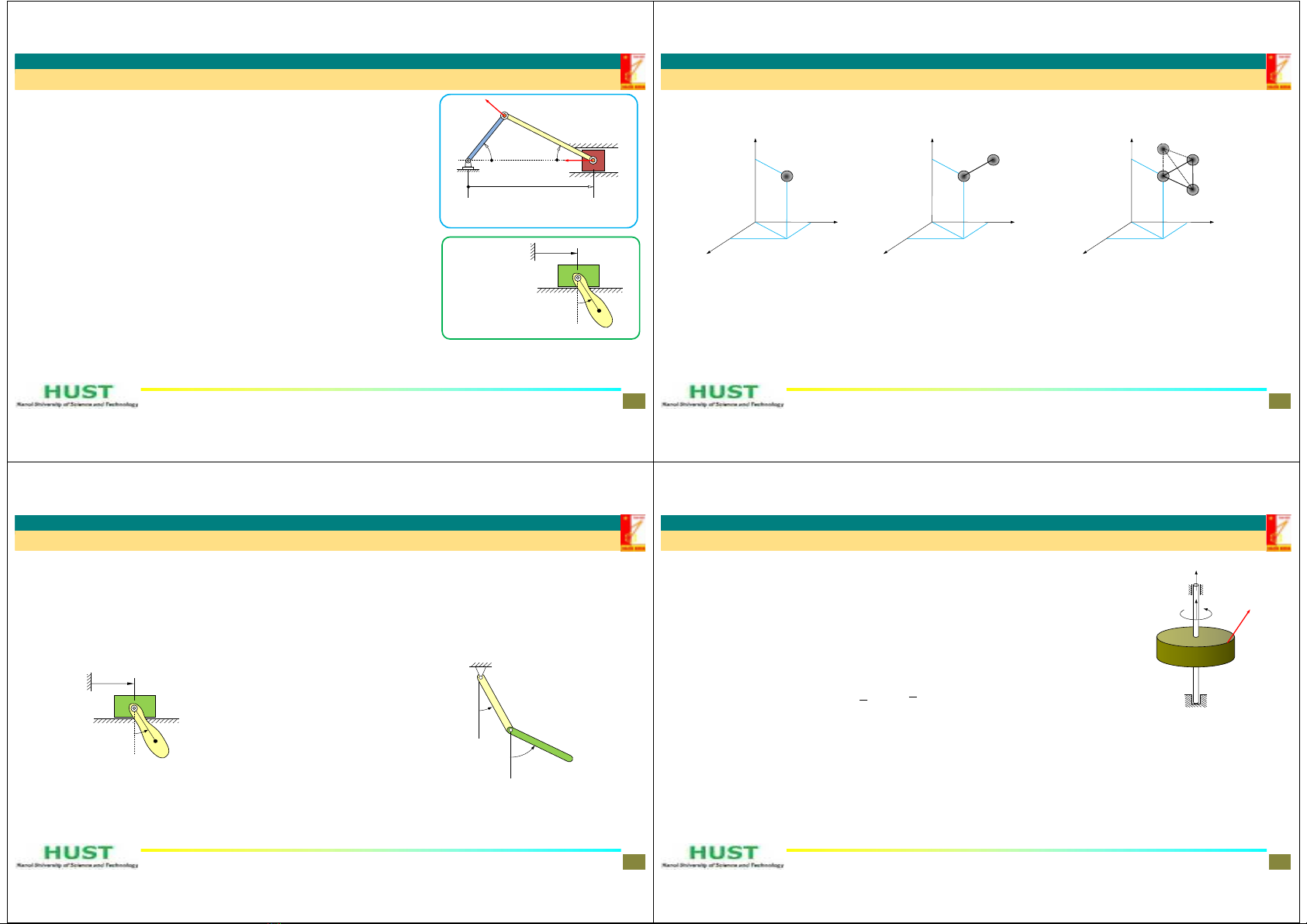
Dichuyểnảocủađiểmthuộcvậtrắn
1
e
3
e
2
e
A
rd
A
P
O’
P
rd
w
r
A
r
u
A
rd
dj
Trongmộthệtrụctọađộcócơsở 123
[,, ]
T
eee=e

,
T
PA P PPA
rr u rdddj d dddd=+´= =+er r r u

j
DichuyểnảocủađiểmPbấtkỳthuộcvật
PA P A
rru r r uddd=+ = +

du u du dt u du d u
dt ww j=´ = ´ = ´


PA A
uu
rrur u
ddj
dddddj
=´
=+=+´


DepartmentofAppliedMechanics 13
Mộtsốnguyênlýcơhọc–SomemechanicalPrinciples
2.Dichuyểnảo–bậctựdo–tọađộsuyrộng
Dichuyểnảocủacơhệ(Nchấtđiểmpvậtrắn)
Đối với cơ hệ tự do: tập các di chuyển ảo trên là độc lập tuyến tính.
Còn đối với cơ hệ không tự do (chịu liên kết): tập các di chuyển ảo
trên là không độc lập tuyến tính.
(
)
1
12 1
, ,..., , , ,..., ,
p
nA A p
rr r r rdd d d dj d dj

Di chuyển ảo của cơ hệ là tập các di chuyển ảo của các chất điểm và
các vật rắn thuộc hệ từ vị trí đang xét sang các vị trí lân cận và phù
hợp với liên kết tại thời điểm đang xét.
Bậctựdocủacơhệ
Bậc tự do của cơ hệ là số tối đa các di chuyển ảo độc lập.
Ví dụ một điểm tự do trong không gian 3D có ba bậc tự do vì nó
có thể di chuyển được tùy ý trong không gian. Khi có ràng buộc
đặt lên điểm này số bậc tự do của nó giảm. f=bậctựdocủacơhệ
s
C
A
(
)
,sddj
2f=
O
B
A
x
A
rd
B
rd
(
)
,,,
AB
rrdddjdq
 1f=
DepartmentofAppliedMechanics 14
Mộtsốnguyênlýcơ học– SomemechanicalPrinciples
2.Dichuyểnảo– bậctựdo– tọađộsuyrộng
Bậctựdocủacơhệ
HệNchấtđiểm,khoảngcáchgiữahaichấtđiểmkhôngđổi.
1
3
N
f
=
=
2, 1
5
Nr
f
==
=
3, 3
6
Nr
f
==
=
3, 3( 2) : 3 3( 2) 6NrN fNN³=- =--=
Vật rắn tự do trong không gian có bậc tự do 6f=
DepartmentofAppliedMechanics 15
Mộtsốnguyênlýcơhọc–SomemechanicalPrinciples
2.Dichuyểnảo–bậctựdo–tọađộsuyrộng
Tọađộsuyrộng
Tọa độ suy rộng là bộ các thông số đủ để xác định vị trí của cơ hệ, khi biết bộ thông số này vị trí của hệ
hoàn toàn được xác định. Các tọa độ suy rộng thường được ký hiệu bởi véc tơ
s
C
A
O
A
B
12
[ , ,..., ]
T
m
qq q=qTọa độ suy rộng đủ: m = f
Tọa độ suy rộng dư: m > f
2
2: [ , ]
4: [, , , ]
T
T
CC
f
ms
msxy
j
j
=
==
==
q
q
2
2: [ , ]
4: [ , , , ]
T
T
AABB
f
m
mxyxy
jq
=
==
==
q
q
DepartmentofAppliedMechanics 16
Mộtsốnguyênlýcơhọc–SomemechanicalPrinciples
3.Côngảo–liênkếtlýtưởng–lựcsuyrộng
Công ảo là công của lực khi điểm đặt của nó thực hiện di chuyển ảo.
xyz
AFr FxFyFzddddd=⋅ = + +
Công ảo của ngẫu lực tác dụng lên vật rắn
xx yy zz
Am m m mddjdjdjdj=⋅ = + +

Côngảocủalựctácdụnglênvậtrắnquayquanhtrụccốđịnh
()
z
AFr mFdd dq=⋅ = ⋅

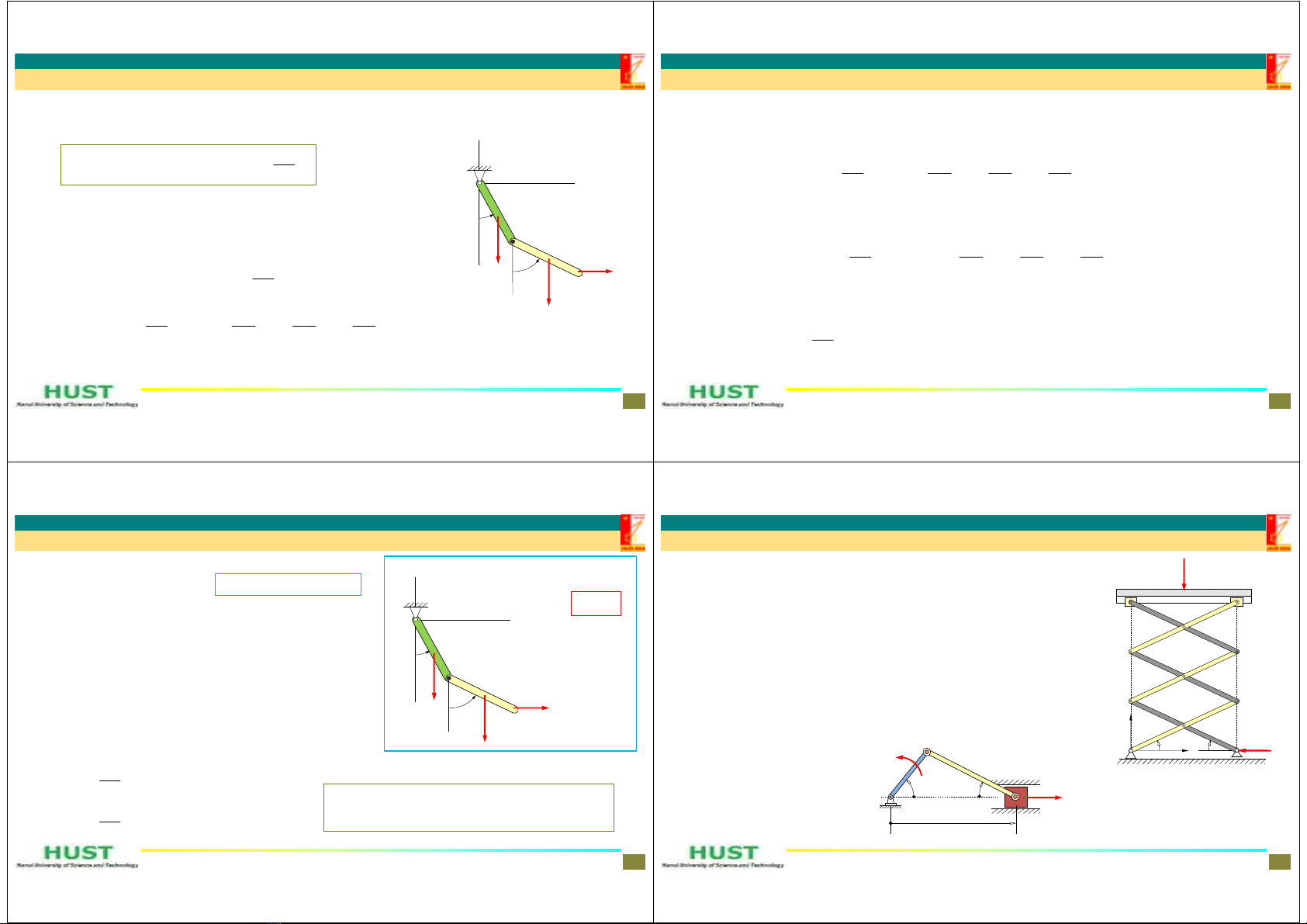
Liênkếtlýtưởng
Liên kết giữ được gọi là lý tưởng nếu tổng công ảo của các lực
liên kết trong mọi di chuyển ảo của cơ hệ đều bằng không:
1
0,
N
cc
kk k
k
AFr Fdd
=
=⋅=
å
cáclựcliênkết
e
dq
F
DepartmentofAppliedMechanics 17
Mộtsốnguyênlýcơ học– SomemechanicalPrinciples
3.Côngảo–liênkếtlýtưởng–lựcsuyrộng
Lựcsuyrộng
Gọi là tọa độ suy rộng đủ của cơ hệ chịu liên kết hôlônôm và dừng. Như thế vị trí một
điểm bất kỳ thuộc hệ sẽ là hàm của tọa độ suy rộng:
Tổngcôngảocủacáclựchoạtđộngtrongcácdichuyểnảo
12
[ , ,..., ]
T
n
qq q=q
12
1
( , ,..., )
n
k
kk n k i
ii
r
rrqq q r q
q
dd
=
==
å

111 1
NnN n
k
kk k i ii
kik k
i
r
AFr F q Qq
q
dd dd
=== =
æö
÷
ç÷
=⋅= ⋅ =
ç÷
ç÷
ç
èø
ååå å

11
, 1,2,...,
NN
kkkk
i k kx ky kz
kk
iiii
rxyz
QF F F F i n
qqqq
==
æö
¶¶
÷
ç÷
=⋅= + + =
ç÷
ç÷
ç
¶¶
èø
åå
làlựcsuyrộngcủacáclựchoạtđộngứngvớitọađộsuyrộngqi.
O
A
B
x
y
a1
l1
a2l2F
2
P
1
P
12 1 2
12 1 2
sin sin cos cos
cos cos sin sin
BB
BB
xl l xl l
yl l yl l
jqd jdj qdq
jqd jdjqdq
=+ = +
=- - = +
DepartmentofAppliedMechanics 18
Mộtsốnguyênlýcơ học– SomemechanicalPrinciples
3.Côngảo–liênkếtlýtưởng–lựcsuyrộng
Cáchtínhlựcsuyrộng
1.Tínhtheocôngthức
0, 0, ( )
ij
qq jidd¹="¹
12
, ( , ,..., )
ct
in
i
Qqqq
q
¶P
=- P=P
11
, 1,2,...,
NN
kkkk
i k kx ky kz
kk
iiii
rxyz
QF F F F i n
qqqq
==
æö
¶¶
÷
ç÷
=⋅= + + =
ç÷
ç÷
ç
¶¶
èø
åå
2. Cho hệ thực hiện di chuyển ảo đặc biệt
11
NN
kkkk
k i kx ky kz i i i
kk
iiii
rxyz
AF q F F F qQq
qqqq
dd dd
==
æö æ ö
¶¶
÷÷
çç
÷÷
=⋅ = + + =
çç
÷÷
çç
÷÷
çç
¶¶
èø è ø
åå
3. Lực suy rộng của các lực có thế
DepartmentofAppliedMechanics 19
Mộtsốnguyênlýcơhọc–SomemechanicalPrinciples
3.Côngảo–liênkếtlýtưởng–lựcsuyrộng
Vídụ:tínhlựcsuyrộng
12 1 2
12
12
sin sin cos cos
() ( cos) ( cos)
(cos), (cos)
BB
B
kt kt
xl l xl l
A F F x Fl Fl
QFl QFl
jq
jqd jdjqdq
dd jdj qdq
jq
=+= +
== +
==
11 2 1 2
11 21 22
11 21
22
cos ( cos cos )
()coscos
()sin
sin
ct
ct
mga mgl a
ma ml g mag
Qmamlg
Qmag
j
q
jjq
jq
j
j
q
q
P=- - +
=- + -
¶P
=- =- +
¶P
=- =-
11121
222
cos ( ) sin
cos sin
kt ct
kt ct
QQQ Fl mamlg
QQ Q Fl mag
jj j
qq q
jj
qq
=+= - +
=+= -
O
A
B
x
y
a1
l1
a2l2
2
P
1
P
xx
FFe=
12
2, ,
f
qqjq===
?,QQ
jq
Tínhlựcsuyrộngkhôngthế
Tínhlựcsuyrộngcóthế
() BB
AF F r F xddd=⋅ =

DepartmentofAppliedMechanics 20
Mộtsốnguyênlýcơhọc–SomemechanicalPrinciples
NGUYÊNLÝCÔNGẢO
1. Kháiniệmcơ hệcânbằng
2. Nguyênlýcôngảo
3. PTcânbằngchohệchịuliênkếtởdạng
tọađộsuyrộngđủ
4. Vídụápdụng
P
Q
O
AB
C
D
x
y
K
O
B
A
rl
x