Tröôøng Ñaïi Hoïc Coâng Nghieäp TP.HCM Khoa coâng ngheä ñieän töû
Chöông 6: Traûi phoå Th.S Lyù Tuù Nga
85
CHƢƠNG 2 TẠO MÃ TRẢI PHỔ
2.2 CÁC CHUỖI PN
Các tín hiệu trải phổ băng rộng tựa tạp âm đƣợc tạo ra bằng cách sử dụng các chuỗi mã
giả tạp âm (PN: Pseudo-Noise) hay giả ngẫu nhiên. Loại quan trọng nhất của các chuỗi ngẫu
nhiên là các chuỗi thanh ghi dịch cơ số hai độ dài cực đại hay các chuỗi m. Các chuỗi cơ số hai m
đƣợc tạo ra bằng cách sử dụng thanh ghi dịch có mạch hồi tiếp tuyến tính (LFSR: Linear
Feedback Shift Register) và các mạch cổng hoặc loại trừ (XOR). Một chuỗi thanh ghi hồi tiếp
dịch tuyến tính đƣợc xác định bởi một đa thức tạo mã tuyến tính g(x) bậc m>0:
g(x) = gmxm + gm-1xm-1 + ..... + g1x + g0 (2.1)
Đối với các chuỗi cơ số hai (có giá tri {0,1}), gi bằng 0 hay 1 và gm = g0 = 1. Đặt g(x) = 0,
ta đƣợc sự hồi quy sau:
1= g1 x +g2x2 + ....+ gm-2xm-2 + gm-1xm-1 + xm (2.2)
vì -1 = 1 (mod 2). Với "xk" thể hiện đơn vị trễ, phƣơng trình hồi quy trên xác định các kết nối hồi
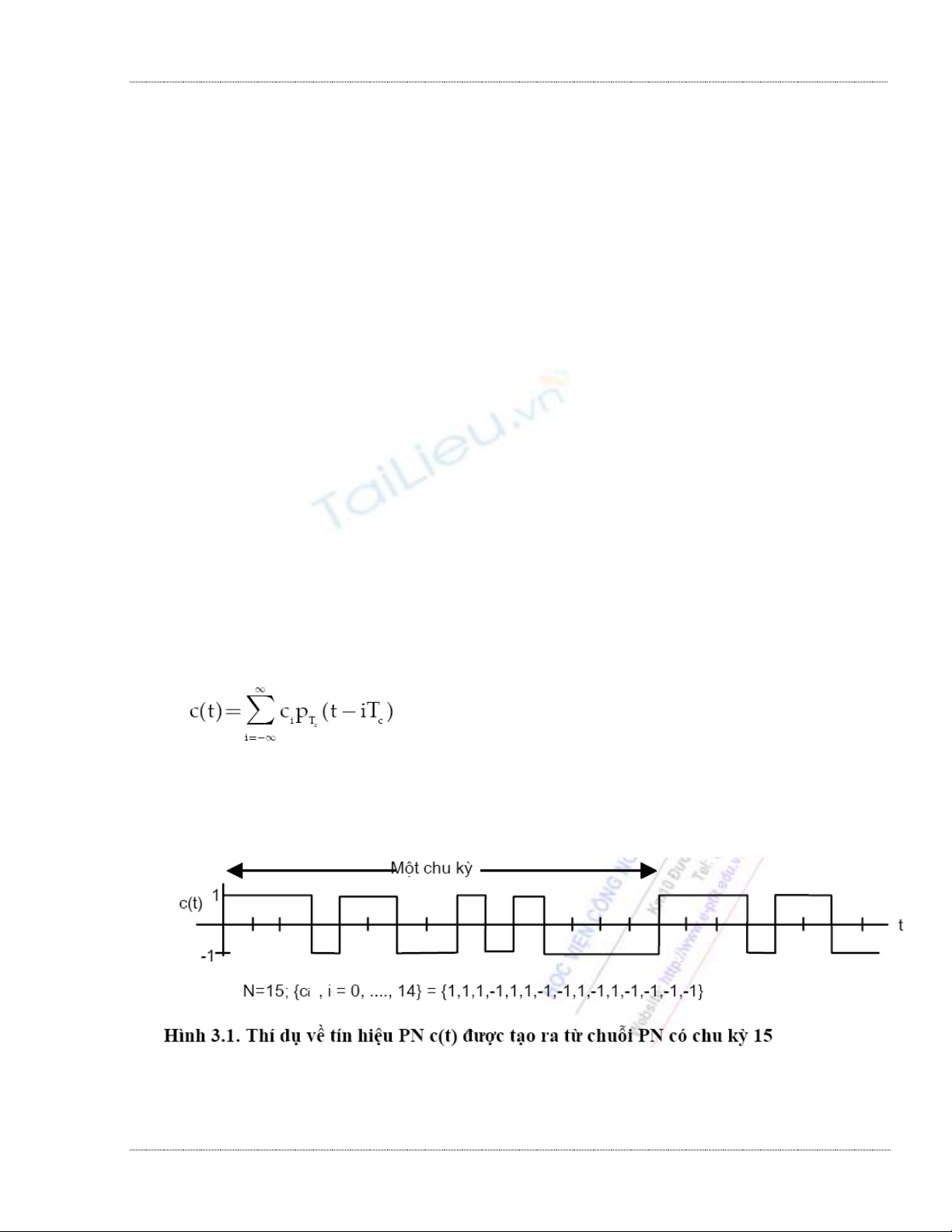
tiếp trong mạch thanh ghi dịch cơ số hai của hình 2.1. Lƣu ý rằng các cổng hoặc loại trừ (XOR)
thực hiện các phép cộng mod 2.
Nếu gi = 1 khoá tƣơng ứng của mạch đóng, ngƣợc lại nếu gi ≠ 1, khoá này hở. Để thực
hiện điều chế BPSK tiếp theo, đầu ra của mạch thanh ghi dịch phải đƣợc biến đổi vào 1 nếu là 0
và vào -1 nếu là 1. Thanh ghi dịch là một mạch cơ số hai trạng thái hữu hạn có m phần tử nhớ. Vì
thế số trạng thái khác 0 cực đại là 2m-1 và bằng chu kỳ cực đại của chuỗi ra c = (c0, c1, c2, .......).
Xét hình vẽ 2.1, giả sử si(j) biểu thị giá trị của phần tử nhớ j trong thanh ghi dịch ở xung đồng hồ
i. Trạng thái của thanh ghi dịch ở xung đồng hồ i là vectơ độ dài hữu hạn si = {si(1), si (2), ... ,
si(m)}. Đầu ra ở xung đồng hồ i là ci-m = si (m). Thay 1 bằng ci vào ptr. (2.2) ta đƣợc điều kiện hồi
quy của chuỗi ra:
ci = g1 ci-1 + g2 ci-2 + ..... + gm-1ci-m+1 + ci-m (mod 2) (2.3)
đối với i≥0. Thí dụ, xét đa thức tạo mã g(x) = x5 + x4 + x3 + x +1. Sử dụng (2.3) ta đƣợc hồi quy ci
= ci-1 + ci-3 + ci-4 + ci-5 (mod 2) và xây dựng thanh ghi dịch hồi tiếp tuyến tính ở hình 2.2. Vì bậc
của g(x) bằng m = 5, nên có 5 đơn vị nhớ ( năm phần tử thanh ghi dịch) trong mạch. Đối với mọi
trạng thái khởi đầu khác không (s0 ≠ {0, 0, 0, 0, 0}), trạng thái của thanh ghi dịch thay đổi theo
điều kiện hồi quy đƣợc xác định bởi đa thức tạo mã g(x). Trong thí dụ này chuỗi ra tuần hoàn là
cột cuối cùng ở hình 2.2: c = 111101000100101011000011100110.... Tình cờ chuỗi này có chu
kỳ cực đại và bằng N = 2m - 1. Các đa thức tạo mã khác có thể tạo ra chu kỳ ngắn hơn nhiều. Lƣu
ý rằng ở cấu hình mạch đƣợc xét này, m bit đầu tiên của chuỗi ra bằng các bit đƣợc nạp ban đầu
vào thanh ghi dịch: s0 = 11111. Đối với nạp ban đầu khác, chẳng hạn s0 = 00001, đầu ra của chuỗi
tƣơng ứng trở thành 1000011100110111110100010010101...., là dịch (sang phải N-i = 31 -18 =13
đơn vị) của chuỗi c.
Tröôøng Ñaïi Hoïc Coâng Nghieäp TP.HCM Khoa coâng ngheä ñieän töû
Chöông 6: Traûi phoå Th.S Lyù Tuù Nga
86
CHƢƠNG 3
CÁC HỆ THỐNG TRẢI PHỔ CHUỖI TRỰC TIẾP
3.1. GIỚI THIỆU CHUNG
. Các chủ đề đƣợc trình bày trong chƣơng
• Mã giả tạp âm sử dụng trong DSSS
• Hệ thống DSSS-BPSK
3.2. MÃ GIẢ TẠP ÂM SỬ DỤNG TRONG DSSS
Nhƣ đã đề cập ở chƣơng 1 và 2, ta dùng mã "ngẫu nhiên" để trải phổ bản tin ở phía phát
và giải trải phổ tín hiệu thu đƣợc ở phía thu. Mã "ngẫu nhiên" đóng vai trò trung tâm trong hệ
thống SS. Tuy nhiên nếu mã này thực sự ngẫu nhiên thì thậm chí máy thu chủ định cũng không
thể lấy ra bản tin vì không thể biết đƣợc phƣơng pháp để đồng bộ với mã thực sự ngẫu nhiên, dẫn
đến hệ thống trở nên vô dụng. Vì thế phải thay thế bằng một mã giả ngẫu nhiên. Đây là một mã
tất định biết trƣớc đối với máy thu chủ định. Nhƣng thể hiện giống tạp âm đối với các máy thu
không chủ định. Mã này thƣờng đƣợc gọi là chuỗi giả tạp âm (PN: Pseudo-Noise). Các chuỗi PN
đã đƣợc ta khảo sát kỹ ở chƣơng 1. Chuỗi PN là một chuỗi các số đƣợc lặp lại theo một chu kỳ
nhất định.
Ta sử dụng {ci , i= số nguyên} → {...,c-1 , c0 , c1 ,...} để biểu thị một chuỗi PN. Giả sử N
là chu kỳ sao cho ci + N = ci . Đôi khi ta gọi N là độ dài của chuỗi PN và một chuỗi tuần hoàn chỉ là
sự mở rộng tuần hoàn của chuỗi có độ dài N. Để một chuỗi {ci} là một chuỗi giả tạp âm tốt, giá
trị của ci phải độc lập với giá trị của cj đối với mọi i ≠ j. Để đảm bảo điều này lý tƣởng chuỗi nói
trên không đƣợc lặp lại, nghĩa là chu kỳ phải là ∞. Trong thực tế vì chuỗi PN phải tuần hoàn nên
chu kỳ của nó phải lớn để đạt đƣợc thuộc tính ngẫu nhiên tốt.
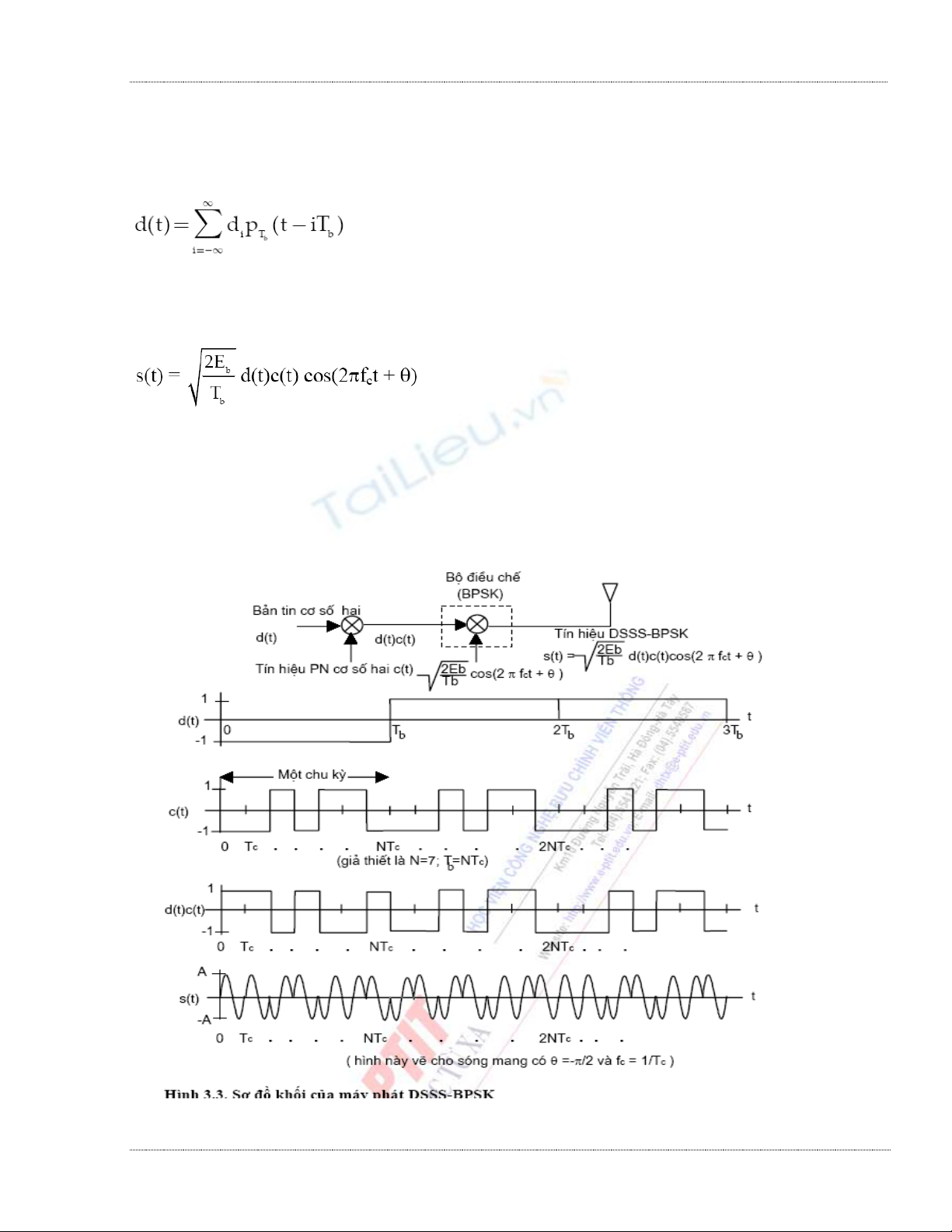
Trong một hệ thống DSSS, một tín hiệu liên tục theo thời gian đƣợc gọi là tín hiệu PN
đƣợc tạo ra từ chuỗi PN dùng để trải phổ. Giả thiết chuỗi PN này là cơ số hai, nghĩa là ci = ± 1, thì tín
hiệu PN này là
trong đó pTc(t) là xung chữ nhật đơn vị đƣợc cho bởi phƣơng trình (2.13), ci đƣợc gọi là chip và
khoảng thời gian Tc giây đƣợc gọi là thời gian chip. Lƣu ý rằng tín hiệu PN có chu kỳ là NTc. Một
thí dụ của chuỗi này đƣợc cho ở hình 3.1 đối với N = 15 và {ci , i = 0, 1, ..., 14} = {1, 1, 1, -1, 1,
1, -1, -1, 1, -1, 1, -1, -1, -1, -1}. Tín hiệu (chuỗi) PN còn đƣợc gọi là tín hiệu (chuỗi) trải phổ, tín
hiệu (chuỗi) ngẫu nhiên, và dạng sóng (chuỗi) của chữ ký (Signature).
Tröôøng Ñaïi Hoïc Coâng Nghieäp TP.HCM Khoa coâng ngheä ñieän töû
Chöông 6: Traûi phoå Th.S Lyù Tuù Nga
87
3.3. CÁC HỆ THỐNG DSSS- BPSK
3.3.1. Máy phát DSSS- BPSK
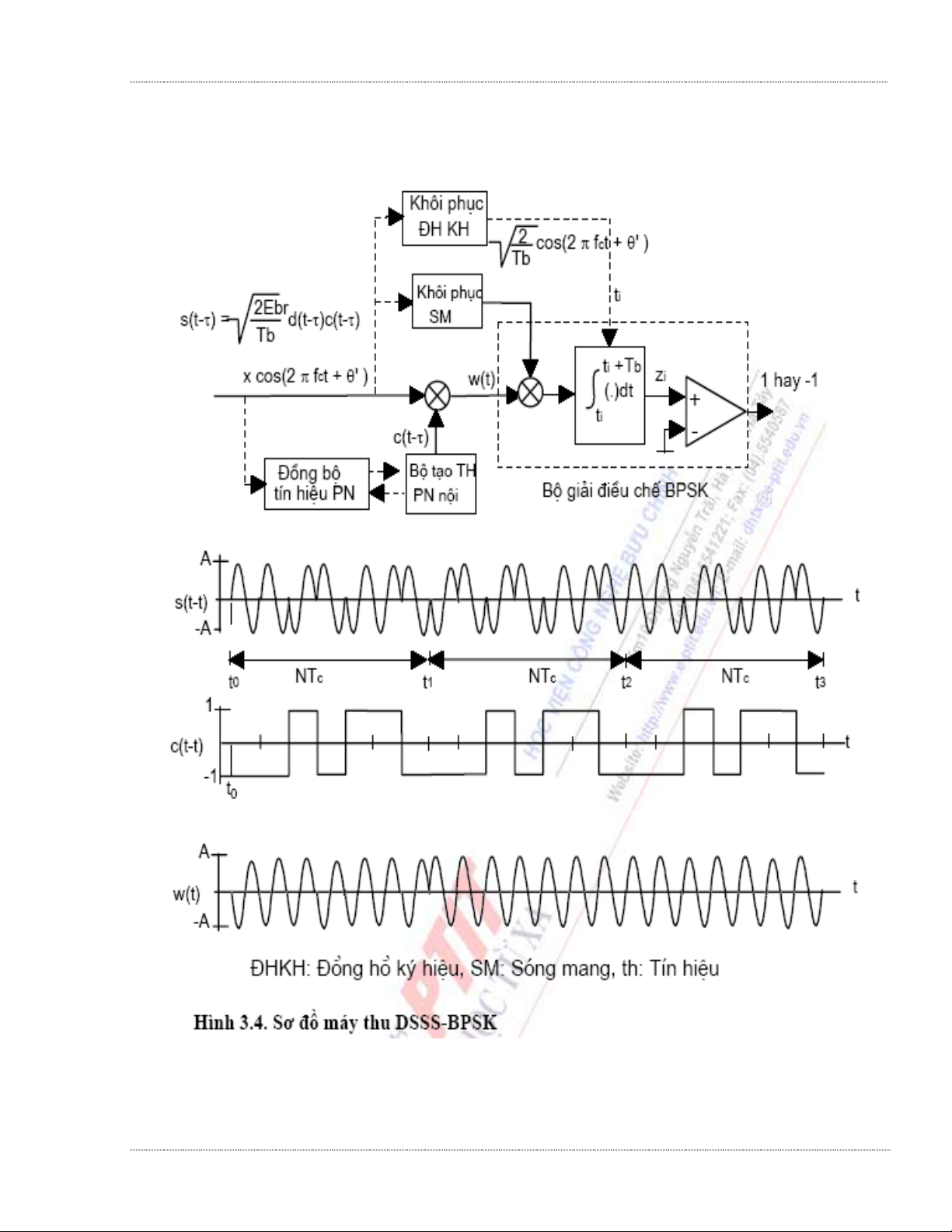
Sơ đồ khối của máy phát DS/SS sử dụng BPSK đƣợc cho ở hình 3.3. Ta có thể biểu diễn
số liệu hay bản tin nhận các giá trị ±1 nhƣ sau:
trong đó di = ±1 là bit số liệu thứ i và Tb là độ rộng của một bit số liệu (tốc độ số liệu là 1/Tb bps).
Tín hiệu d(t) đƣợc trải phổ bằng tín hiệu PN c(t) bằng cách nhân hai tín hiệu này với nhau. Tín
hiệu nhận đƣợc d(t)c(t) sau đó sẽ điều chế cho sóng mang sử dụng BPSK, kết quả cho ta tín hiệu
DSSS-BPSK xác định theo công thức sau:
(3.8)
trong đó Eb là năng lƣợng trên một bit của sóng mang, Tb là độ rộng một bit, fc tần số mang và θlà
pha ban đầu của sóng mang. Thí dụ về các tín hiệu này đƣợc vẽ trên cùng một hình.
Trong rất nhiều ứng dụng một bit bản tin bằng một chu kỳ của tín hiệu PN, nghĩa là Tb =
NTc. Ta sử dụng giả thiết này cho các hệ thống DSSS trong toàn bộ giáo trình, nếu nhƣ không có
định nghĩa khác. Trong trƣờng hợp hình 3.3 ta sử dụng N = 7. Ta có thể thấy rằng tích của d(t)c(t)
cũng là một tín hiệu cơ số hai có biên độ ±1, có cùng tần số với tín hiệu PN. Tín hiệu DSSSBPSK
nhận đƣợc đƣợc vẽ ở đồ thị cuối cùng của hình 3.3.
Tröôøng Ñaïi Hoïc Coâng Nghieäp TP.HCM Khoa coâng ngheä ñieän töû
Chöông 6: Traûi phoå Th.S Lyù Tuù Nga
88
3.3.2. Máy thu DSSS-BPSK
Sơ đồ khối của máy thu DSSS- BPSK đƣợc cho ở hình 3.4.
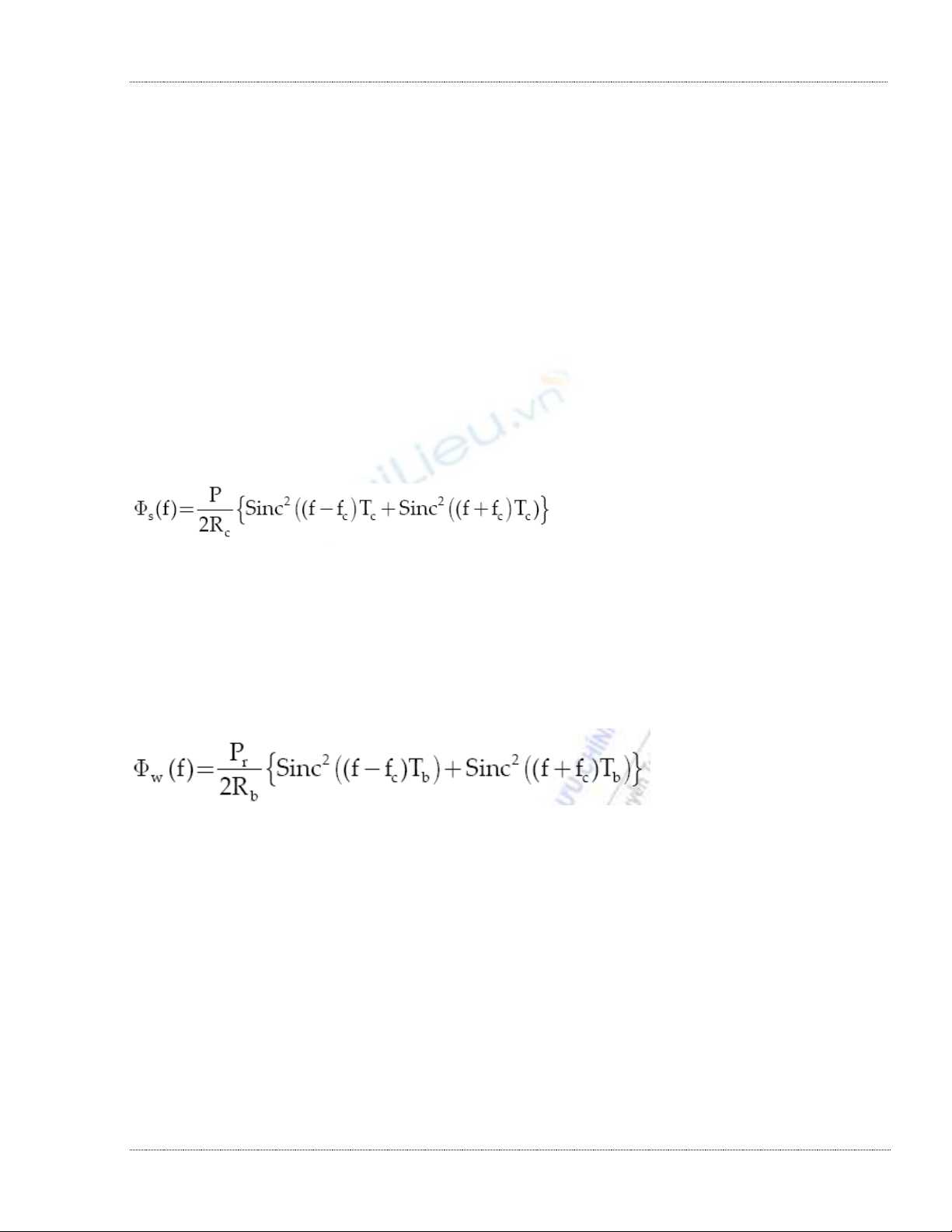
Tröôøng Ñaïi Hoïc Coâng Nghieäp TP.HCM Khoa coâng ngheä ñieän töû
Chöông 6: Traûi phoå Th.S Lyù Tuù Nga
89
3.3.3. Mật độ phổ công suất, PSD
Để có thể hiểu rõ hơn các hệ thống DSSS, bây giờ ta đi xét PSD (Power Spectral Density)
của các tín hiệu ở các điểm khác nhau trong máy phát và máy thu ở hình 3.3 và 3.2.
Ta mô hình bản tin và tín hiệu PN nhƣ là các tín hiệu cơ số hai ngẫu nhiên ( mỗi bit hay mỗi chip
nhận các giá trị +1 hay -1 đồng xác suất). Bản tin d(t) với biên độ ±1 có tốc độ bit 1/Tb bps và
PSD:
Φd(f) = TbSinc2(fTb) (3.14)
có độ rộng băng tần theo Nyquist 1/2Tb Hz, còn tín hiệu PN (với biên độ ±1) có tốc độ chip 1/Tc
và PSD là:
Φc(f) = TcSinc2(fTc) (3.15)
với độ rộng băng tần theo Nyquist 1/Tc Hz . Vì Tb/Tc là một số nguyên và vì khởi đầu của mỗi bit
d(t) trùng với khởi đầu của chip c(t) nên tích d(t)c(t) có PSD nhƣ sau:
Φdc(f) = TcSinc2(fTc) (3.16)
có độ rộng băng tần 1/Tc Hz giống nhƣ độ rộng băng tần của c(t). Vì thế quá trình trải phổ sẽ tăng
độ rộng băng tần Tb/Tc
= N lần , thông thƣờng giá trị này rất lớn. Điều chế sóng mang chuyển đổi tín hiệu băng gốc d(t)c(t) vào
tín hiệu băng thông s(t) có PSD:
(3.17)
và có độ rộng băng tần theo Nyquist 1/Tc Hz, trong đó P là công suất trung bình của tín hiệu. Thí
dụ về Φd(f), Φdc(f) và Φs(f) đƣợc cho ở hình 3.5, trong đó chúng ta sử dụng Tb/Tc = 2. So sánh
Φd(f) và Φs(f) ta thấy đại lƣợng giảm 2Tb /PTc lần và độ rộng băng tần tăng Tb/Tc lần. Vì thế
N=Tb/Tc là tỷ lệ trải phổ.
Trong máy thu tín hiệu r(t-τ) là phiên bản trễ của tín hiệu DS s(t) và có công suất thu giảm do
truyền sóng bằng Pr. Nên PSD của nó cũng giống nhƣ PSD của tín hiệu s(t) đƣợc cho ở
phƣơng trình (3.17) nhƣng với công suất P đƣợc thay bằng Pr, vì trễ không làm thay đổi phân bố
công suất ở vùng tần số. Ngoài ra PSD của c(t-τ) cũng giống nhƣ PSD của c(t) đƣợc cho ở ptr
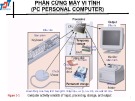
(3.15). Sau khi giải trải phổ ta đƣợc tín hiệu w(t) với PSD đƣợc xác định bởi:
(3.18)
Biểu thức trên đƣợc mô tả ở hình 3.5 (c). Ta thấy rằng Φw(f) bây giờ có PSD băng hẹp với cùng
dạng phổ nhƣ d(t) nhƣng đƣợc dịch sang trái và phải fc. Độ rộng băng tần của w(t) là 1/Tb, gấp hai lần
d(t). Điều này giống nhƣ dự tính vì w(t) giống hệt nhƣ phiên bản đƣợc điều chế của d(t).
Từ PSD cuả các tín hiệu khác nhau ta thấy rằng PSD của d(t) đƣợc trải phổ bởi c(t) và sau đó
đƣợc giải trải phổ bởi c(t-τ) ở máy thu.