Khoa CNTT - DDHBK Hà nội
hunglt@it-hut.edu.vn
8682595
1
1
Bài 4 Các phép biếnđổiĐồ hoạ
Transformations
Le Tan Hung
Email: hunglt@it-hut.edu.vn
2
Phép biếnđổi - Transformations
zTrong kỹthuậtđồ hoạ3 bước: Mô hình, Tô trát
vàHiên thị(modeling, rendering, displaying)
zVới Modeling ( Mô hình hóa) :
zTransformation: là phép ánh xạtọađộ điểm hay
vector thành tọađộ hay vector khác
modeling
coordinate Modeling
transformation
Viewing
transformation
world
coordinate
viewing
coordinate (eye
coordinate)
3
Phép biến đổi Transformations
zBiến đổi mô hình hoá - Modeling transformations
–build complex models by positioning simple
components
zBiến đổi tạo góc nhìn - Viewing transformations
–placing virtual camera in the world
–transformation from world coordinates to camera
coordinates
zBiến Phép chiếu – Projection Transform
4
Transformations - Modeling
world
5
Phép biếnđổi Affine
Affine Transformations?
zPhép biếnđổiAffine là phép biếnđổitọa độ
điểmđặctrưng củađốitượng thành tậptương
ứng các điểmmớiđể tạoracáchiệuứng cho
toàn đốitượng.
–Vídụ: phép biếnđổitọađộ vớichỉ2 điểmđầucuốicủa
đoạnthẳng tạo thành 2 điểmmớimàkhinối chúng với
nhau tạo thành đoạnthẳng mới.
zCác điểmnằmtrênđoạnthẳng sẽcó kếtquảlà
điểmnằmtrênđoạnthẳng mớivới cùng phép biến
đổi thông qua phép nộisuy.
6
Modeling Transformations
Transform
objects/points
Transform coordinate system
Khoa CNTT - DDHBK Hà nội
hunglt@it-hut.edu.vn
8682595
2
7
Biểu diễn Ma trận
zViệc biến đối các đối tượng làm thay đổi các
điểm P thành các điểm Q theo thuật toán
zViệc biến đổi P sử dụng tọa độ của P (Px,Py) ánh
xạ thành các tọa độ mới Q(Qx,Qy)
zViệc biến đổi có thể biểu diễn thông qua hàm T,
hàm ánh xạ của điểm:
–T(Px,Py) = (Qx,Qy)
–or:
–T(P) = Q
8
Matrix Representation
zPhép biến đổi đồ họa - affine transformation T ánh xạ
tập P sang tập Q:
–
–
–where a, b,c,d, tx and ty là các hệ số
zBiểu diễn ma trận:
zi.e. ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
y
x
y
x
y
x
t
t
P
P
dc
ba
Q
Q
xxxx t bP aP Q +
+
=
yyyy t dP cP Q ++=
Tr MP Q +
=
9
Các phép biếnđổihìnhhọchai
chiều
zPhương pháp biểudiễnđốitượng P = [ x y ]
zPhép biếnđổivịtrí điểm
zThực thi phép biếnđổiđúngtrên1 điểmảnh sẽđúng
trên toàn bộđốitượng
⎥
⎦
⎤
⎢
⎣
⎡
=dc
ba
T
[][][ ]
()( )
[]
[]
'' y dybx *y * xcyax
dc
ba
xTX =++=
⎥
⎦
⎤
⎢
⎣
⎡
=
y
x
z
pM
pW
10
Phép biếnđổi
zPhép bấtbiến
zPhép biếnđổitỉlệ- Scaling
zA scaling changes the size of an object with two scale
factors, Sxand Sy
zPhép biếndạng
zA shearing shears an object in a particular direction, (in
2D, it’s either in the x or in the y direction
⎥
⎦
⎤
⎢
⎣
⎡
=10
01
T
[][][ ]
()
[][]
''
10
0
** yxyax
a
yxTX ==
⎥
⎦
⎤
⎢
⎣
⎡
=
[][][ ] [ ][ ]
''
10
1
** yxdybx
b
yxTX =+=
⎥
⎦
⎤
⎢
⎣
⎡
=
x
z
y
11
Phép quay- Rotation
x = ρcos α, y = ρsin α;
x’ = ρcos (θ+α), y’ = ρsin (θ+α) ;
x’ = ρ( cosθcosα-sinθsinα)
= x cosθ- y sinθ
y’ = ρ( sinθcosα+ cosθsinα)
= x sinθ+ y cosθ
[x' y']= [xcosθ- ysinθxsinθ+ ycosθ]
y
(x, y )
x
α
ρ
θ
ρ
( x’, y’ )
⎥
⎦
⎤
⎢
⎣
⎡
−
=
θθ
θθ
cossin
sincos
][T
12
Thuộc tính cơ bản của phép biến
đổi Affine Transformations
zPreservation of lines:
–They preserve lines, so the image of a straight line is
another straight line.
–This vastly simplifies drawing transformed line
segments.
–We need only compute the image of the two endpoints
of the original line and then draw a straight line between
them
–Preservation of collinearity guarantees that polygons will
transform into polygons
–Affine transformations map lines to lines;
Khoa CNTT - DDHBK Hà nội
hunglt@it-hut.edu.vn
8682595
3
13
Thuộc tính
zPreservation of parallelism
–Preservation of parallelism guarantees that
parallelograms will transform into parallelograms
zPreservation of proportional distances
–Preservation of proportional distances means that mid-
points of lines remain mid-points
zAffine transformations change volume by |
Det(M) |;
14
Kếthợp các phép biếnđổi
Composition of Affine Transforms
zAny affine transformation can be
decomposed into elementary
transformations.
zMọi phép biếnđổiphứctạpđều
có thểtạo thành từcác phép biến
đổicơsởnhư:
–Dịch chuyển - Translation
–Tỉlệ- Scaling
–Quay- Rotation
–Biếndạng - Shearing
15
Affine transformations preserve
affine combinations
zIt is rare that we want to perform just one elementary
transformation.
zUsually an application requires that we build a
complex transformation out of several elementary
ones
–e.g. translate an object, rotate it, and scale it, all in one move
zThese individual transformations combine into one
overall transformation
zThis is called the composition of transformations.
zThe composition of two or more affine transformations
is also an affine transformation
16
Thuộc tính
zTác động lên tập các điểm đặc trưng của đối
tượng tạo thành phép biến đổi cho đối tượng
zWe have defined each transformation by their effects on
single points
zIn practice these will be applied to multiple points to
transfer entire scenes or objects made up of many
defining points
T
17
Điểm gốc - Pivotal points
Cho phép quay và tỉ lệ Rotation and Scaling
zThe simple versions of rotation and scaling have been based around the
origin.
zThis means that when we rotate or scale, the object will also move, with
respect to the origin
zTranslate all points through (-c1,-c2)
zRotate all points about the origin by
zTranslate all points back through (c1,c2)
(c1,c2)
(0,0) 18
Pivotal points
zOften we wish to rotate or scale with respect to some
pivotal point, not the origin
zMost significantly, we often wish to rotate or scale an
object about its centre, or midpoint
zIn this way, the object’s location does not change
zTo do this, we relate the rotation or scaling about the
pivotal point V, to an elementary rotation or scaling about
the origin
–We first translate all points so that V coincides with the origin
–We then rotate or about the origin
–then all points are translated back, so that V is restored to its
original location
Khoa CNTT - DDHBK Hà nội
hunglt@it-hut.edu.vn
8682595
4
19
Hệ toạ độ đồng nhất
zVấn đề gặp phải:
zAn affine transformation is composed of a linear
transformation followed by a translation
zUnfortunately, the translation portion is not a
matrix multiplication but must instead be added as
an extra term, or vector
zWhat we need is a “trick”, so that translations can
be represented in matrix multiplication form
zThis then means that they can be easily
composed with other transformations, by simply
multiplying the matrices together 20
Tọađộ đồng nhất
Homogeneous Transform
–x' = ax + by + n
–y' = cx + dy + m
zPhương pháp biểudiễnmởrộng thông qua
tọađộ đồng nhấtcủa các vector vịtrí
zVớiứng dụng của phép chiếuhìnhhọcmà
ở đótọađộ điểmđượcmôtảdướima trận[
x* y* h]
–với x = x*/h, y = y*/h, z = z*/h và h là mộtsố
thựctuỳý
21
ƯuđiểmcủaHệtọađộ đồng nhất
Homogeneous Transform
zÐưaracáinhìnhợpnhấtcủa các phép biếnđổi
dưới phép nhân ma trận, hỗtrợcho việcxửlý
bằng cảphầncứng và phầnmềm
zKếthợp các các phép biếnđổitạo thành ma trận
tích đơngiản duy nhất. Tránh nhầmlẫnvềthứtự
của các phép nhân khi sửdụng.
–Order matters: AB is generally not the same as BA
zCho phép kếthợpvớicảcác phép biếnđổiđặc
biệt không tuyến tính khác(non-affine) như:
–Phép chiếuphốicảnh - Perspective projections!
–Uốn - Bends, Vuốt tapers v.v.v
22
Phép biếnđổivớitọađộ đồng nhất
zMa trậnbiếnđổiđồng nhất
zPhép tịnh tiến⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
1
0
0
][
nm
dc
ba
T
]1[
1
010
001
]1[]1''[ nymx
nm
yxyx ++=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
(tx, ty, tz)
23
Phép tỉlệ
]12.1.[
100
020
001
]1[]1''[ SySxS
S
yxyx =
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
24
Phép quay
y
(x, y )
x
α
ρ
θ
ρ
( x’, y’ )
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−=
100
0cossin
0sincos
]1[]1''[
φφ
φφ
yxyx
]1cos.sin.sin.cos.[
φφφφ
yxyx +−=
Khoa CNTT - DDHBK Hà nội
hunglt@it-hut.edu.vn
8682595
5
25
Phép biếnđổitổng hợp
26
Ma trận biến đổi 3 chiều
3D Matrix Transformations
zCác phép biến đổi chuyển vị - translation, tỉ lệ-
scaling và quay-rotation sử dụng trong không
gian 2D đều co thể mở rộng trong không gian 3D
zAgain, using homogeneous coordinates it is
possible to represent each type of transformation
in a matrix form
zIn 3D, each transformation is represented by a
4x4 matrix
27
Các phép biếnđổihìnhhọc3 chiều
zBiểudiễnđiểm trong không gian 3 chiều
z[ x* y* z* h ] = [ x y z 1 ]. [ T ]
z[x' y' z' 1 ]= [ x*/h y*/h z*/h 1 ][ T ]
zMa trậnbiếnđổi
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
snml
rjig
qfed
pcba
][T
28
Phép tịnh tiến
–[X'] = [ X ] . [ T(dx,dy,dz) ]
–[ x' y' z' 1 ] =
–[ x y z 1 ].[ T(dx,dy,dz) ]
z= [ x+dx y+dy z+dz 1 ]
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
1
0100
0010
0001
)],,([
dzdydx
dzdydxT
29
Phép tỉlệ
zs1, s2, s3 là các hệsốtỉlệ
tương ứng trên các trụctoạđộ
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
1000
0300
0020
0001
11 s
s
s
zyxzyx ][]'''[
]13.2.1.[ szsysx=
30
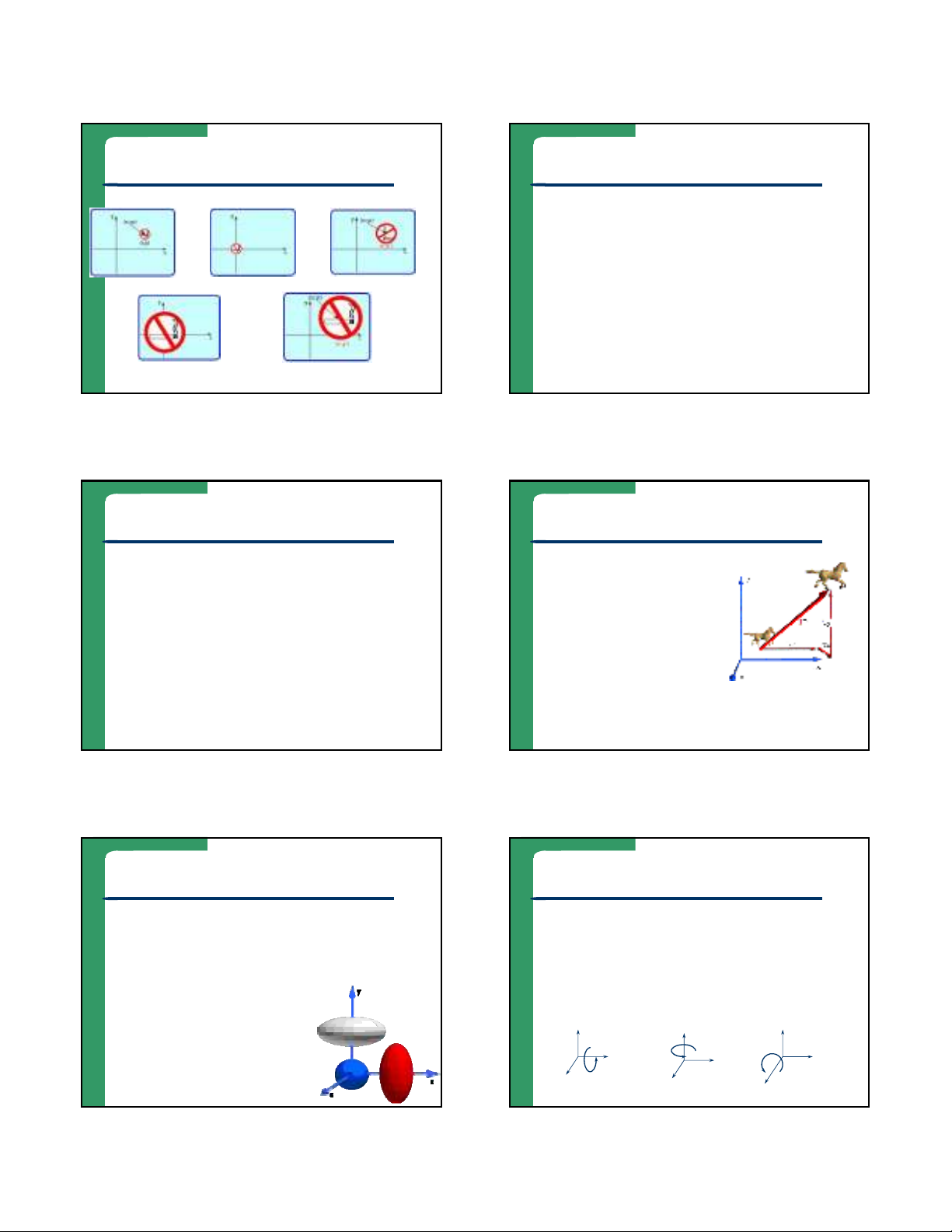
Rotation
zIn 2D, the only rotation possible was about the
origin.
zIn 3D, there are 3 possible rotations, one about
each of the x, y and z axes
zPositive rotations are anti-clockwise, negative
rotations are clockwise, when looking down a
positive axis towards the origin
x
y
z
x
y
z
x
y
z


























