95
CHƯƠNG 5. TÍN HIỆU XUNG VÀ MẠCH RLC
Mở đầu
Kỹ thuật xung là phần kiến thức khá quan trọng đối với toàn bộ chương trình học của sinh
viên ngành Điện tử. Chương 5 sẽ cung cấp cho sinh viên các kiến thức cơ bản: khái niệm và
thông số của tín hiệu xung; sơ đồ, nguyên lí hoạt động và ứng dụng của các mạch biến đổi dạng
xung. Trong thực tế, từ một tín hiệu xung đã có, có thể yêu cầu cần một tín hiệu xung có hình
dạng khác (xung vuông, xung tam giác, xung nhọn….) để thực hiện các chức năng khác nhau.
Mục tiêu chương 5: sinh viên có khả năng:
- Nhận diện được các dạng xung, xác định được các thông số của tín hiệu xung.
- Nhận diện được các mạch biến đổi dạng xung (mạch tích phân, mạch vi phân). Phân tích
được nguyên lí hoạt động, xác định được dạng tín hiệu ra theo tín hiệu vào trong từng trường
hợp cụ thể. Ứng dụng được các mạch biến đổi dạng xung theo yêu cầu cụ thể.
- Thiết kế các mạch biến đổi dạng xung theo yêu cầu kỹ thuật cho trước.
5.1. Khái niệm và các dạng xung
- Các tín hiệu điện có biên độ thay đổi theo thời gian được chia ra 2 loại cơ bản: tín hiệu liên
tục (tín hiệu tương tự hay tín hiệu tuyến tính) và tín hiệu gián đoạn (tín hiệu xung hay số)
- Tín hiệu xung dòng điện hoặc điện áp là những tín hiệu có thời gian tồn tại rất ngắn, có thể so
sánh với quá trình quá độ trong mạch điện mà chúng tác dụng.
Trong mạch điện có thể tác động 1 xung hoặc 1 dãy xung.
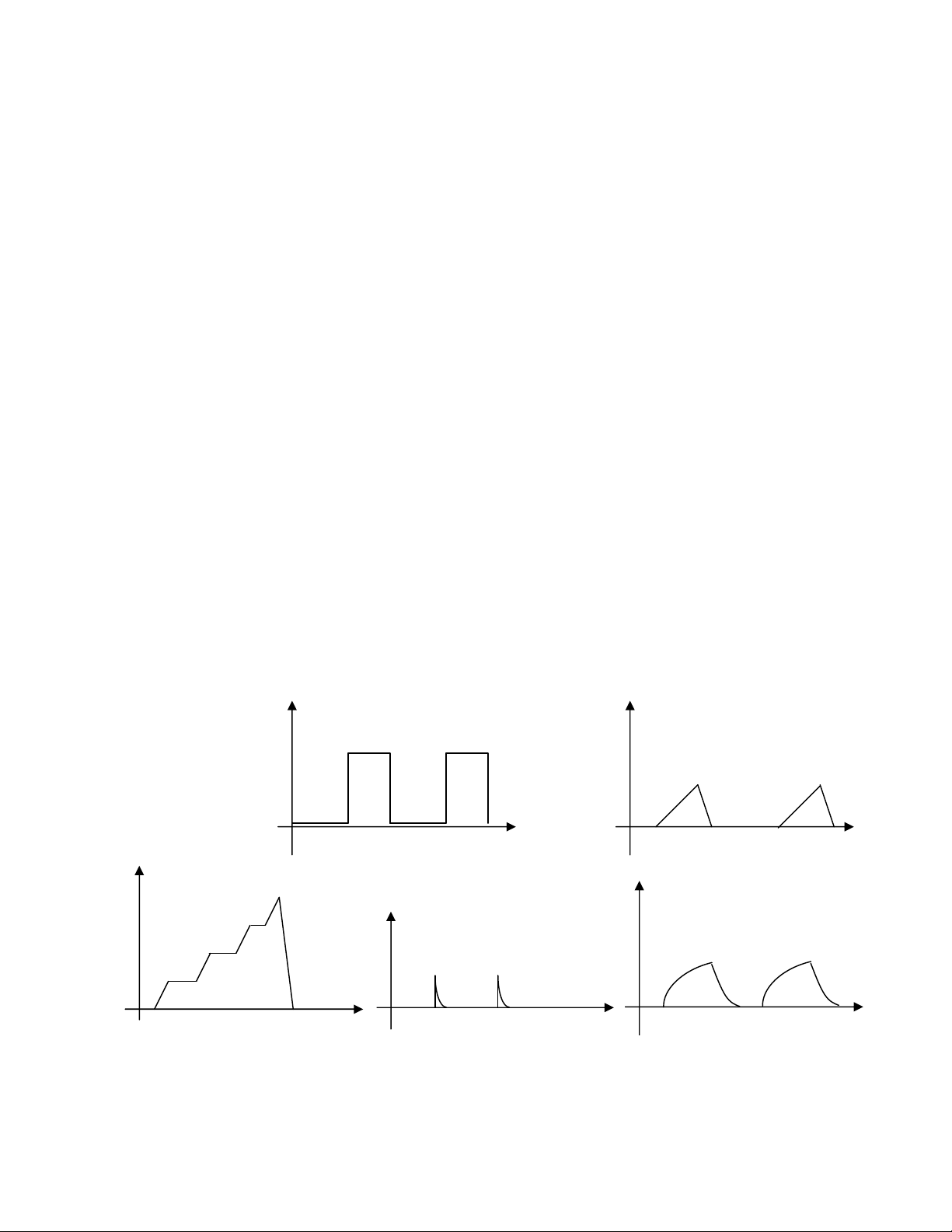
Các dạng xung
- Có nhiều dạng tín hiệu xung: xung vuông, xung tam giác, xung răng cưa, xung nhọn, xung
nấc thang…
Nhận xét: Các dạng xung cơ bản rất khác nhau về dạng sóng, nhưng có điểm chung là thời
gian tồn tại xung rất ngắn hay sự biến thiên từ thấp lên cao (như xung nhọn) hay từ cao xuống
thấp (như xung tam giác) xảy ra rất nhanh.
Trong nhiều trường hợp xung tam giác có thể gọi là xung răng cưa và ngược lại.
v
VH
VL
t
xung vuông
v
t
xung tam giác
v
t
xung nấc thang
v
t
xung răng cưa
v
t
xung nh
ọn
96
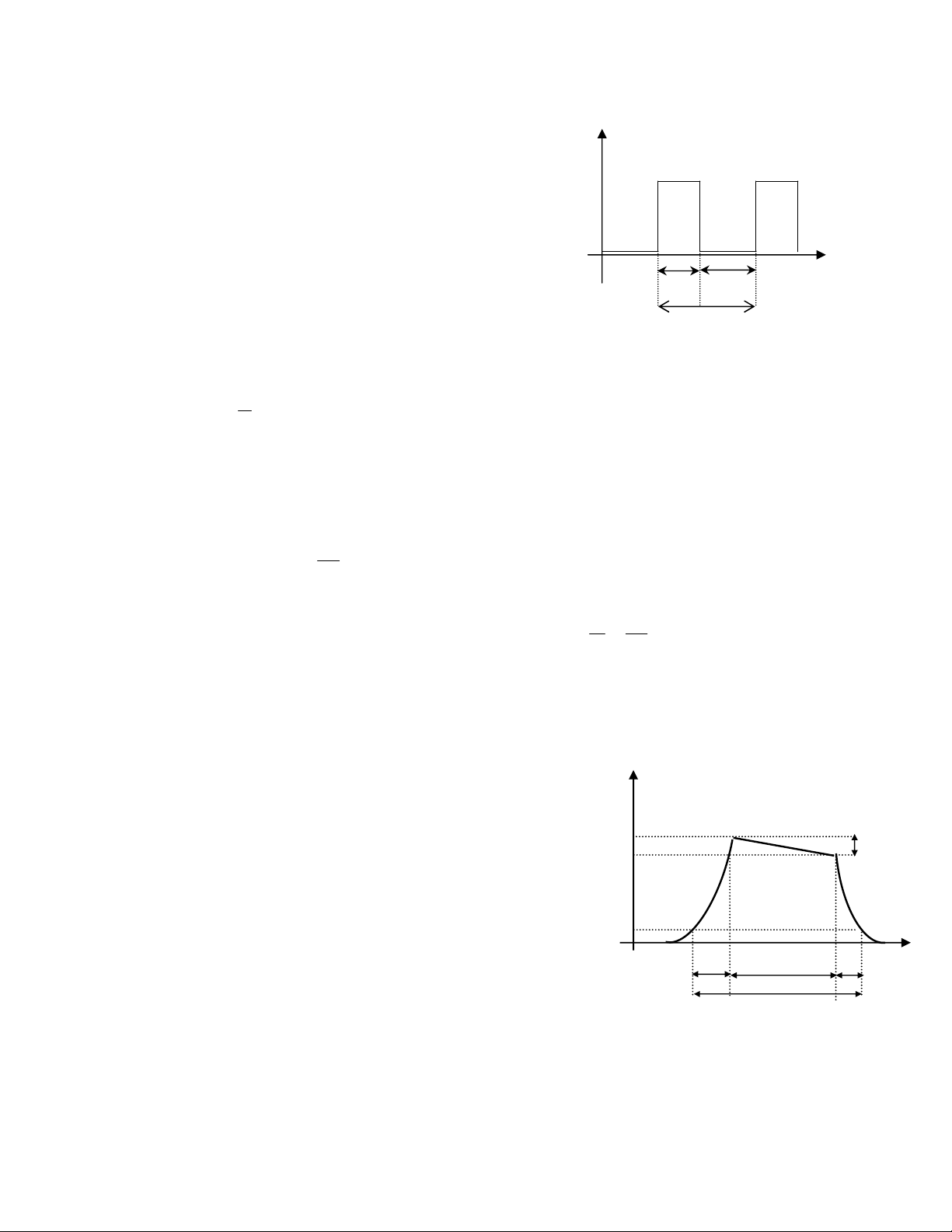
5.2. Các thông số tín hiệu xung
1) Chu kỳ xung - tần số xung
* Chu kỳ xung là : T = ton + toff
* Tần số xung: là số lần xung xuất hiện trong 1 đơn vị thời gian, và được tính theo công
thức: F=
T
1
2) Độ rỗng và hệ số đầy của xung
Trong một chu kỳ của xung, thời gian có xung (ton) thường rất ngắn so với chu kỳ T.
Định nghĩa độ rỗng của xung: là tỉ số giữa chu kỳ T và độ rộng xung ton
Q =
on
t
T
Hệ số lấp đầy của xung: là nghịch đảo của độ rỗng Q : n = T
t
Q
on
1
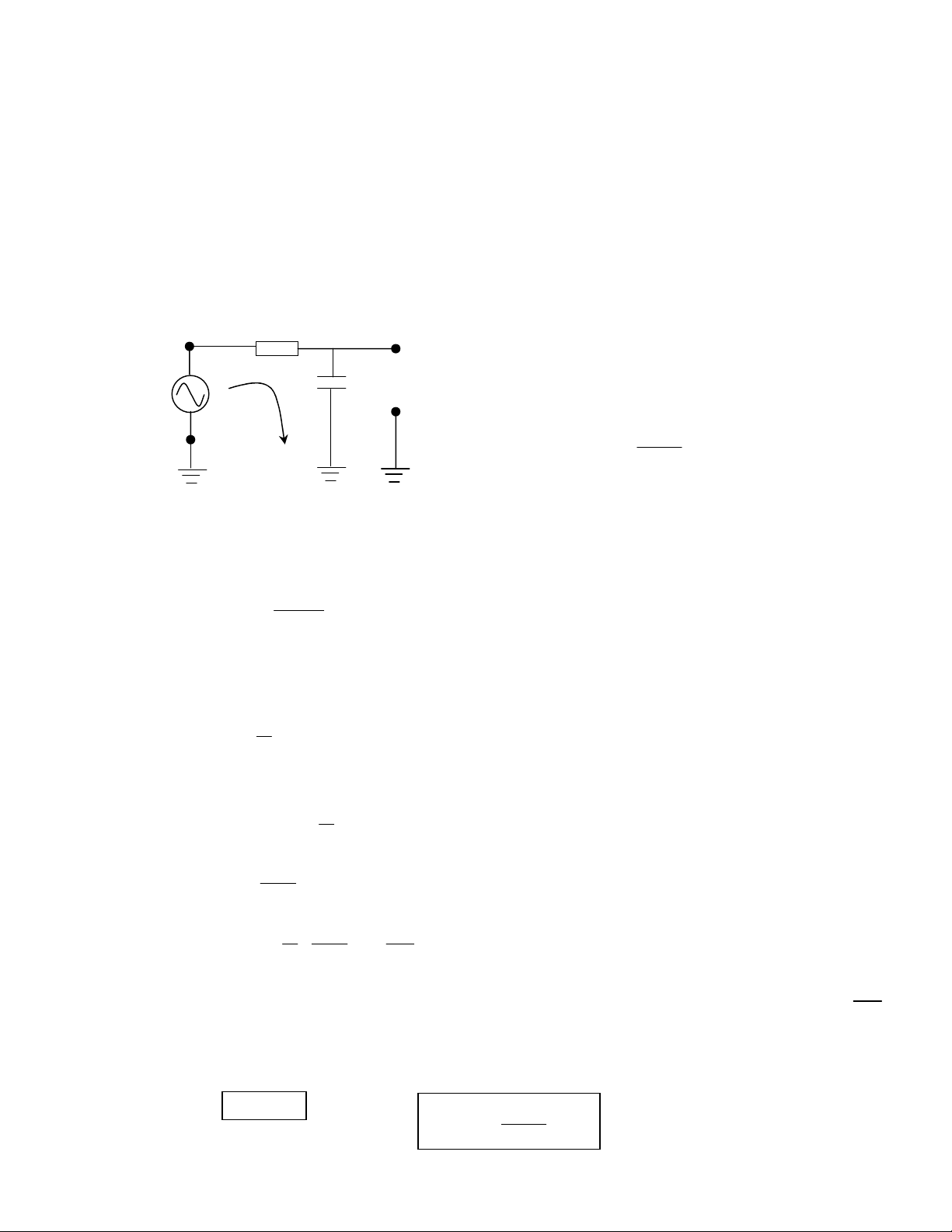
3) Độ rộng sườn trước, độ rộng sườn sau
Trong thực tế khó có một tín hiệu xung vuông lý tưởng có đường biên độ tăng và đường
biên độ giảm thẳng đứng.
Độ rộng sườn trước, độ rộng sườn sau là thời gian biên độ xung tăng hay giảm trong khoảng
0,1Vm đến 0,9Vm.
Thời gian xung có biên độ từ 0,9Vm đến Vm ứng với đoạn đỉnh của xung gọi là tp.
Độ rộng xung thực tế là: ton = tr + tp + tf
v
VH
V
L
t
t
on
t
off
T
- Độ rộng xung ton hay tx: là th
ời gian ứng
v
ới mức cao của tín hiệu (vd mức điện áp
cao) (hay thời gian tồn tại của xung).
- Th
ời gian không có xung ứng với mức thấp
của tín hiệu (vd điện áp thấp) thì gọi là t
off
hay tng (thời gian nghỉ của xung)
Theo dạng xung hình bên, khi tăng điện
áp sẽ có thời gian trễ tr gọi là độ rộng sườn
trước. Ngược lại khi giảm điện áp cũng sẽ có
thời gian trễ tf gọi là độ rộng sườn sau.
t
V
v(t)
ton
tr tp tf
V
m
0.9Vm
97
Độ sụt đỉnh xung V là độ giảm biên độ ở phần đỉnh xung.
5.3. Mạch tích phân
- Mạch tích phân là mạch mà điện áp ra v0(t) tỉ lệ với tích phân theo thời gian của điện áp
vào vi(t): v0(t) = k.vi(t)dt với k: hệ số tỉ lệ.
- Ứng dụng: + tạo xung quét (xung răng cưa)
+ biến đổi tương tự số.
+ thực hiện phép tích phân trong máy tính điện tử.
5.3.1. Mạch tích phân RC
Ta có: vi(t) = vR(t) + vC(t).
Nguồn điện áp vào vi(t) có tần số fi.
Xét trường hợp fi >>fC
Mà XC = Cfi.2
1
R >> XC (nhân cả 2 vế với i(t)) vR(t) >> vC(t).
Điện áp trên tụ được tính theo công thức:
vC(t) =
C
1.i(t)dt
Điện áp trên tụ cũng là điện áp ra, nên ta có:
v0(t) = vC(t) =
C
1.i(t)dt
trong đó i(t) =
R
tvi)( (Vì R>>XC bỏ qua XC)
Suy ra: v0(t) =
dttv
RC
dt
R
tv
C
i
i)(
1
)(
1
Như vậy, điện áp ra v0(t) là tỉ lệ với tích phân của điện áp vào vi(t) với hệ số tỉ lệ k =
RC
1
khi tần số fi >> fC.
Vậy điều kiện của mạch là:
hay
Nói cách khác:
R
v
0
v
i
C
i
Mạch tích phân chính là mạch
lọc thấp qua dùng RC với tần số
cắt:
fC =
RC
2
1
fi >> fC
fi >>
RC
2
1
98
hay
trong đó = RC là hằng số thời gian.
Ti : chu kỳ
Trường hợp điện áp vào vi là tín hiệu hình sin:
vi(t) = Vm.sin t.
v0(t) = tosc
RC
V
dttV
RC
m
m
.)sin(.
1
v0(t) = )90sin(. 0
t
RC
Vm
Kết luận: Nếu thoả mãn điều kiện của mạch tích phân như trên thì điện áp ra bị trễ pha
900 và biên độ giảm xuống với hệ số tỉ lệ là
RC
1 so với điện áp vào.
*Trường hợp điện áp vào là tín hiệu xung vuông.
Khi điện áp vào là tín hiệu xung vuông có chu kỳ là Ti thì có thể xét tỉ lệ hằng số thời
gian = RC so với Ti để giải thích các dạng sóng ra theo hiện tượng nạp xả của tụ.
RC >>
i
f
2
1 >>
i
f
2
1=
2
i
T
99
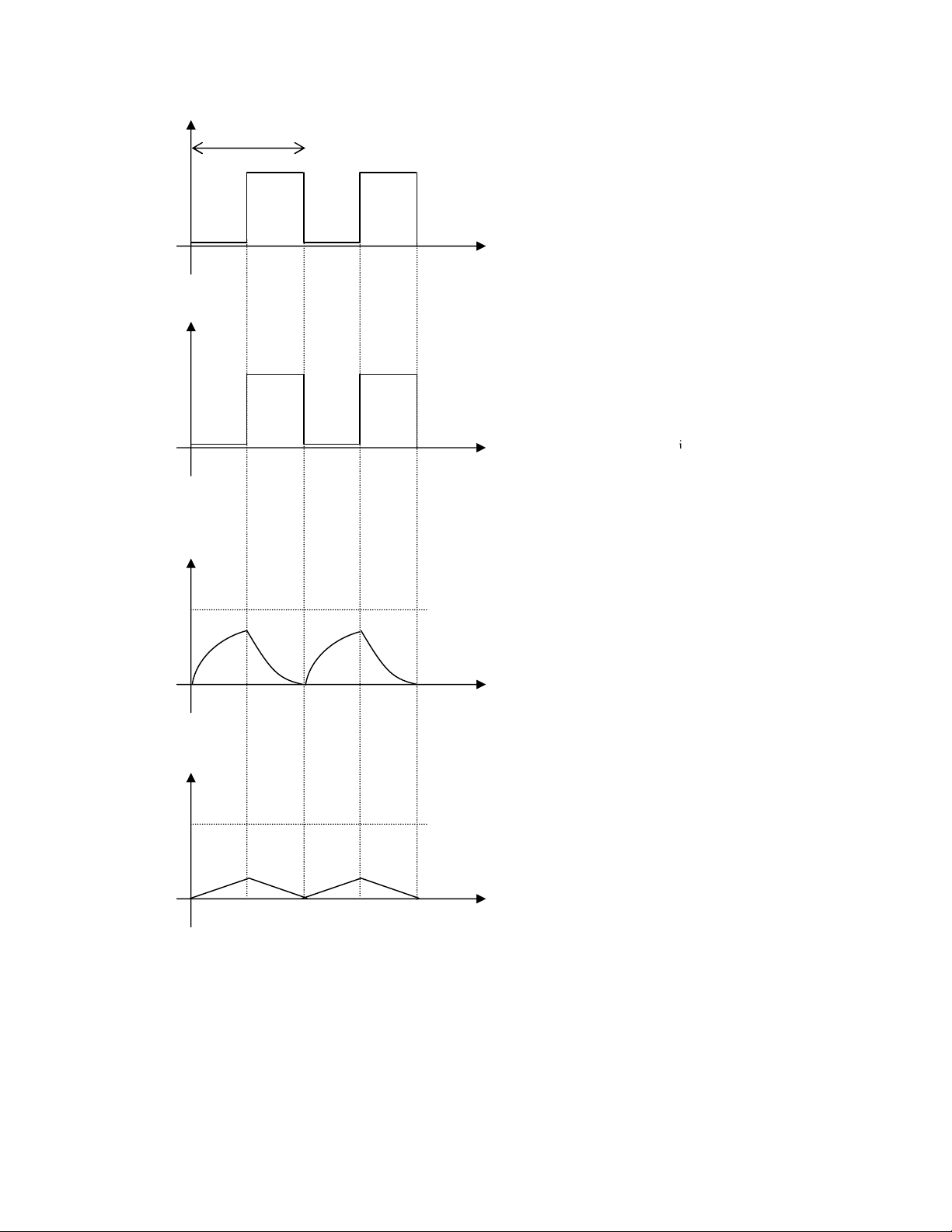
Như vậy, mạch tích phân nếu chọn trị số RC thích hợp thì có thể sửa dạng xung vuông ở
ngõ vào thành dạng sóng răng cưa hay tam giác ở ngõ ra. Nếu xung vuông đối xứng thì xung
tam giác ra là tam giác cân.
Nếu mạch tích phân có hằng số thời
gian = RC rất nhỏ so với Ti, tụ nạp
và xả rất nhanh nên điện áp ngõ ra
v0(t) có dạng giống như dạng của
đ
i
ện áp v
ào v
i
(t).
Nếu mạch tích phân có hằng số thời
gian = Ti/5, tụ nạp và xả theo dạng
hàm mũ, biên độ của điện áp ngõ ra
v0(t) thấp hơn VP
Nếu mạch tích phân có hằng số thời
gian >>Ti thì tụ nạp rất chậm nên
điện áp ra có biên độ rất thấp, nhưng
đường tăng giảm điện áp gần như
đường thẳng.
Giả thiết, điện áp ngõ vào là tín
hiệu xung vuông đối xứng
(ton = toff ) có chu kỳ Ti.
v
i
(t)
V
P
t
Ti
a) Dạng sóng ngõ vào
v
0
(t)
VP
t
b) Dạng sóng ngõ ra khi
<<Tt
v
0
(t)
VP
t
c) Dạng sóng ngõ ra khi
=Tt/5
v
0
(t)
V
P
t
d) Dạng sóng ngõ ra khi
>>Ti