KỹthuậtĐiều khiểntựđộng
Tính ổnđịnh
Tính điều
khiểnđược
Tính quan
sát được
ThS. Đỗ Tú Anh
Bộmôn Điềukhiểntựđộng
Khoa Điện, Trường ĐHBK HN
cuu duong than cong . com
15-1
Tính ổnđịnh
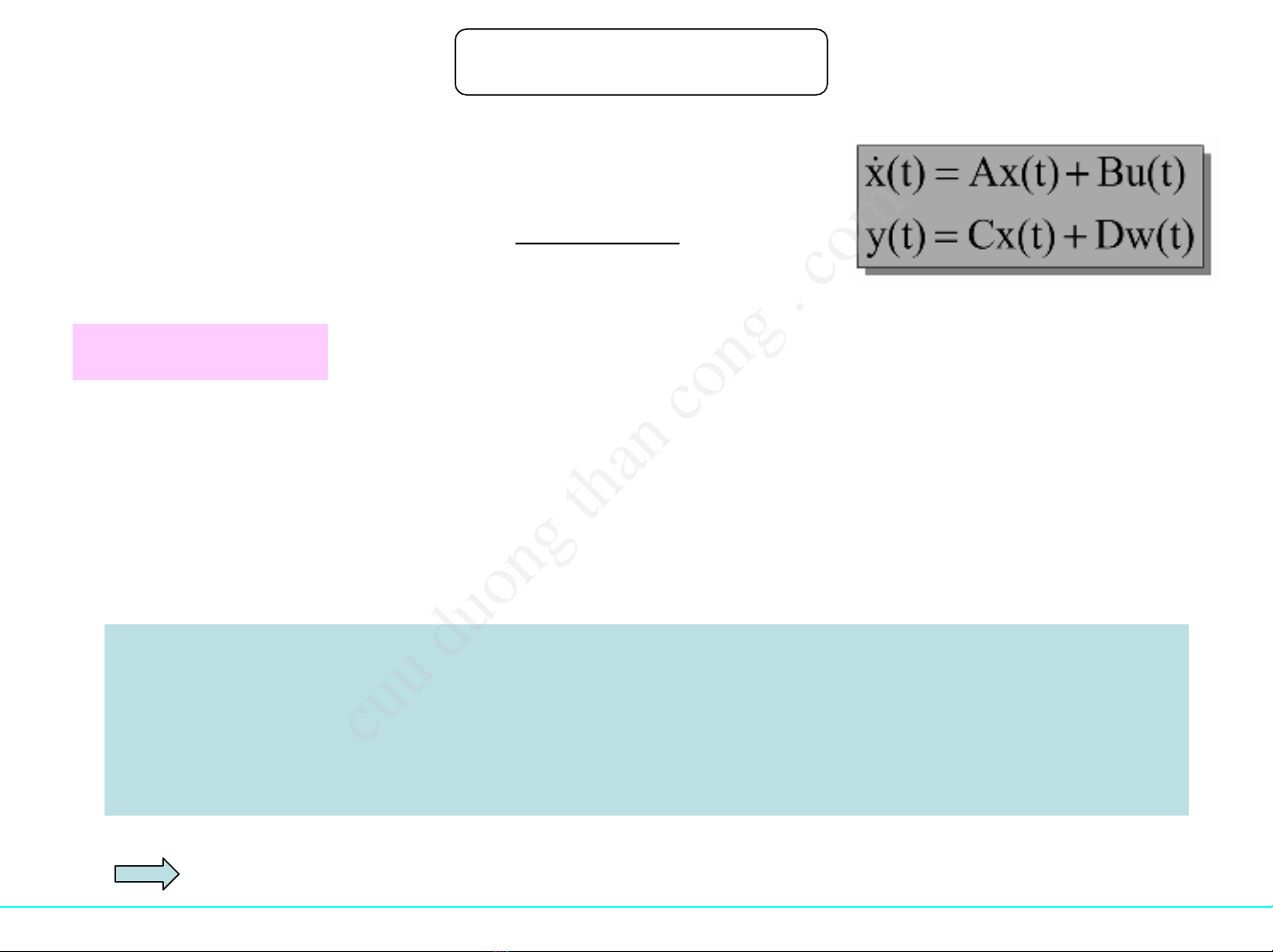
1()
() ( ) det( )
adj sI A
Gs CsI A B D C B D
sI A
−
−
=
−+= +
−
Ổnđịnh BIBO
(2) (1)
Mộthệthống đượcgọilàổnđịnh BIBO nếu khi kích thích hệbằng tín hiệu
u(t) bịchặnởđầuvàothìhệsẽcó đáp ứng y(t) ởđầuracũng bịchặn(tấtcả
các điểmcựccủahệđềunằmởnửa bên trái mặtphẳng phứcs).
Từ(2) suy ra
Hệ(1) ổnđịnh BIBO khi và chỉkhi ma trậnA cótấtcảcác giá trịriêng
nằm bên trái trụcảo, tức là khi và chỉkhi
() det( )
p
ssIA=−
có tấtcảcác nghiệmcóphầnthựcâm.
Có thểsửdụng các tiêu chuẩn Routh, Hurwitz được không???
Kỹthuật ĐKTĐ Bộmôn ĐKTĐ-Khoa Điện
cuu duong than cong . com
15-2
Tính ổnđịnh (tiếp)
Ổnđịnh Lyapunov
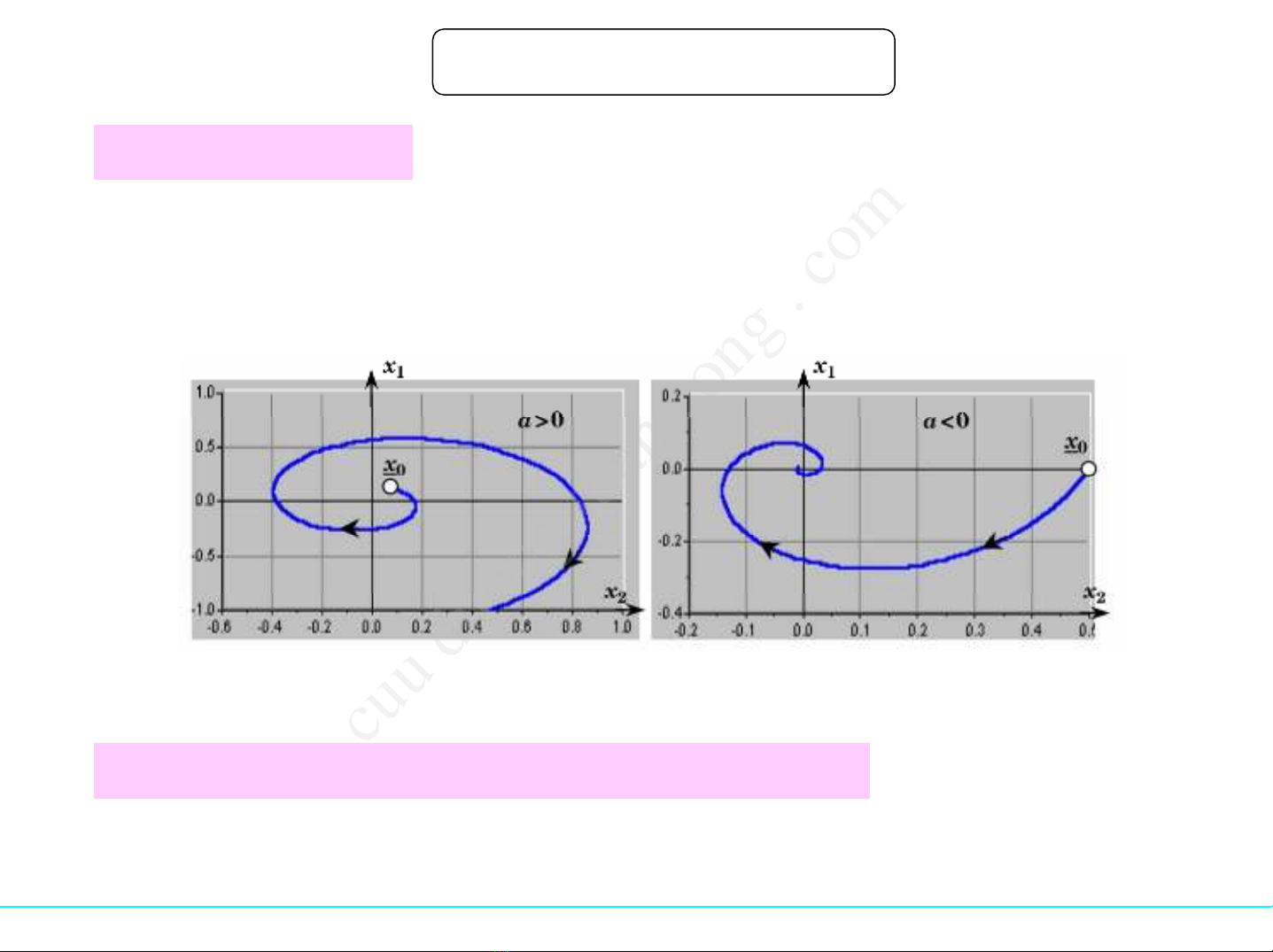
Hệổnđịnh tiêm cận Lyapunov (cũng chính là ổnđịnh BIBO) khi và chỉ
khi các quỹđạotrạng thái tựdo có hướng tiếnvềgốctọađộ và kết thúc
tạiđó.
Không ổnđịnh Ổnđịnh
Hàm Lyapunov và tiêu chuẩnổnđịnh Lyapunov
Đọctàiliệu
Kỹthuật ĐKTĐ Bộmôn ĐKTĐ-Khoa Điện
cuu duong than cong . com
15-3
Tính điềukhiểnđược
Định nghĩa
Mộthệthống tuyếntínhliêntụcđgl điềukhiểnđượcnếutồntạiítnhất
một tín hiệuđiềukhiểnđưađượcnótừmộtđiểmtrạng thái ban đầu0
x
(tùy ý) vềđượcgốctọađộ 0trong khoảng thờigianhữuhạn
Hệđgl điềukhiểnđược hoàn toàn tại0
x
nếuvớimộtđiểmtrạng thái đích
T
x(tùy ý), nhưng cho trước, luôn tồntạimộttínhiệuđiềukhiển()ut
đưahệtừ0
xtớiđược
T
xtrong khoảng thờigianhữuhạn
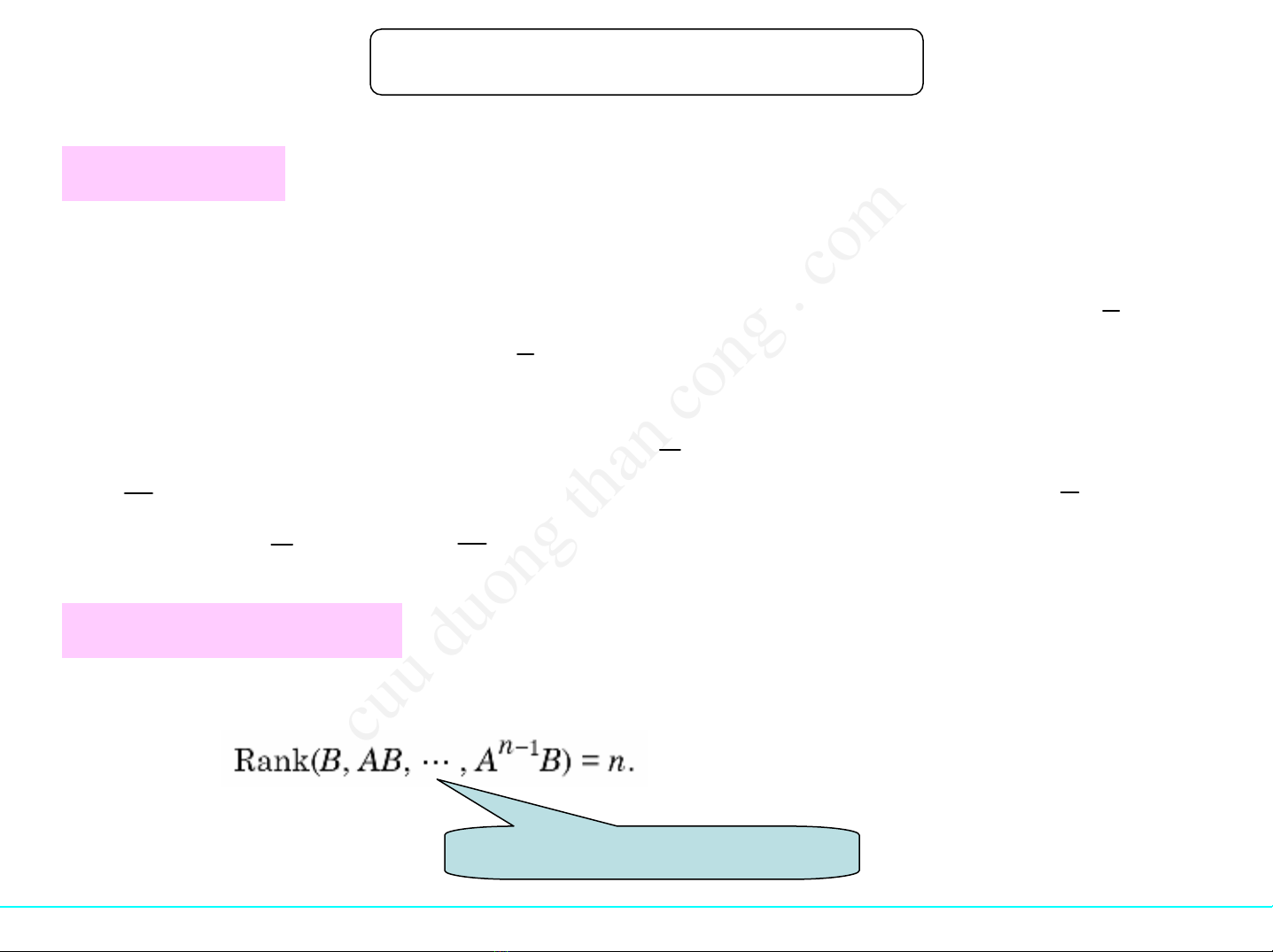
Tiêu chuẩnKalman
Cầnvàđủ để hệliên tụctuyến tính (1) điềukhiểnđượclà
Ma trậnđiều khiểnđược
Kỹthuật ĐKTĐ Bộmôn ĐKTĐ-Khoa Điện
cuu duong than cong . com
15-4
Tính điềukhiểnđược (tiếp)
Kỹthuật ĐKTĐ Bộmôn ĐKTĐ-Khoa Điện
cuu duong than cong . com