Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
336
ĐIỀU KHIỂN BALLBOT DI CHUYỂN CÂN BẰNG
TRÊN MẶT PHẲNG NGHIÊNG
Nguyễn Thị Thúy Hằng
Trường Đại học Thủy lợi, email: hangntt@tlu.edu.vn
1. GIỚI THIỆU VỀ BALLBOT
Thời gian gần đây, các các nhà nghiên cứu
đã sử dụng nhiều phương pháp điều khiển
Ballbot (robot cân bằng trên một quả bóng
hình cầu) di chuyển trên mặt phẳng ngang: từ
việc áp dụng các bộ điều khiển đơn giản như
PID [1], LQR [2], đến việc sử dụng các bộ
điều khiển phi tuyến như điều khiển trượt
tầng HSMC[3]. Nhưng phần lớn các nghiên
cứu này chỉ tập trung vào Ballbot di chuyển
trên mặt phẳng ngang, nơi thế năng của quả
bóng không đổi và điểm cân bằng của thân là
vị trí trùng với phương thẳng đứng.
Khả năng di chuyển linh hoạt và tự cân
bằng trên mặt phẳng nghiêng là một ưu điểm
lớn của Ballbot. Một số nghiên cứu trước đây
đã xây dựng mô hình Ballbot di chuyển trên
dốc và thiết kế các bộ điều khiển LQR [4].
Nhưng việc áp dụng các bộ điều khiển này
căn cứ theo mô hình tuyến tính hóa gây ra sai
số khi tính toán tín hiệu điều khiển, đặc biệt
khi Ballbot hoạt động xa điểm làm việc dùng
để tuyến tính hóa. Do đó, việc áp dụng điều
khiển phi tuyến sẽ cho phép xây dựng trực
tiếp tín hiệu điều khiển thông qua mô hình
toán học, giảm thiểu sai số do tuyến tính hóa.
Trong nghiên cứu này, tác giả đề xuất áp
dụng bộ điều khiển trượt SMSs (two-layer
Sliding Mode Surfaces) để đảm bảo sự hội tụ
của cả 2 thông số của Ballbot khi di chuyển
trên mặt phẳng nghiêng: vị trí p và góc lệch
dựa vào một tín hiệu điều khiển duy nhất.
Đồng thời áp dụng xây dựng mô hình giả vật
lý của Ballbot trên Simscape nhằm kiểm
chứng tính đúng đắn của mô hình toán học.
2. MÔ HÌNH TOÁN HỌC CỦA BALLBOT
KHI DI CHUYỂN TRÊN MẶT PHẲNG
NGHIÊNG
Mô hình toán học của Ballbot được phát
triển dựa trên mô hình 2D bằng cách tách
Ballbot thành ba mặt phẳng riêng biệt, như
vậy mô hình toán học sẽ trở nên đơn giản hơn
do giảm được số bậc tự do của ballbot từ 5
xuống còn 2. Tác giả đưa ra một số giả định
nhằm loại bỏ những ảnh hưởng không mong
muốn đến mô hình như sau:
Tiếp xúc giữa bóng và mặt đất, bóng và
cơ cấu truyền động là điểm-điểm.
Không xảy ra trượt giữa các mặt tiếp xúc.
Bỏ qua độ trễ của cơ cấu chấp hành với
tín hiệu điều khiển.
Góc nghiêng của dốc được biết trước và
giữ trong suốt quá trình.
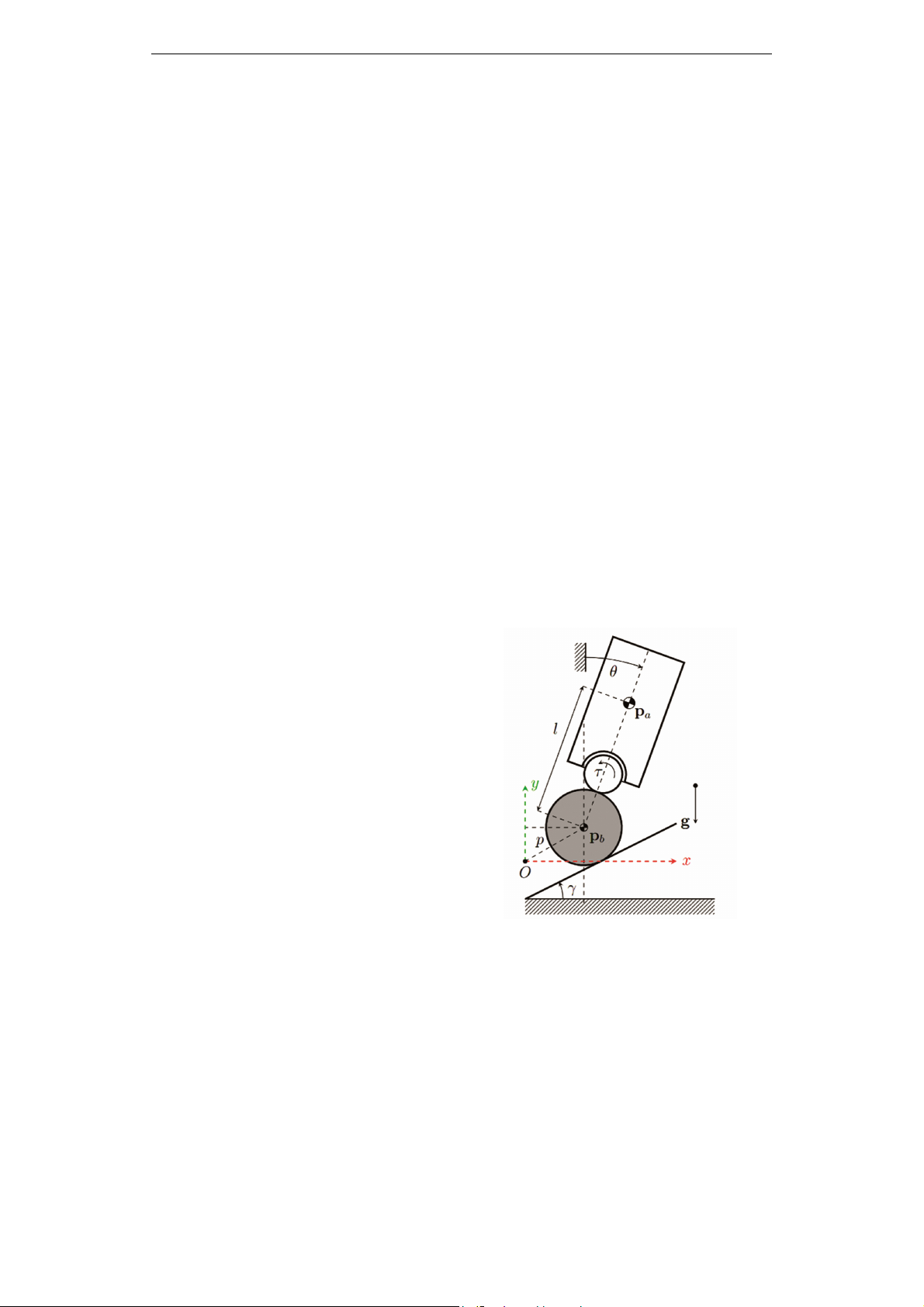
Hình 1. Mô hình của ballbot di chuyển
trên mặt phẳng nghiêng
Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
337
Phương trình mô hình toán học của
Ballbot được biến đổi từ phương trình Euler-
Lagrange có dạng:
qq qqq q

M( ) +C( , ) + G( ) = Jτ (1)
với:

;pp



qq
;






1
11 12 12
21 22 2
g
mm 0c
M= , C= , G=
mm 00 g
2
b c cc cbc
11 a b
224 4
bbb b
J J Jr Jrr
m= +4 + +4 +m+m
rrr r ;
cc
12 21 a
cb
JJ
m=m=-2 - +lmcos(+)
rr ;

2
2b
22 a a c 12 a
2
c
r
m =m l +J +J ,c =-lm sin( + )
r;
.
1ab2a
g
=
g
sin( )(m + m ),
g
=-
g
lm sin( )
Nhận xét: Sự khác biệt lớn nhất khi
Ballbot ổn định trên mặt phẳng nghiêng 0
so với khi ổn định trên mặt phẳng ngang
chính là góc nghiêng của thân ballbot
θvà
momen bánh xe giữ cho ballbot đứng được
trên dốc
τlà khác 0, giải phương trình (1) tìm
được:
θ,
τvới
q=0và 
q=0
3
bab
ac b c
r sin( )(m + m )
sin( ) = lm r (2r + r ) (2)
2
bab
bc
rsin( )(m +m )
τ=- 2r + r (3)
3. THIẾT KẾ BỘ ĐIỀU KHIỂN
Mục tiêu điều khiển đặt ra là Ballbot di
chuyển từ p đến vị trí đặt pd mà vẫn đảm bảo
góc nghiêng
hội tụ về d
(
d là góc lệch
thân đặt)
Hai mặt trượt được thiết lập với cho vị trí là
s1 và cho góc lệch thân là s2. Với mặt trượt
tầng đầu tiên, bằng cách xem xét tính ổn định,
luật điều khiển cho mặt trượt này được tổng
hợp từ hai phần: luật điều khiển tương đương
eq1 và luật điều khiển chuyển đổi
sw1. Luật
điều khiển tương đương giữ cho hệ thống bám
theo miền trượt ổn định và được suy ra từ điều
kiện 10s
, trong khi luật chuyển đổi sẽ đẩy hệ
về phía mặt trượt ổn định theo phương vuông
góc, đảm bảo hệ thống hội tụ cho dù có sự
xuất hiện của thành phần bất định hay nhiễu:
111
111
1
11 1 1
1
()()()
sgn( )
d
eq sw
kkpkkpp
ss




ΓM Cq G
ΓM J
ΓM J
(4)
Mặt trượt tầng thứ hai được tạo từ mặt
trượt s1 và mặt trượt s2 như sau:
12
s
ss
(5)
Với mặt trượt s
2 có luật điều khiển được
tính tương tự như mặt trượt s1:
1
22
222 1
22 2 2
1
()
sgn( )
ΘM Cq G
ΘM J
ΘM J



eq sw
ke
ss


(6)
Với việc chọn
=
1 =
2, chúng ta có luật
điều khiển tổng quát từ (4) và (6) như sau:
1
1
11
1
22
11
(( )(1) ( ))
(( )) sgn()
r
kkpkkpp
ke s s








ΓM Cq G
ΓM J ΘM J
ΘM Cq G
ΓM J ΘM J
(7)
trong đó:
1,
1,
2,
2,
,
, k1, k2, k là hằng
số dương và 10
Γ, 01

Θ.
Dựa vào Bổ đề Barbalat để chứng minh
rằng mô hình 2D của Ballbot mô tả theo
phương trình (1) di chuyển trên mặt phẳng
nghiêng nếu được điều khiển bởi luật điều
khiển (7) thì cả 2 mặt trượt 1
s
và 2
s
đều sẽ ổn
định tiệm cận, hay nói cách khác mặt trượt
tổng là ổn định tiệm cận [5].
4. ĐIỀU KHIỂN BALLBOT DI CHUYỂN
LÊN, XUỐNG DỐC
Tác giả đã thực hiện mô phỏng cho Ballbot
di chuyển trên mặt phẳng nghiêng 20 bằng
phần mềm MATLAB với các tham số vật lý
sau: Khối lượng phần thân ma = 3.2 kg; khối
lượng quả bóng mb = 0.62 kg; khối lượng
bánh xe mc = 0.2 kg; bán kính quả bóng rb =
0.12 m; bán kính bánh xe rc = 0.05 m; mô
men quán tính của phần thân a
J: 0.02 kg.m2;
mô men quán tính của quả bóng b
J= 0.00446
kg.m2; mô men xoắn của bánh xe đa hướng
c
J: 0.002 kg.m2; khoảng cách từ tâm quả
bóng đến trọng tâm phần thân l = 0.35m, và
gia tốc trọng trường g= 9.81m/s2.
Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
338
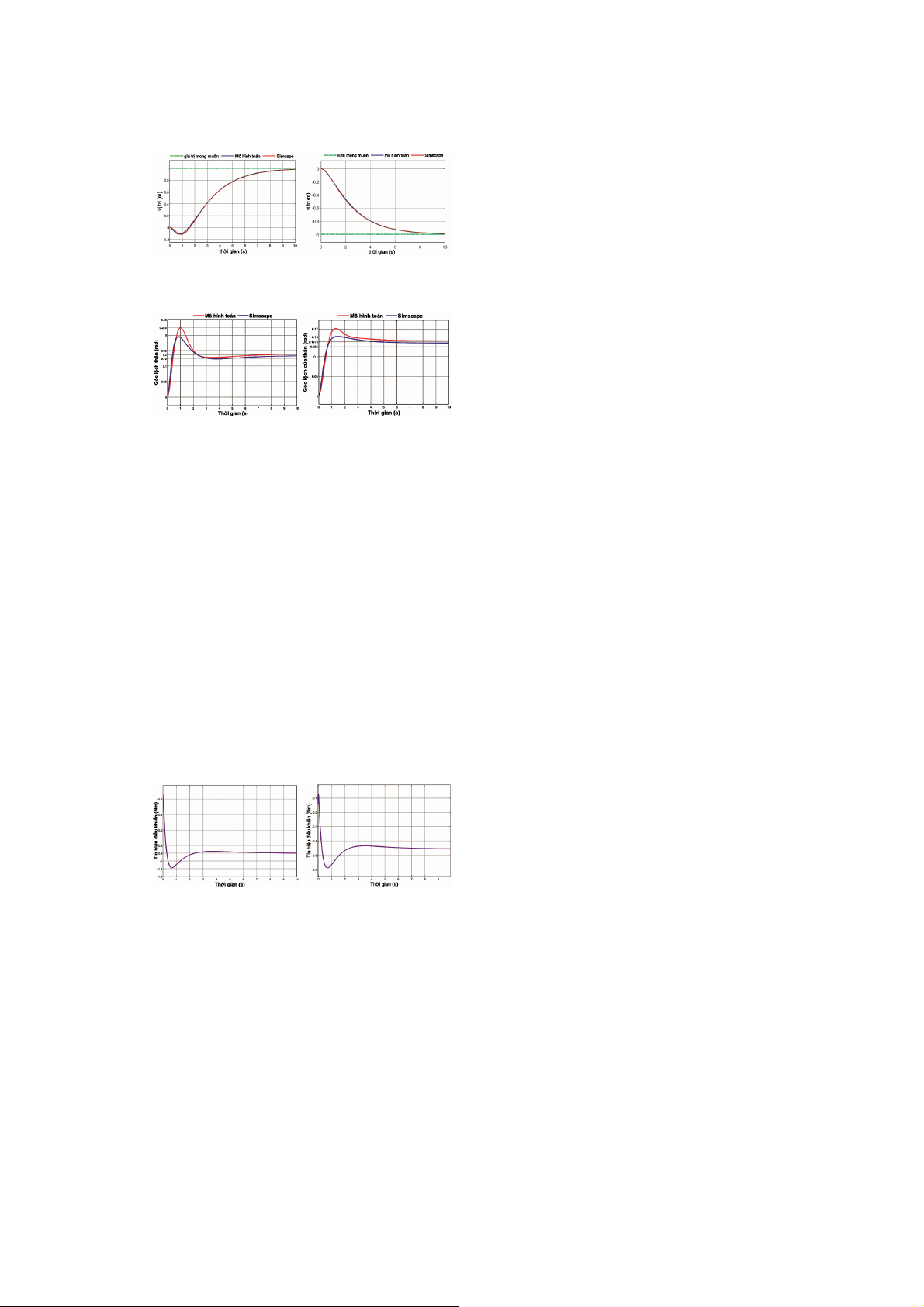
Kết quả mô phỏng ở hình 2 và 3 có so
sánh giữa việc dùng SMSs để điều khiển mô
hình toán học của ballbot và điều khiển mô
hình ballbot trên Simscape.
Hình 2. Vị trí Ballbot di chuyển lên dốc
và xuống dốc nghiêng 20
Hình 3. Góc lệch của thân Ballbot
khi di chuyển lên và xuống dốc nghiêng 20
Có thể thấy các đáp ứng đầu ra từ mô hình
Simscape và mô hình toán có cùng xu hướng
thay đổi và khá khớp với nhau.Tuy nhiên với
góc lệch thân thì mô hình Simscape cho đáp
ứng tốt hơn. Các mô phỏng ở hình 2 cũng
cho thấy hiệu quả của bộ điều khiển SMSs
khi đảm bảo tính ổn định và hội tụ về đúng vị
trí mong muốn. Quan sát hình 3 ta thấy rằng,
để Ballbot có thể đứng yên trên dốc, góc
nghiêng của thân phải được thay đổi (11 khi
lên dốc và 7.9 khi xuống dốc) để giữ cho
trọng tâm thân nằm ngay bên trên điểm tiếp
xúc giữa bóng và mặt nghiêng. Mặt khác,
khi cân bằng, momen của cơ cấu truyền động
luôn phải giữ khác 0 (hình 4) để chống lại thế
năng trọng trường của Ballbot.
Hình 4. Tín hiệu điều khiển Ballbot
khi di chuyển lên và xuống dốc nghiêng 20
5. KẾT LUẬN
Đóng góp ở nghiên cứu này của tác giả là
đã phát triển mô hình toán học và thiết kế bộ
điều khiển chế độ trượt SMSs cho hệ thống
Ballbot di chuyển trên mặt phẳng nghiêng.
Bằng cách so sánh mô hình toán học với mô
hình bán vật lý trên Simscape, nghiên cứu đã
chứng minh tính hợp lý và khả thi của mô
hình tính toán khi áp dụng trong thực tế để
thiết kế bộ điều khiển. Hơn nữa, các đáp ứng
đầu ra thu được từ hệ thống cho thấy phương
pháp trượt tầng có hiệu quả cao trong việc
đảm bảo hệ thống ổn định, cân bằng và di
chuyển về đúng vị trí mong muốn.
6. TÀI LIỆU THAM KHẢO
[1] M. Kumagai and T. Ochiai, “Development
of a robot balanced on a ball-Application of
passive motion to transport,” in 2009 IEEE
International Conference on Robotics and
Automation, 2009, pp. 4106-4111. doi:
10.1109/ROBOT.2009.5152324.
[2] P. Fankhauser and C. Gwerder, “Modeling
and Control of a Ballbot,” 2010.
[3] D. B. Pham and S.-G. Lee, “Aggregated
hierarchical sliding mode control for a
spatial ridable ballbot,” International Journal
of Precision Engineering and Manufacturing,
vol. 19, pp. 1291-1302, 2018.
[4] R. P. Mauro, S. Correlatore, S. Pastorelli, I.
Paolo, M. Melchiorre, and J. P. Chevalie,
“Preliminary study for the design of a
Ballbot,” 2018.
[5] Vu DC, Pham MD, Nguyen TTH, Nguyen
TVA, Nguyen TL. “Time-optimal trajectory
generation and observer-based hierarchical
sliding mode control for ballbots with
system constraints”. Int J Robust Nonlinear
Control. 2024; 34(11): 7580-7610. doi:
10.1002/rnc.7358.