Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
57
MÔ HÌNH HÓA VÀ ĐIỀU KHIỂN BÁM QUỸ ĐẠO
QUADROTOR SỬ DỤNG BỘ ĐIỀU KHIỂN TRƯỢT
Nguyễn Huy Thế, Nguyễn Văn Ninh
Trường Đại học Thủy lợi, email: nguyenhuythe@tlu.edu.vn
1. GIỚI THIỆU CHUNG
Trong những năm gần đây, với sự phát triển
nhanh chóng của công nghệ đã cho ra đời
nhiều dạng thiết bị bay không người lái, trong
đó dạng quadrotor sử dụng bốn cánh quạt (viết
tắt QUAV). Với khả năng cất cánh và hạ cánh
thẳng đứng, cùng khả năng điều hướng linh
hoạt trong mọi loại địa hình, QUAV đã thu hút
sự quan tâm lớn từ cộng đồng nghiên cứu do
chúng có thể ứng dụng vào vào nhiều lĩnh vực
trong cuộc sống như nông nghiệp, quân sự,
cứu hộ cứu nạn, logistics [1]. QUAV là một hệ
có tính phi tuyến cao, hụt cơ cấu chấp hành
cùng với sự xen kênh của các thông số, bởi hệ
có 6 biến cần điều khiển trong đó chỉ có 4 cơ
cấu chấp hành. Do đó, để cải thiện hiệu suất và
sự ổn định của hệ, các bộ điều khiển đã được
đề xuất để giải quyết các vấn đề trên.
Với ưu điểm chống nhiễu và ổn định tốt,
bộ điều khiển trượt (SMC) có khả năng điều
chỉnh linh hoạt và chính xác, giúp nâng cao
khả năng ổn định của QUAV đối với các tác
nhân từ môi trường bên ngoài. Bài báo này
tập trung vào nghiên cứu mô hình động lực
học của QUAV và đề xuất bộ điều khiển
trượt trong việc điều khiển bám quỹ đạo,
đồng thời đánh giá kết quả mà phương pháp
này đạt được.
2. PHƯƠNG PHÁP NGHIÊN CỨU
2.1. Mô hình hóa
Mô hình QUAV mô tả trong Hình 1 bao
gồm 4 động cơ gắn với 4 cánh quạt được đặt
chéo nhau. Chuyển động của QUAV được
điều khiển bằng cách điều chỉnh tốc độ quay
của các động cơ.
Hình 1. Mô hình QUAV [2]
Mô hình QUAV được xét trong hai hệ tọa
độ gồm hệ tọa độ cố định E (Oe, ex, ey, ez) và
hệ tọa độ động gắn tại trọng tâm của QUAV
B (Ob, bx, by, bz). Các tọa độ suy rộng xác
định hướng của QUAV là các góc
(roll),
(pitch) và
(yaw). Ta có ma trận chuyển
đổi giữa hai hệ tọa độ:
E
B
R
cc cs ssc ss csc
cs cc sss sc css
ssc cc





(1)
trong đó c
= cos
; s
= sin
. Vận tốc góc
trong hệ tọa độ cố định

T
BpqrW liên
hệ với vận tốc góc trong hệ tọa độ động:
10
0
0
ps
qcsc
rscc







(2)
Phương trình chuyển động của QUAV
trong không gian [2]:

gc
gry c B B B
P F-F -F
M+M -M =I W +W W

m
(3)
Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
58
Đặt


-- ,
1gc
1
P,Q = F F
F
m

2
2
2
2
FQ



yy zz c
xx xx xx
zz xx c
yy yy yy
xx yy cy
zz zz
II k
J
III
II k
J
III
II k
II














, có thể
biến đổi hệ phương trình (3) trở thành:
1
-1
2
F
P= +F
Q=I M+F


m
(4)
trong đó, trọng lực

T
00mg
g
F, lực cản
T
cx cy cz
kx ky kz
c
F

, vị trí của QUAV
trong hệ tọa độ cố định

T
x
yzP, các góc
quay
T
Q

, mômen con quay hồi
chuyển
T
ΩΩ0Jp q
gry
M
, mômen cản
T
22 2
ccc
kkk
c
M




 và mômen quán tính
diag , ,
xx yy zz
IIII . Đặt tổng lực nâng từ bốn
động cơ là
2222
11234t
Ukwwww
, với t
klà
hệ số tác động lên rotor, i
w là tốc độ của mỗi
động cơ. Tổng hợp lực tác động lên QUAV là:
E
B1
00FR T
U (5)
2.2. Thiết kế bộ điều khiển trượt
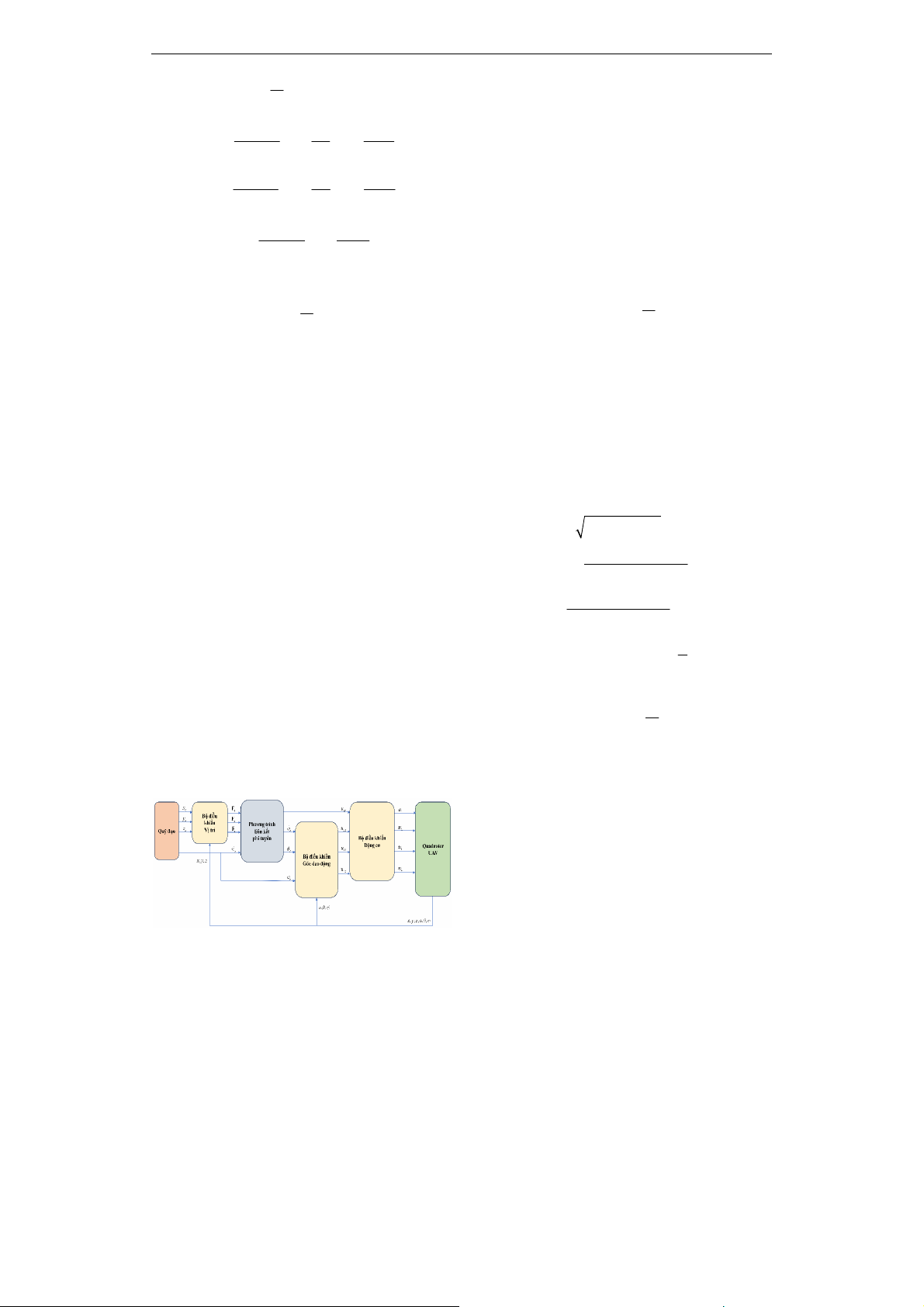
Bài toán điều khiển QUAV với trọng tâm
chuyển động theo quỹ đạo mong muốn được
thực hiện theo sơ đồ mô tả trong Hình 2.
Hình 2. Cấu trúc bộ điều khiển QUAV
2.2.1. Thiết kế bộ điều khiển vị trí
Để điều khiển QUAV theo quỹ đạo đặt
trước
T
ddd
x
yz
d
Pvà d
. Các véctơ sai
lệch bám quỹ đạo được định nghĩa như sau:
;
1d
e=P P
.
1d
e=P P

Xét mặt trượt:
1111
s=ce+e
(6)
Với c1 = diag(cx, cy, cz) là tham số của bộ
điều khiển. Từ phương trình (4) và (6) thu
được:

111111d 1
1
s =ce e =ce P F+ F

 m
m
 (7)
Áp dụng bộ điều khiển trượt dựa trên luật
cấp số nhân:
sat.
11 111
s= n s ks

(8)
với n1 = diag(nx, ny, nz), k1 = diag(kx, ky, kz) là
các tham số điều khiển. Sau một vài phép biến
đổi toán học thu được tín hiệu điều khiển:
.sat
1d111 1 11
eF= F +P +c +n s +ks

m (9)
Kết hợp phương trình (9) và (5) thu được:
222
1
cos sin
arctan
sin cos
arctan cos
xyz
xy
d
z
xy
dd
z
UFFF
FF
F
FF
F









(10)
Chọn hàm Lyanpunov 2
1
1
2
V1
s. Lấy đạo
hàm theo thời gian thu được:

1.Vm
m
11 d 111 1
1
ss s ce P F+ F


Do V1 = s1.n1sign(s1) 0 nên hệ ổn định [2].
2.2.2. Thiết kế bộ điều khiển góc quay
Để điều khiển các góc quay của QUAV,
một vòng điều khiển bên trong được thiết kế
dựa trên SMC tương tự như vòng điều khiển
vị trí:
.sat
2d222 2 22
eM=I F +Q +c +n s +k s
(11)
với c2 = diag(c
, c
, c
), n2 = diag(n
, n
, n
),
k2 = diag(k
, k
, k
) là các tham số của bộ
điều khiển.
Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
59
3. KẾT QUẢ NGHIÊN CỨU
Xét QUAV với các tham số mô hình như
Bảng 1 chuyển động với quỹ đạo cho trước:
x = sin(5t); y = sin(5t +
/2); z = 0.05x + 1.
Bảng 1. Tham số của mô hình QUAV
Tham số Giá trị Tham số Giá trị
m (kg) 1.8 J (kg.m2) 7.2 106
g (m/s2) 9.81 kc
(N/m/s) 7.2 106
Ixx (kg.m2) 1.7 102 kc
(N/m/s) 7.2 106
Iyy (kg.m2) 1.7 102 kc
(N/m/s) 7.2 106
Izz (kg.m2) 2.8 102 kt (Nm/A) 4.3 106
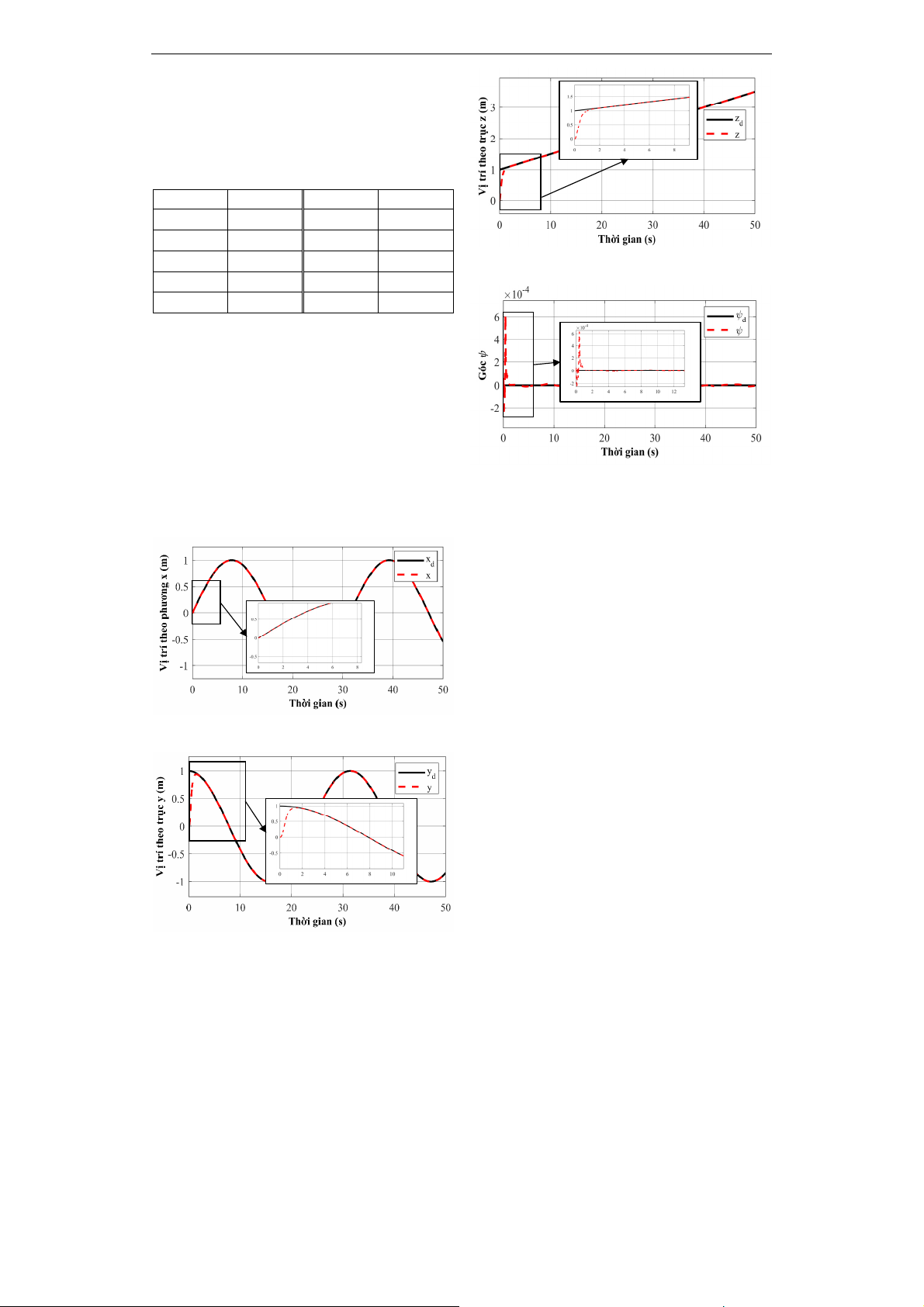
Kết quả áp dụng bộ điều khiển trượt vào
mô hình QUAV nêu trên được thể hiện trong
các hình vẽ dưới đây. Hình 3 biểu diễn vị trí
của QUAV theo phương x, bộ điều khiển
nhanh chóng bám quỹ đạo đặt. Trong các
Hình 4 và Hình 5, đáp ứng vị trí của QUAV
theo phương y và phương z lần lượt cũng
bám quỹ đạo đặt sau thời gian khoảng 2 s.
Hình 6 biểu diễn đáp ứng của góc quay yaw
của QUAV, giá trị dao động bé rồi nhanh
chóng dao động ổn định quanh góc 0.
Hình 3. Vị trí của QUAV theo trục x
Hình 4. Vị trí của QUAV theo trục y
Hình 5. Vị trí của QUAV theo trục z
Hình 6. Góc quay yaw của QUAV
4. KẾT LUẬN
Bài báo đã trình bày về mô hình động lực
học của thiết bị bay không người lái bốn cánh
quạt, có xét đến ảnh hưởng của lực cản từ môi
trường. Từ đó, đề xuất bộ điều khiển trượt để
áp dụng giải quyết bài toán điều khiển QUAV
chuyển động theo quỹ đạo mong muốn. Kết
quả mô phỏng hệ thống điều khiển cho thấy
bộ điều khiển trượt đã đề xuất rất hiệu quả cả
trong điều khiển vị trí và hướng của QUAV,
giúp QUAV hoạt động ổn định.
5. TÀI LIỆU THAM KHẢO
[1] S. Ahirwar, R. Swarnkar, S. Bhukya, and G.
Namwade. 2019. Application of Drone in
Agriculture. Int. J. Curr. Microbiol. Appl.
Sci., vol. 8, no. 01, pp. 2500-2505, Jan. 2019.
[2] M. Labbadi, Y. Boukal, and M. Cherkaoui.
2022. Advanced Robust Nonlinear Control
Approaches for Quadrotor Unmanned
Aerial Vehicle, vol. 384.