
Journal of Engineering Research 13 (2025) 68–83
Available online 18 September 2023
2307-1877/© 2023 The Author(s). Published by Elsevier B.V. on behalf of Kuwait University. This is an open access article under the CC BY-NC-ND license
(http://creativecommons.org/licenses/by-nc-nd/4.0/).
Quadruple spherical tank systems with automatic level control applications
using fuzzy deep neural sliding mode FOPID controller
Ashwini A
a
,
*
, S.R. Sriram
b
, Joel livin A
c
a
Department of ECE, Vel Tech Rangarajan Dr. Sagunthala R&D Institute of Science and Technology, Chennai, India
b
Department of ECE, College of Engineering, Guindy, Anna University, Chennai, India
c
University of Technology and Applied Science, Ibra, Oman
ARTICLE INFO
Keywords:
FOMCON toolbox
MATLAB/Simulink
Non- linear quadruple spherical tank systems
Proposed fuzzy deep neural sliding mode
fractional order proportional integral
derivative
Real-time liquid level control
ABSTRACT
The premier goal of this research is to develop the Fuzzy Deep Neural Sliding Mode Fractional Order Proportional
Integral Derivative (FDN-SM-FOPID) controller system for controlling liquid in quadruple spherical tank systems.
This is used in non-linear spherical systems to control the level of liquid in real time. These models’ dynamics
allow for a more accurate identification of the spherical tank system that generates control signals from liquid
samples obtained at reference levels. However, because the system is susceptible to outside disturbances, error
minimization is not done. Therefore, it requires the addition of a special controller to lessen this flaw. The
suggested Deep Neural Fuzzy model’s six-layered network is optimized using the back-propagation method. As a
result, the system’s efficient training reduces offset model errors, steady state errors, and unmeasured distur-
bances. The liquid level is maintained and controlled by this neural intelligence system, which meets the
necessary design requirements such as no overshoot, time constant, less settling and rise time, which is used in
various platforms. The FOMCON toolbox in MATLAB software is used for research simulation work. The
chemical industry, wastewater treatment, the aerospace industry, and the pharmaceutical industry have all
employed the suggested quadruple spherical tank system to test its practicality. The experimental and simulation
results are demonstrated by a real-time liquid control experimental setup.
Introduction
Numerous applications can be found in the petrochemical, paper-
making, pharmaceutical, and effluent water treatment industries.
Maintaining the liquid level in tanks is of the utmost importance for
industries. The standard PID controlling system can successfully tune in
either time or frequency in order to achieve the necessary criteria [1].
Neural controllers are used in numerous sectors for autonomous liquid
level management. If the challenges of the task are well understood, then
there can be a successful implementation of the neural network [2].
Many of the existing research work focus on techniques for level
control in tanks, such as PID with back-stepping controller [3], feed
forward compensator [4], linearized controller with feedback [5], and
machine learning systems [6]. However, prior understanding of the
levelling system is required in these systems, which finds the major
drawback. Pipes, tanks, valves, pumps, and sensors are components of a
general tank system. During the control of these components, the liquid
type with the aperture can change, leading to faults in system analysis.
This causes non-linear characteristics of the spherical tank systems. As a
result, framing an appropriate mathematical system model is found to be
challenging.
A sliding mode controller using a parameter estimator more precisely
on higher order values was developed by Chaudhari et al. [7]. Thus, it is
important to find a technique to deal with non-linear property estima-
tion of the measured level of signal. Shah et al. proposed a sliding mode
system with non-switching characteristics to compensate for the delay in
the quadruple-based tank system [8]. Overall, the four regions have a
0.4 % overshoot and a 1.9 % undershoot. This increases the conver-
gence’s speed. Son et al. designed the adaptive inverse evolutionary
based neural controller. This hybrid control system [9] combines feed
forward and PID techniques. The chattering attenuation is controlled by
a twisting algorithm as suggested by Gurjar et al. [10]. The sliding mode
system is more advantageous when compared to the feedback linariza-
tion algorithm [11]. Bououden et al. [12], proposed a fuzzy model with
ant colony optimization. The discovery of non-linear parameter pro-
cessing is the key benefit. Yu et al. [13] suggested a system with fuzzy
iterative control for fault-tolerant non-linear systems.
* Corresponding author.
E-mail address: a.aswiniur@gmail.com (A. A).
Contents lists available at ScienceDirect
Journal of Engineering Research
journal homepage: www.journals.elsevier.com/journal-of-engineering-research
https://doi.org/10.1016/j.jer.2023.09.022
Received 23 June 2023; Received in revised form 14 September 2023; Accepted 17 September 2023
Journal of Engineering Research 13 (2025) 68–83
69
Thamallah et al. [14] suggested Takagi-Sugeno fuzzy systems, which
employ particle swarm approaches to optimize a quadruple tank. Çetin
et al. [15] proposed a neural model with a predictive mechanism that
approximates and regulates the functional parametric values. These
models aid in the discovery of nonlinear black box soft computing
methodologies that aid information for designing these systems.
Research work has been put forth that use type-1 fuzzy [16], CMAC
[17], recurrent neural fuzzy [18] and fuzzy type-2 [19] systems to boost
control due to feedback learning errors.
Numerous EAs, including WOA [20], ACO [21], and others, are
combined with neural network systems for identification. Evolutionary
algorithms (EA), which aid in the training of neural networking systems,
achieve global optimality. To increase the accuracy of predictions, the
gradient entropy with machine learning system has been created
[22–24]. Numerous recent studies have integrated and changed the
traditional strategies which solve these challenging situations. The
neural network based on hybrid GA-PSO system approaches was used to
train the forecast for power demand was suggested by Nguyen et al.
[25]. The Differential Evolution method discovers its beneficial fact in
obtaining global optimized standards, despite its initial value of pa-
rameters. In [26], [27], a back propagation DE system was proposed.
Anand et al. [28] created a modified DE for recognizing a redundant
manipulator with a 3, 4-DoF adaptive network based on an automated
Nomenclature
Ll Liquid level in lower tank
SPpj Pump speed
Gp Pump gain
Fi Flow of liquid in upper tank
Dp Derivative model
Ip Integral model
CSoi Curved Surface Area of the spherical outlet
CSui Curved Surface Area of upper spherical tank
Nc2 Noise: valve 2
Nc4 Noise: valve 4
v1, v2 Pump speed rating
ΔSpp, ΔSpD Scaling factors
ER Error
Tf(e)Controller transfer function
vp1(k), vp2(k)Voltages - pump 1 and 2
o(s)System output
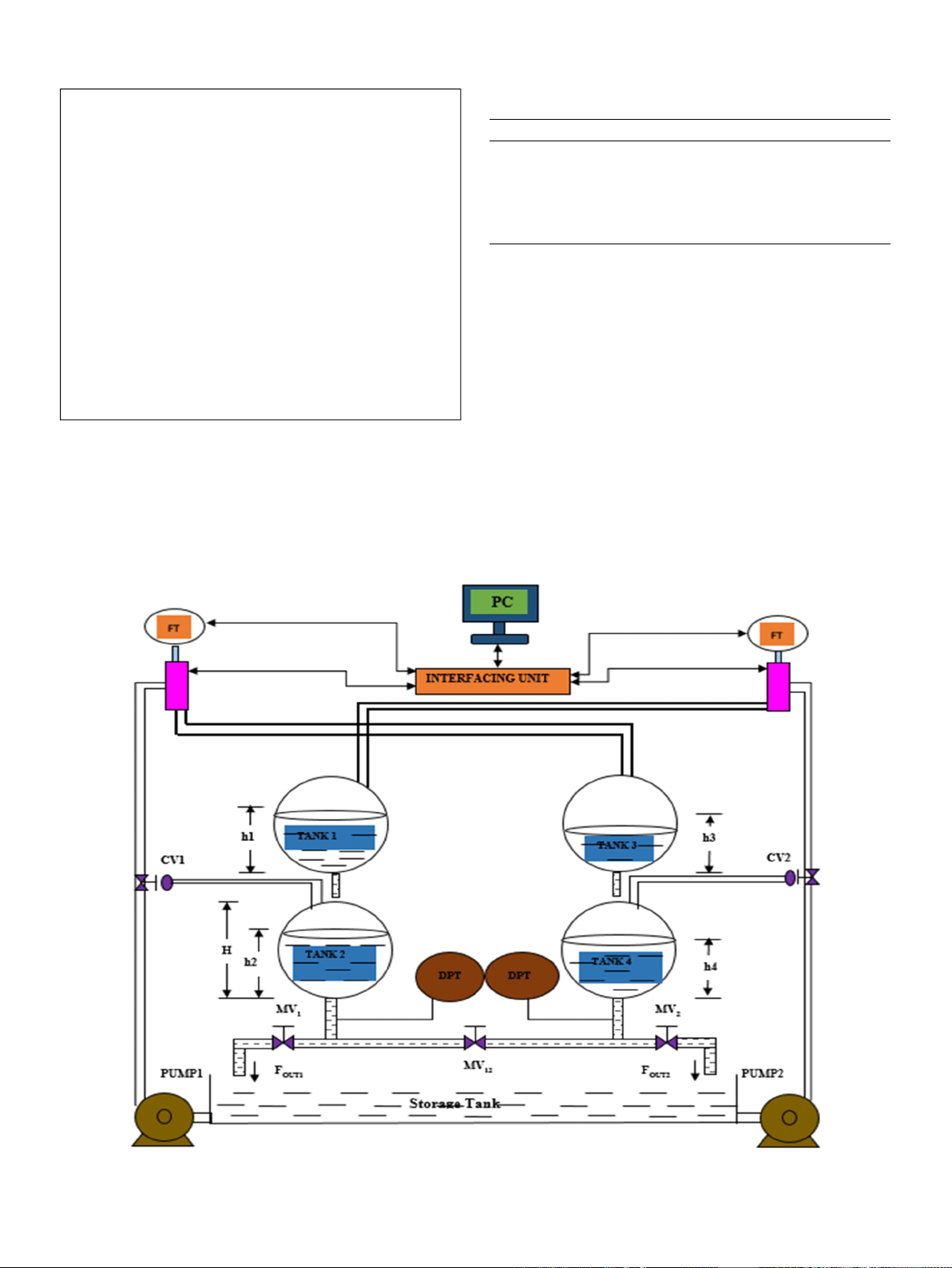
Fig. 1. Model of four-spherical tank system.
Table 1
Spherical tank - specifications.
Parameter Range Unit
CSo1, CSo2, CSo3, CSo4 4.6 cm
2
Spherical tank: Diameter 50 cm
CSt1, CSt3 0.9 cm
2
CSt2, CSt4 0.67 cm
2
Maximum inflow 106.83 cm
3
/s
Spherical tank: Height 50 cm
Gain, Gkp 6.8 -
A. A et al.
Journal of Engineering Research 13 (2025) 68–83
70
system [29,30]. A deep learning algorithm is used to tune the PID
controller, which also successfully controls speed [31,32].
The microgrid responses are investigated by individually linking
each renewable energy source to the biogas generator, which observes
an increase in fluctuations in penetration. Jegatheesh et al. [33] created
a brand-new Fuzzy FOPID controller for regulating the liquid level. This
is developed to manage spherical tank liquid through a fractional order
system. The features of a perceptron network are optimized using uni-
fied multiple particle swarm optimization to produce results that are
nearly optimal, and the optimized network subsequently selects the
parameters of a fuzzy system. Utilizing a unique swarm algorithm with
PID controller with redox flow battery (RFB) provides a realistic power
system’s frequency [34]. The DCNN controlling method tracks robotic
manipulators by a fractional-order system. Switching gain is signifi-
cantly lower. The performance of stiff robotic manipulator control is
improved while chattering phenomena are decreased when DCNN and
FOTSM are combined. The singularity problem avoids differentiating
the exponential terms [35]. Adding a biodiesel generator also signifi-
cantly lowers frequency variations in the system [36]. A controller with
cascade system was developed to effectively increase AGC with wind,
fuel and solar cells. The competitive algorithm works well for optimizing
the controller settings [37]. [38] suggests an artificial neural network.
DFIG thermal turbines connected through transmission lines are
considered for the analysis.
Research gap identified
1. The non-linear spherical tank systems are highly non-linear in
nature, as in [39]. Thus, modelling, analyzing and controlling these
non-linear systems requires advanced and sophisticated control
algorithms.
2. A real-time FOPID controller creates chattering problems due to
the non-linear mechanism [40]. Though FOPID controllers offer benefits
in handling non-linear systems, careful tuning is necessary to prevent
chattering issues in real-time applications.
3. Control strategies developed for specific operating conditions
might not generalize well to different scenarios due to the non-linear
nature of the system. This can lead to reduced adaptability and robust-
ness [43].
3. Fuzzy-based systems, which make up the majority of intelligent
systems, can successfully regulate liquid levels. While most of the
existing solutions fail to do so, the time domain specifications are
controlled with fuzzy SMC-based FOPID controllers [41].
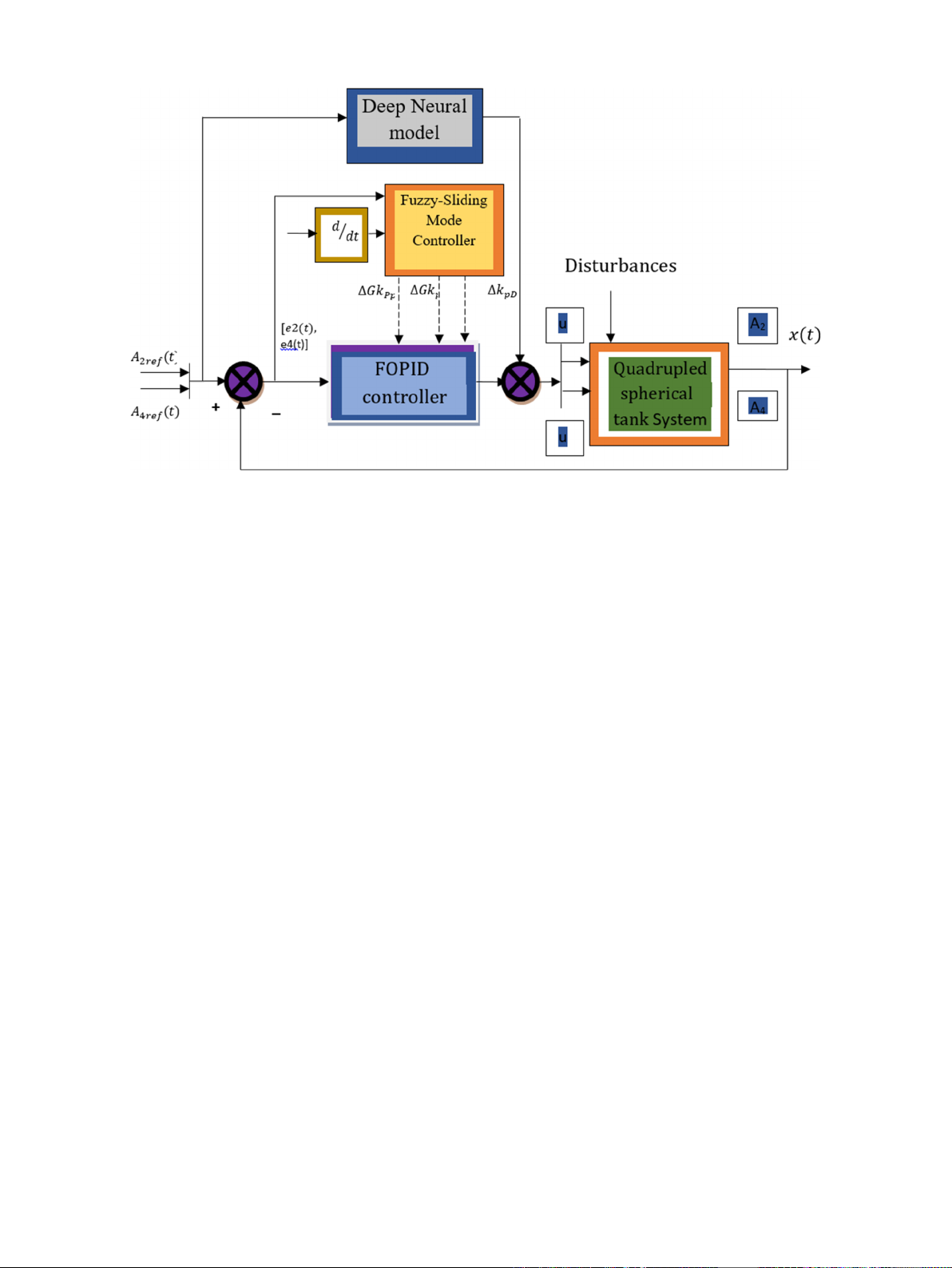
Merits of proposed work
Fuzzy Deep Neural Sliding Mode Fractional Order Proportional In-
tegral Derivative (FDN-SM-FOPID) is proposed for liquid level control in
a quadruple spherical tank system. This research work effectively ad-
dresses a number of issues.
•The key advantage of combining the proposed SM-FOPID with a deep
fuzzy neural networking system is that it enables real-time liquid
level management with improved performance and positive time
domain functional properties.
•A sliding mode governing mechanism was created with the goal of
generating a nonlinear system uncertainties in the presence of
disruptions.
•The six-layered network framework uses back propagation methods
that work on proposed deep neural networks. By lowering offset
errors, unmeasured disturbances, and steady state errors, the system
is trained.
•For a successful demonstration of this sophisticated method, set
point tracking of performance to sustain the set point values during
the occurrence of an external disturbance is explored. Additionally,
errors are bound and minimized by the proposed research work.
•For the proposed controller, real-time experimental tests were con-
ducted to assess how well they managed the spherical tank liquid
level. The impact of a series of set point adjustments is evaluated, and
the reaction to both positive and negative load disturbances is noted.
Fig. 2. Flow of FDN-SM-FOPID controller.
A. A et al.

Journal of Engineering Research 13 (2025) 68–83
71
Additionally, tests are run to ascertain how well the controllers
operate when set point changes and also during the presence of load
disturbances.
•To assess the effectiveness and viability of the proposed FDN-SM-
FOPID controller, simulation and real-time control data are shown.
Paper organization
Section 2 gives a quadruple spherical tank system in its physical
mode. Section 3 introduces the proposed FDN-SM-FOPID controller to
control the liquid level. Simulation is performed in Section 4 with real-
time experimental results. The conclusion is found in Section 5.
Quadruple tank spherical system- mathematical model
A nonlinear tank system with significant strong coupling character-
istics and time delay is given in Fig. 1. A lower tank liquidity level is
given as Ll, CSoi is the surface area of outflow in the lower tank system.
The upper tank system with surface area and flow are given by CSuiand Fi
respectively. Both the above terms allows for precise regulation of the
liquid supply to the downstream process. The pressure generated by the
elevated upper tank creates a potential energy difference, which drives
the flow of liquid. The pump speed is given by Spj. The control valves for
noise are given by Nc2 andNc4. One of the prime difficulties in the pro-
cessing industries is level based control in an interconnected spherical
tank system. This is nonlinear in nature due to the change in radius of
the tank system.
The spherical tank’s radius changes from top to bottom. The process
is carried out in spherical tanks with a radius of 25 cm and height of
50 cm respectively. The differential Eqs. (1–4) with mass balance de-
scribes this linearization around the operating point as follows.
Tank 1 Model :
∂
L1(t)
∂
t=1
CSo1[(1−N1)Sp1v1(t) − CSu1
2gL1(t)
√(1)
Tank 2 Model :
∂
L2(t)
∂
t
=1
CSo2[N2Gp2vp2(t) + CSu2
2gL1(t)
√−CSu2
2gL2(t)
√](2)
Table 2
Regions- modelling parameters.
Region Flow Rate (cm
3
/s) h
1
(cm) h
2
(cm) h
3
(cm) h
4
(cm) CS
1
CS
2
CS
3
CS
4
R
1
R
2
R
3
R
4
τ
1
τ
2
τ
3
τ
4
1 0–25 1.713 1.692 1.597 1.768 1.5612 0.3934 1.4697 0.5972 0.0071 0.1763 0.0169 0.1256 2.4169 32.485 30.972 29.453
2 26–50 6.746 6.324 6.329 6.729 0.7694 0.1735 0.6581 0.1837 0.0159 0.1278 0.2491 0.2249 15.941 224.71 214.92 219.28
3 51–75 14.86 14.19 13.81 14.07 1.0371 0.1423 0.2837 0.3917 0.0217 0.3514 0.0376 0.2149 22.658 843.61 573.16 769.35
4 76–100 32.6 29.41 31.94 30.76 0.2998 0.0914 0.0318 0.119 0.0349 0.5179 0.5369 0.5462 62.942 103.59 1163.5 1049.4
Table 3
ΔGKp– Fuzzification rules.
er (k) Δer (k)
Nl Ns Nm Z Pm Ps Pl
Nl l l l l l l l
Ns s l s l l s s
Nm s l l l l l s
Z s s s l s s s
Pm s l l l l l s
Ps s l s l l s l
Pl l l l l l l s
Table 4
ΔGKd– Fuzzification rules.
er (k) Δer (k)
Nl Ns Nm Z Pm Ps Pl
Nl s s s s s s s
Ns l l l s l l l
Nm l s l s l s l
Z l l l l l l l
Pm l l l s l l l
Ps s s s s s s s
Pl l s l s l s l
A. A et al.
Journal of Engineering Research 13 (2025) 68–83
72
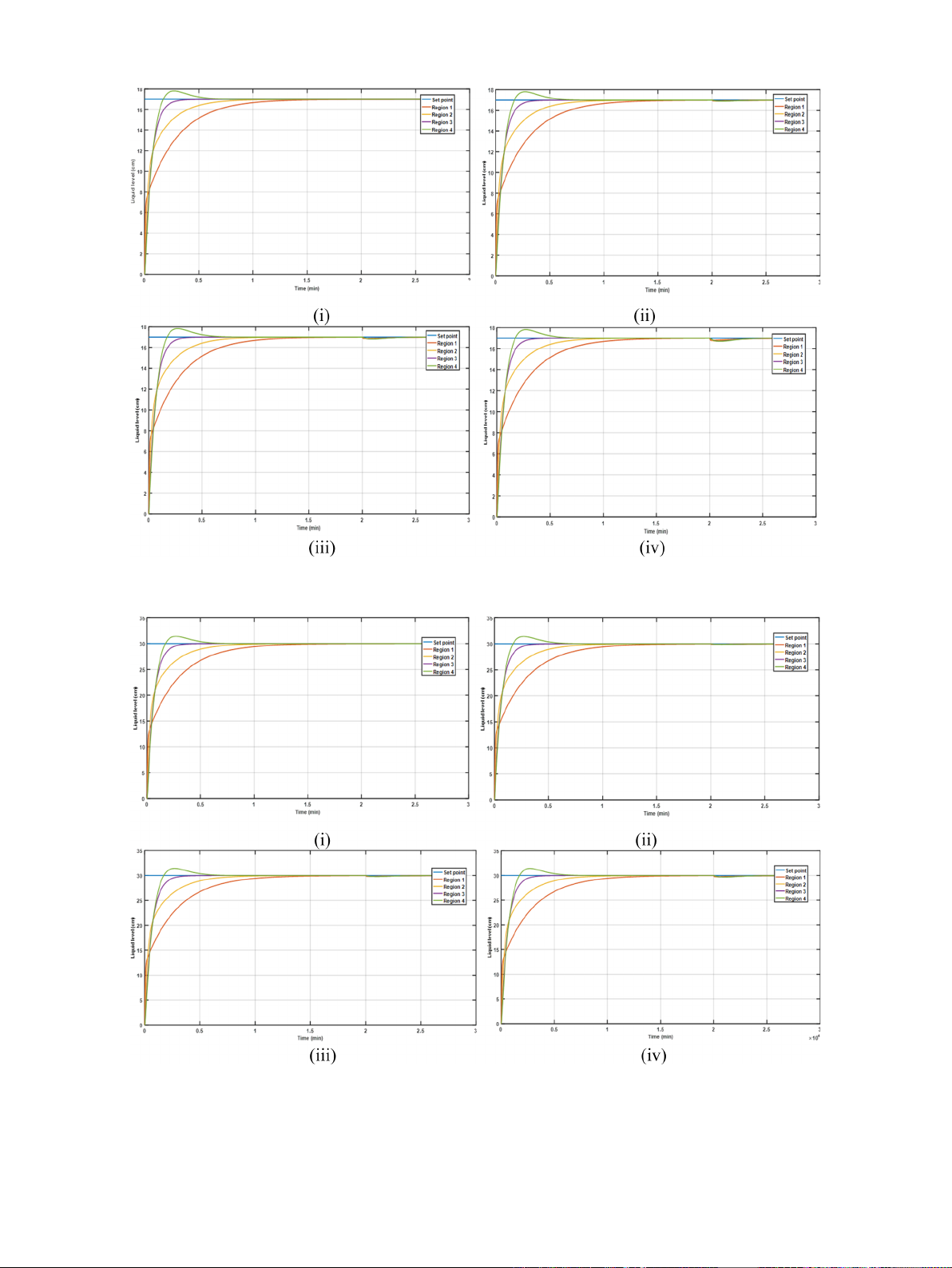
Fig. 3. Responses of four regions at SP=17, t =2 min (i) no disturbance; with disturbance (ii) 5 lph (iii) 10 lph (iv)15 lph.
Fig. 4. Responses of four regions at SP=30, t =2 min (i) no disturbance; with disturbance at (ii) 5 lph (iii) 10 lph (iv) 15 lph.
A. A et al.












![Đề cương đề tài nghiên cứu khoa học [chuẩn nhất/mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251117/duong297/135x160/26111763433948.jpg)













